et si f(x) g(x) - Maths au lycée Mezeray

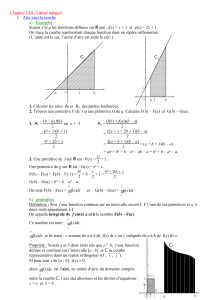
Intégrale d’une fonction sur un intervalle
I.
Calculs d’aires et primitives .
1. Activité préparatoire
la fonction représentée ci-contre est la fonction constante définie par
f(x) = 2
Donner l’aire de la partie grisée en fonction de a et b
S=
Trouver une fonction F telle que F’ = f .
F(x) =
Calculer 𝐹(𝑏) − 𝐹(𝑎)
𝐹(𝑏) − 𝐹(𝑎) =
la fonction représentée ci-contre est la fonction définie par
f(x) = x
Donner l’aire de la partie grisée en fonction de a et b
S=
Trouver une fonction F telle que F’ = f .
F(x) =
Calculer 𝐹(𝑏) − 𝐹(𝑎)
𝐹(𝑏) − 𝐹(𝑎) =
(𝑔𝑟𝑎𝑛𝑑𝑒 𝑏𝑎𝑠𝑒+𝑝𝑒𝑡𝑖𝑡𝑒 𝑏𝑎𝑠𝑒)×ℎ𝑎𝑢𝑡𝑒𝑢𝑟
 On rappelle que l’aire d’un trapèze est donnée par
2
la fonction représentée ci-contre est la fonction définie par
f(x) = −
1
3
x+3
Donner l’aire de la partie grisée en fonction de a et b
S=
Trouver une fonction F telle que F’ = f .
F(x) =
Calculer 𝐹(𝑏) − 𝐹(𝑎)
𝐹(𝑏) − 𝐹(𝑎) =
2. Généralisation :
Comment peut-on faire pour calculer l’aire grisée sachant que la courbe est
celle de la fonction définie par f(x) = x² ? Calculer cette aire S .
1
3. Propriété
Si f est une fonction continue et positive sur l’intervalle [a ;b]
Alors l’aire de la partie du plan délimitée par l’axe des abscisses , la courbe
représentative de f et les droites (verticales) d’équations x= a et x= b est
donnée par :
S = 𝑭(𝒃) − 𝑭(𝒂) unités d’aire ( u.a.)
Où F est une fonction dérivable sur [a ;b] telle que F’ = f
.L’unité d’aire étant le rectangle unité de cotés ‖𝑖⃗‖ et ‖𝑗⃗‖
4. Exercice 1
Soit f la fonction définie par f(x) = 𝑒 𝑥 + 1
On note (C) sa représentation graphique dans un repère orthonormé d’unité graphique 2 cm
Donner , en cm² , l’aire de la partie du plan délimitée par l’axe des abscisses , la courbe représentative de
f et les droites (verticales) d’équations x= -1 et x= 2
5. Exercice 2
Soit f la fonction définie par f(x) =
1
𝑥+2
On note (C) sa représentation graphique dans un repère orthonormé d’unité graphique 3 cm
Donner , en cm² , l’aire de la partie du plan délimitée par l’axe des abscisses , la courbe représentative de
f et les droites (verticales) d’équations x= 1 et x= e
I.
Primitives
1. Définition
Etant donnée une fonction f définie et continue sur un ouvert I , on appelle primitive de f sur I
toute fonction F dérivable sur I telle que F’ = f
2. Théorème (admis)
Si f est une fonction continue sur I alors elle admet des primitives sur I
3. Remarque :
Si F est une primitive de f sur l’ouvert I alors G = F + k (où k est un réel quelconque ) est aussi une
primitive de f sur I . ( en effet si F’ = f alors G’= F’ + 0 = f ). On dit :
Il y a une infinité de primitives d’une même fonction
Deux primitives d’une même fonction ne diffèrent que d’une constante k
Toute primitive de f a la forme F + k où F est une primitive particulière de f et k un nombre réel
Exemple :
Soit f définie par f(x) = 𝑥 3 – 3x + 4
1
1
Soit F définie par F(x) = 4 𝑥 4 – 3 × 2 x² + 4x est une primitive particulière de f sur IR ( car F’ = f
fastoche !!)
Donc , la forme générale des primitives de f sur IR est
1
4
𝐹𝑘 (x) = 𝑥 4 –
3
2
x² + 4x + k (k ∈ IR)
2
4. Primitive vérifiant une condition particulière
Parmi les primitives
sur particulière
I d’une même
f continue
sur I , illan’en
existe
seulek de la
La condition
F(𝑥0fonction
) = 𝑦0 permet
de déterminer
valeur
de laqu’une
constante
vérifiant
une
condition
particulière
du
type
F(𝒙
)
=
𝒚
(
𝒙
et
𝒚
connus
)
𝟎
𝟎
𝟎
𝟎
remarque précédente .
 Exemple :
Déterminer la primitive F sur IR de la fonction f définie par f(x) = 𝑥 3 – 3x + 4 qui vérifie F(1) = –1
1
4
On a vu ci-dessus que la forme générale des primitives de f sur IR est 𝐹𝑘 (x) = 𝑥 4 –
On veut F(1) = – 1 donc
1
4
14 –
3
2
1² + 4×1 + k = –1 ⇔ k =
1
La primitive cherchée est donc définie par F(x) = = 4 𝑥 4 –
3
2
x²
1
3
–1 – 4 + 2
25
+ 4x – 4 .
3
2
x² + 4x + k
–4 ⇔ k=–
25
4
5. Exercices :
Exercice 1
1. Montrer que la fonction F définie par
F(x) = Error! x3 – 3x² +1 est une primitive sur IR de la fonction f définie par f(x) = x² – 6 x
2. Déterminer la primitive G de f sur IR qui vérifie G(0) = 0
Exercice 2
1. Montrer que la fonction F définie par
F(x) = 2 x – Error! est la primitive sur ]0 ; +  [ de la fonction f définie par f(x) = Error! + Error!
qui vérifie F(1) = 1
2. Déterminer la primitive G de f sur ]0 ; +  [ qui vérifie G(4) = 0
Exercice 3
1. Montrer que la fonction F définie par
F(x) = Error! est la primitive sur ] –  ; +  [ de la fonction
f(x) = – 2
𝑥²+ 𝑥−1
𝑥 4 + 2𝑥²+1
f définie par
qui vérifie F(0) = 1
2. Déterminer la primitive G de f sur ]0 ; +  [ qui vérifie G(1) = 0
6. Primitives des fonctions usuelles.
La fonction …
admet des primitives sur …
et ses primitives ont la
forme …
x 0
x  a ( a  I; R )
I; R
I; R
(n  I; N*)
I; R
x k
(k  I; R)
x  a x + k (k  I; R)
x  Error! xn +1 + k (k 
I; R)
x  xn
x  Error! (n  Error! et n
 1)
]- ; 0[ et ]0 ; +[
x  Error!
]0 ; +[
x  ln(x) + k
(k  I; R)
x  Error!
]0 ; +[
x
(k  I; R)
x  ex
I; R
x  – Error!Error! + k(k
I; R)
x+k
x  ex + k
(k  I; R)
7. Primitives et opérations
a. Primitives de ku (k  I; R* )
Si U est une primitive de la fonction u sur l'ouvert I
3
alors la fonction kU + Cst est une primitive de ku sur I
b. Primitives de u + v
Si U et V sont des primitives de u et v sur I alors U + V + Cst est une primitive de u + v sur I
c. Remarque
il n'y a pas de "formules" concernant les primitives de fonctions de la forme uv et Error!
Exercice 4
Donner la forme générale des primitives des fonctions suivantes :
x Error! x² + x + 1
x Error! x4 – 3x3 + 5 x² + 3x – 2
x Error! 2x6 – Error! x² – Error!
x Error! Error! + x² – 1
x Error! Error! + 2
Exercice 5
Donner la primitive F dont la représentation graphique passe par le point de coordonnées ( 1 ; – 1)
x Error!
x Error!
x Error!
II.
1
– Error!
𝑥4
4
𝑥3
3
2𝑥
+ Error! + 2
–
5
2 𝑒𝑥
3
Intégrale d’une fonction entre « a » et « b »
1. Définition et notation
Si f est une fonction continue sur un intervalle I et si 𝑎 ∈ 𝐼 𝑒𝑡 𝑏 ∈ 𝐼
𝒃
L’intégrale de la fonction f entre a et b , notée ∫𝒂 𝒇(𝒙)𝒅𝒙 , est le nombre F(b) – F(a)
où F est une fonction dérivable sur I telle que F’ = f
𝒃
∫𝒂 𝒇(𝒙)𝒅𝒙 =
On a donc
𝑭(𝒃) − 𝑭(𝒂)
𝒃
∫𝒂 𝒇(𝒙)𝒅𝒙 se lit « intégrale entre a et b de f(x)dx » ou « somme entre a et b de f(x)dx »
Exercice 6
Calculer , si c’est possible , les intégrales suivantes :
1
𝐼1 = ∫0 (𝑥 + 𝑒 𝑥 )𝑑𝑥
1
𝐼2 = ∫−1(𝑥² + 𝑒 𝑥 + 2)𝑑𝑥
2
1
1
𝐼3 = ∫0 (𝑥 2 + 3 𝑒 𝑥 ) 𝑑𝑥
4
1
2
1
𝐼4 = ∫−1 (𝑥 3 + 𝑥 + 𝑒 𝑥 ) 𝑑𝑥
2. Interprétation graphique
Si f est une fonction continue et positive sur l’intervalle
[a ;b] (donc a ≤ 𝒃)
𝒃
∫ 𝒇(𝒙)𝒅𝒙
𝒃
𝒂
alors ∫𝒂 𝒇(𝒙)𝒅𝒙 est l’aire de la partie du plan délimitée par
l’axe des abscisses , la courbe représentative de f et les
droites (verticales) d’équations x= a et x= b
Exercice 7
La fonction f est définie par f(x) = 2 𝑒 𝑥 + 𝑥 3 + x + 1
Justifier que f est positive sur [0 ; 2] puis calculer , en unités
d’aire , l’aire de la partie du plan située sous la courbe (C)
représentative de la fonction f , au dessus de l’axe des abscisses
et entre les droites d’équations x = 0 et x = 2 .
3. Fonction définie par une primitive
Propriété
Si f est une fonction continue sur un intervalle I alors :
La fonction F définie par ∀ x ∈ I
on a donc ∀ x ∈ I
𝒙
F(x) = ∫𝒂 𝒇(𝒕)𝒅𝒕 est la primitive de f sur I qui s’annule en a .
F’(x) = f(x)
Démonstration
𝑥
F(x) = ∫𝑎 𝑓(𝑡)𝑑𝑡 = G(x) – G(a)
On a donc F(x) = G(x) + K avec K = G(a) constante donc F’(x) = G’(x) = f(x) ( car G primitive
de f )
On en déduit que F est aussi une primitive de f sur I
Soit G une primitive de f sur I . On a donc ∀ x ∈ I
𝑎
De plus F(a) = ∫𝑎 𝑓(𝑡)𝑑𝑡 = 0 donc F est bien la primitive de f qui s’annule en a .
Exercice 8
𝑥
Soit F la fonction définie par F(x) = ∫0 (𝑒 𝑡 + 𝑡 ² + 1)𝑑𝑡 .


Etudier les variations de F .
Dresser le tableau de variation de F sur [0 ; 1]
4. Propriétés
a.
Linéarité de l’intégrale
Si f et g sont deux fonctions continues sur l’intervalle I et si a et b sont deux réels de I
Si 𝛼 et 𝛽 sont deux nombres réels
Alors on a les égalités suivantes :
𝒃
𝒃
𝒃
∫𝒂 (𝒇(𝒕) + 𝒈(𝒕))𝒅𝒕 = ∫𝒂 𝒇(𝒕)𝒅𝒕 + ∫𝒂 𝒈(𝒕)𝒅𝒕
5
𝒃
𝒃
∫𝒂 𝜶 × 𝒇(𝒕)𝒅𝒕 = 𝜶 × ∫𝒂 𝒇(𝒕)𝒅𝒕
b.
Une conséquence de la linéarité
Si f est continue sur l’intervalle I et si a et b sont deux réels de I
Alors
𝒂
𝒃
𝒂
∫𝒃 𝒇(𝒙)𝒅𝒙 = – ∫𝒂 𝒇(𝒙)𝒅𝒙 = ∫𝒃 – 𝒇(𝒙)𝒅𝒙
La première égalité découle de la définition par les primitives et la seconde de la linéarité ( avec 𝛼 = –1)
La seconde égalité est intéressante d’un point de vue calcul d’aire
En effet si f est une fonction continue et négative sur [a ; b] ( donc a < 𝑏)
Alors –f est continue et positive sur [a ; b]
𝑏
L’aire « sous la courbe de – f » est donc donnée par A = ∫𝑎 −𝑓(𝑥)𝑑𝑥
𝑏
Aire ∫𝑎 −𝑓(𝑡)𝑑𝑡
𝑏
Donc par A = – ∫𝑎 𝑓(𝑥)𝑑𝑥 .
Pour des raisons évidentes de symétrie par rapport à l’axe des abscisses , l’aire
« sur la courbe de f » ( c’est-à-dire comprise entre la courbe représentative de
f , l’axe des abscisses et les droites d’équations x = a et x = b ) est donc A
𝑏
Aire – ∫𝑎 𝑓(𝑡)𝑑𝑡
Courbe de – f
c.
Relation de Chasles
Courbe de f
Si f est une fonction continue sur l’intervalle I et si a , b et c sont trois réels de I
Alors
𝒃
𝒄
𝒄
∫𝒂 𝒇(𝒕)𝒅𝒕 + ∫𝒃 𝒇(𝒕)𝒅𝒕 = ∫𝒂 𝒇(𝒕)𝒅𝒕
Démonstration facile
𝑐
∫ 𝑓(𝑡)𝑑𝑡
Soit F une primitive de f sur l’intervalle I
𝑏
∫𝑎 𝑓(𝑡)𝑑𝑡
= F(b) – F(a) et
𝑏
𝑐
∫𝑏 𝑓(𝑡)𝑑𝑡
𝑏
= F(c) – F(b)
𝑏
∫ 𝑓(𝑡)𝑑𝑡
𝑐
Donc ∫𝑎 𝑓(𝑡)𝑑𝑡 + ∫𝑏 𝑓(𝑡)𝑑𝑡 = F(b) – F(a) – [ F(c) – F(b)]
𝑐
= F(c) – F(a) = ∫𝑎 𝑓(𝑡)𝑑𝑡
𝑎
(cqfd)
Le graphique ci-contre ,avec f positive et a < 𝑏 < 𝑐 , donne une vision de
la relation de Chasles
d.
Positivité
Si f est une fonction continue sur l’intervalle [a ;b]
et si ,pour tout x de [a ;b] , on a f(x) ≥ 0
alors
𝒃
∫ 𝒇(𝒕)𝒅𝒕 ≥ 𝟎
𝒂
6
Evidence en interprétant l’intégrale comme une aire
Attention ! les bornes doivent être dans l’ordre ( a < b )
e.
Ordre
Si f et g sont deux fonctions continues sur l’intervalle [a ;b]
Et si , pour tout x de [a ;b] on a f(x) ≥ 𝑔(𝑥)
Alors
𝒃
𝒃
∫ 𝒇(𝒕)𝒅𝒕 ≥ ∫ 𝒈(𝒕)𝒅𝒕
𝒂
𝒂
Démonstration simple en utilisant la positivité de l’intégrale et sa linéarité
La fonction h = f – g est continue sur [a ; b] comme somme de fonctions
continues sur [a ; b] et elle est positive sur [a ; b] ( car ∀ x de [a ;b] on a
f(x) ≥ 𝑔(𝑥) donc f(x) – g(x) ≥ 0 )
𝐶𝑔
𝐶𝑓
𝑏
Donc ∫𝑎 ℎ(𝑥)𝑑𝑥 ≥ 0
𝑏
𝑏
𝑏
⇔ ∫𝑎 (𝑓(𝑥) − 𝑔(𝑥))𝑑𝑥 ≥ 0 ⇔ ∫𝑎 𝑓(𝑥)𝑑𝑥 – ∫𝑎 𝑔(𝑥)𝑑𝑥 ≥ 0
𝑏
𝑏
⇔ ∫𝑎 𝑓(𝑥)𝑑𝑥 ≥ ∫𝑎 𝑔(𝑥)𝑑𝑥
(cqfd)
Le graphique ci-contre illustre le résultat dans le cas où les fonctions f et g sont toutes les deux positives .
1. Une conséquence de l’ordre : aire « entre deux courbes »
𝐶𝑔
Si f et g sont deux fonctions continues sur [a ; b]
et si ∀ 𝒙 ∈ [𝒂 ; 𝒃] f(x) ≥ g(x)
alors l’aire A de la partie du plan comprise entre les
courbes représentatives de f et de g et les droites
d’équations x = a et x = b
est donnée , en unités d’aire par :
𝐶𝑓
𝒃
𝑨 = ∫(𝒇(𝒙) − 𝒈(𝒙))𝒅𝒙
𝑏
∫(𝑓(𝑥) − 𝑔(𝑥))𝑑𝑥
𝒂
𝑎
 Remarque :
La positivité des deux fonctions sur [a ; b] n’est pas ici une condition nécessaire
Seul l’ordre des deux fonctions sur [a ; b] est important .
 Démonstration
Partie 1 : Si les deux fonctions sont , en plus , positives sur [a ; b] ,l’aire
qui nous intéresse est la différence entre l’aire sous 𝐶𝑓 et l’aire sous 𝐶𝑔
𝑏
𝐶𝑔
𝑏
Donc elle vaut ∫𝑎 𝑓(𝑥)𝑑𝑥 – ∫𝑎 𝑔(𝑥)𝑑𝑥
donc
𝑏
𝐴 = ∫𝑎 (𝑓(𝑥) − 𝑔(𝑥))𝑑𝑥 u.a.
Partie 2 : Si les deux fonctions ne sont pas positives sur [a ; b]
𝐶𝑓
On peut toujours trouver un réel positif k tel que ∀ 𝑥 ∈ [𝑎 ; 𝑏]
7
On ait f(x) + k ≥ 0 et g(x) + k ≥ 0
En effet g est continue donc bornée sur [a ; b]
Soit k ≥ |𝑚| où m est le minimum de g sur [a ; b] , minimum négatif puisque g prend des valeurs
négatives sur [a ; b] on a donc k ≥ – m et ∀ 𝑥 ∈ [𝑎 ; 𝑏]
g(x) ≥ m
on a ∀ 𝑥 ∈ [𝑎 ; 𝑏]
g(x) + k ≥ m + 𝑘 ≥ 0 ( car k ≥ – m )
Comme f(x) ≥ g(x) on a donc aussi f(x) + 𝑘 ≥ g(x) + k ≥ 0
On peut donc appliquer la partie 1 aux fonctions p = f + k
et q = g + k positives et continues sur [a ; b]
L’aire entre les deux courbes représentatives de p et q est
donc de :
𝑏
𝑏
∫𝑎 (𝑝(𝑥) − 𝑞(𝑥))𝑑𝑥 = ∫𝑎 (𝑓(𝑥) + 𝑘 − (𝑔(𝑥) + 𝑘))𝑑𝑥
𝑏
= ∫𝑎 (𝑓(𝑥) − 𝑔(𝑥))𝑑𝑥 u.a
Il suffit alors de remarquer que les courbes représentatives de p et
q sont les images de celles respectivement de f et g par la
translation de k 𝑗⃗ . L’aire entre les courbes représentatives de f et
g est donc identique à l’aire entre les courbes représentatives de
p et q car la translation conserve les aires .
On en déduit que l’aire cherchée est bien de
𝑏
𝑏
A = ∫𝑎 (𝑓(𝑥) − 𝑔(𝑥))𝑑𝑥 u.a
∫(𝑓(𝑥) − 𝑔(𝑥))𝑑𝑥
𝑎
 Exercice
Soit f la fonction définie par f(x) = 𝑒 −2𝑥+1 – x
Déterminer l’aire entre la représentation graphique de f et la droite d’équation y = x
Exercice
Soient f et g les fonctions définies par f(x) =
1
𝑥−3
et g(x) = −𝑥 + 2
Calculer ,en cm² ,l’aire comprise entre les courbes représentatives de f et g et es droites (verticales)
d’équations x= 4 et x= 6 . le repère est orthogonal de 2 cm d’unité en abscisses et 1cm en ordonnées
III.
Moyenne d’une fonction sur un
intervalle
Point de vue graphique :
Si f est une fonction continue et positive sur [a ;b]
La valeur moyenne de f sur [a ;b] est le nombre m
tel que l’aire du rectangle de longueur (b−𝑎 ) et de
hauteur m soit la même que l’aire « sous la courbe »
8
( grisée sur le dessin )
Point de vue calculatoire
Si f est une fonction continue et positive sur [a ;b]
La valeur moyenne de f sur [a ;b] est le nombre m tel que :
𝟏
𝒃
m=
∫𝒂 𝒇(𝒙)𝒅𝒙
𝒃−𝒂
Exercice 1
Calculer la valeur moyenne de la fonction f définie par f(x) = 𝑒 𝑥+1 + x sur [1 ;3]
Exercice 2
9
1. Donner un encadrement de ∫0 𝑓(𝑥)𝑑𝑥 pour la fonction dessinée ci-dessous
2. En déduire un encadrement de la valeur moyenne sur [0 ;4] de cette fonction
.
9