Listing - WordPress.com

Trigonométrie
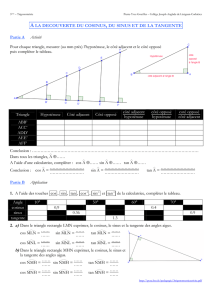
1 Cosinus d’un angle aigu
Définition. Dans un triangle rectangle, le cosinus d’un
angle aigu est égal au quotient du côté adjacent à l’angle
par l’hypoténuse.
adjacent
hypoténuse
cos(
b
C) = CA
CB
Théorème. Si deux triangles rectangles ont des angles
égaux alors les cosinus correspondants sont égaux.
2 Sinus et tangente
Définitions. Dans un triangle rectangle...
le sinus d’un angle aigu
est égal au quotient du
côté opposé à l’angle par
l’hypoténuse.
hypoténuse opposé
sin(
b
C) = AB
CB
la tangente d’un angle
aigu est égal au quotient
du côté opposé à l’angle
par le côté adjacent.
adjacent
opposé
tan(
b
C) = AB
CA
3 Propriétés
Remarque. Le cosinus, le sinus et la tangente d’un angle
aigu s’exprime sans unité.
Théorème. Soit ala mesure d’un angle aigu,
0< cos(a)<1 ; 0 < sin(a)<1
Remarque. Si a > 45° alors tan(a)>1
Formules. Soit ala mesure d’un angle aigu,
[cos(a)]2+[sin(a)]2= 1 ; tan(a) = sin(a)
cos(a)