"f est" choisissons

Fonctions linéaires et affines
I.Fonctions linéaires
A.Définition
•
→
•
•
•!"" #""#" 
"""
 $ % &
 ' ( )&
*→%%#
""
+, −) , %×,)$−) %×−) −%
-#,)$#−)−%
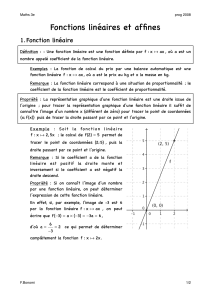
B.Représentation graphique
."!"→%&
+ %&× "
+/0/$ %&×$1
*2"→%&""#""
3$41 2"5%&
×%
5%&
$)
%&
1
1#$
)
+
6%&

•*""/→#
5+""#"7
#""
-"8""#"70#
""/#
5
II.Fonctions affines
A.Définition
9
→9
•""
•""
•!"" #""#" 9
."
 %−)""%4−)
 &""&
/ :""4:
 $−)#"""
B.Représentation graphique
."!"→$9)
+$0"/  )) %
*2"→$9)"""34) 
;)4%
#
5$9)
)
)
%
)
+6$

•*""/→9#
59+"7""/
→"""34 
•#""
• #""##
."!"→$ 
*""/#0 
"7#
-"8"7#""/
#59
III.Détermination d’une fonction affine ou linéaire
A.Fonction linéaire
2#""$ −,
// 
$ −, −,×$
−$
*→−$
B.Fonction affine
2#""% −)−$ $
// 9
% −) −)×%9
−$ −$ $×−$ 9
57
{
−)=%ab
$=−$ab
5$
)
)

{
b=−)−%a
$=−$a−)−%a
…
{
b=,
&
a=−%
&
*
f : x − %
&x, &
IV.Résolution graphique d’un système de deux équations à
deux inconnues
-"/570
{
$xy=&
x−%y='
#
{
y=−$xy
y=x
%−$
4
"#$2)
y=−$x&
2$
y=x
%−$
<%4−) *57"%4
−
)
(le vérifier en résolvant le système précédent par le calcul)
!+/#"""
)
)
<
2$
2)
%
−)
y=$x9&
y=x
%−$