Fonctions usuelles

Fonctions usuelles
Techniques en analyse 3
1
Fonction exponentielle et logarithme népérien.
1.1 Fonction exponentielle.
Théorème 1 (Admis à ce stade.).
Il existe une unique fonction f : R → R, dérivable sur R, telle que
f prend ses valeurs dans R∗+ .
f (0) = 1
Cette fonction
f0 = f
Dénition 2.
La fonction donnée par le théorème ci-dessus est appelée fonction exponentielle et notée
exp :
R → R∗+
.
x 7→ exp(x)
B Attention, science-ction : le nombre exp(x) sera déni en seconde année en donnant un sens à l'écriture
exp(x) =
+∞ k
X
x
k=0
k!
On peut remarquer, au moins formellement, que
=1+x+
d
dx
xk
k!
=
x2 x3
+
+ ···
2!
3!
xk−1
(k−1)! ...
Proposition 3 (Propriété de morphisme de l'exponentielle).
∀x ∈ R ∀x0 ∈ R
exp(x + x0 ) = exp(x) exp(x0 ).
Corollaire 4.
1. ∀x ∈ R
exp(−x) =
2. ∀x ∈ R ∀x0 ∈ R
3. ∀x ∈ R ∀p ∈ Z
1
.
exp(x)
exp(x)
exp(x0 )
exp(px) = exp(x)p .
exp(x − x0 ) =
Notation.
On note e := exp(1), dont la valeur approchée est 2, 7. Notation puissance pour l'exponentielle : exp(x)
0
0
est noté ex . La propriété de morphisme se récrit ∀x, x0 ∈ R ex+x = ex ex .
La première inégalité du lemme ci-dessous va servir dans la preuve de la prochaine proposition. La seconde
prépare la preuve des croissances comparées.
1
PCSI1
L ycée
Albert
S
chweitzer
Lemme 5.
1. Le graphe de l'exponentielle reste au-dessus de sa tangente en 0 :
∀x ∈ R ex ≥ x + 1.
2. Cette dernière inégalité se généralise en
∀n ∈ N ∀x ∈ R+
exp(x) ≥
xn
xn−1
+
+ . . . + x + 1.
n!
(n−1)!
Proposition 6.
La fonction exp réalise une bijection strictement croissante de R dans R∗+ .
Figure 1 Fonction exponentielle.
1.2 Logarithmes.
Dénition 7.
La fonction réciproque de la fonction exponentielle est appelée logarithme népérien et notée ln :
ln :
R∗+ → R
.
x 7→ ln(x)
Elle réalise une bijection de R∗+ dans R.
Remarque. Puisque e0 = 1, on a ln(1) = 0. On retiendra les approximations ln(2) ≈ 0, 69, ln(10) ≈ 2, 3.
2
Figure 2 Fonction logarithme népérien.
Proposition 8.
La fonction ln est dérivable sur R∗+ et
∀y ∈ R∗+
ln0 (y) =
1
.
y
Proposition 9 (Propriété de morphisme du logarithme).
∀y ∈ R∗+ ∀y 0 ∈ R∗+
ln(yy 0 ) = ln(y) + ln(y 0 ).
Corollaire 10.
1. ∀y ∈ R∗+ ln( y1 ) = − ln(y).
2. ∀p ∈ Z ∀y ∈ R∗+ ln(y p ) = p ln(y).
Exemple.
ln(1010 ) = 10 ln(10) ≈ 23.
3
Dénition 11.
Soit a ∈ R∗+ . La fonction logarithme en base a, notée loga , est dénie par
(
loga :
R∗+ → R
x 7→ loga (x) :=
ln(x)
ln(a)
.
La fonction log10 est la plupart du temps notée log.
Exemple. Histoire des grains de riz sur l'échiquier : le roi est sensé donner
64
X
k=1
grains de riz. Soit l'entier N tel que
k−1
2
=
63
X
2k =
k=0
264 − 1
= 264 − 1
2−1
10N ≤ 264 < 10N +1
Appliquons le logarithme en base 10. On obtient
N ≤ log10 (264 ) < N + 1.
ln(2)
On a log10 (264 ) = 64ln(10)
≈ 19.1, ce qui montre que 264 > 1019 = 10 × 109 × 109 .
Dix milliards de milliards de grains de riz, voilà une dette dont le roi ne pourra pas s'acquitter.
1.3 Fonctions hyperboliques.
Dénition 12.
Les fonctions cosinus hyperbolique et sinus hyperbolique sont dénies par

 R → R
ch :
ex + e−x
 x 7→
2

 R → R
sh :
ex − e−x .
 x 7→
2
Proposition 13.
∀x ∈ R ch2 (x) − sh2 (x) = 1.
Remarque. L'ensemble {(x, y) ∈ R2 : x2 − y2 = 1} est une hyperbole.
Proposition 14.
La fonction ch est paire. La fonction sh est impaire. Toutes deux sont dérivables sur R et
∀x ∈ R ch0 (x) = sh(x) et sh0 (x) = ch(x)
4
Figure 3 Fonctions cosinus et sinus hyperboliques.
2
Fonctions puissances.
Soit n un entier naturel non nul et x un nombre réel. Le nombre xn x puissance n est déni par
(facteur x présent n fois).
xn := x × x × . . . × x.
Rappelons notamment que si n1 et n2 sont dans N∗ , on a la relation
xn1 · xn2 = xn1 +n2 .
On dénit couramment x0 = 1, ce qui permet d'étendre la validité de la relation xn+1 = xn · x au cas n = 0.
De plus, on dénit comme suit les puissances négatives : pour n un entier naturel, et x un réel non nul, on
pose
x−n :=
1
x
n
.
On souhaite maintenant donner un sens à l'écriture xa , avec a un réel quelconque, non forcément entier.
Pour cela, remarquons que si p est un entier relatif, et si x ∈ R∗+ ,
p
xp = eln(x) = exp (p ln(x)) ,
(♦)
(∗)
où (∗) utilise le corollaire 4 .3. Ceci motive la dénition suivante.
Dénition 15.
Soit a ∈ R. On appelle fonction puissance d'exposant a la fonction
a
· :
R∗+ → R
.
x 7→ xa := exp(a ln(x))
Exemple. Le nombre
π 3 a toujours
eu
√
un sens pour nous : π × π × π . Le nombre π
Désormais si : il s'agit de exp 2 ln(π) .
√
2
n'en avait pas.
Remarque. Si p ∈ N∗ et x ∈ R∗+ , (♦) montre que la "nouvelle" dénition de xp est cohérente avec l'ancienne.
5
Figure 4 Fonctions puissances d'exposant positif.
Figure 5 Fonctions puissances d'exposant négatif.
On retrouve, pour des exposants réels, les propriétés connues pour des exposants entiers.
Proposition 16.
∀a, b ∈ R ∀x ∈ R∗+
xa+b = xa xb
x−a =
1
xa
(xy)a = xa y a
(xa )b = xab .
La proposition suivante étend pour une puissance quelconque des propriétés d'abord montrées pour les
puissances entières.
Proposition 17.
∀a ∈ R, ∀x ∈ R, ∀y ∈ R∗+
(ex )a = eax
6
et
ln (y a ) = a ln(y).
Proposition 18.
Soit a ∈ R. La fonction x 7→ xa est dérivable sur R∗+ , de dérivée x 7→ axa−1 . De plus,
1. si a ∈ R∗+ la fonction x 7→ xa est croissante sur R∗+ , et lim xa = 0.
x→0+
2. si a ∈
R∗−
la fonction x 7→
3. la fonction x 7→
x0
xa
est décroissante sur
est constante sur
R∗+
et lim
x→0+
R∗+
x0
et lim xa = +∞.
x→0+
= 1.
Corollaire 19.
Soit a ∈ R∗ . La fonction puissance x 7→ xa réalise une bijection de R∗+ dans lui-même, et sa
1
fonction réciproque est la fonction puissance x 7→ x a .
Notation. Pour tout
radical : pour x ∈
n ∈ N∗ , la puissance 1/n, réciproque de la puissance n, est notée avec un symbole
√
√
on note x1/n = n x, avec notamment x1/2 = x.
R∗ +,
Comparons les fonctions puissances aux fonctions exponentielles et logarithme.
Proposition 20 (Croissances comparées).
Soit a ∈ R∗+ . On a les limites suivantes.
xa
= 0;
x→+∞ ex
lim
lim |x|a ex = 0;
x→−∞
lim
x→+∞
ln(x)
= 0;
xa
lim xa ln(x) = 0.
x→0+
Corollaire 21.
Soit a ∈ R∗+ , p > 1 et q ∈] −1, 1[. On a les limites suivantes.
na
= 0,
n→+∞ pn
lim
3
et
lim na q n = 0.
n→+∞
Fonctions circulaires.
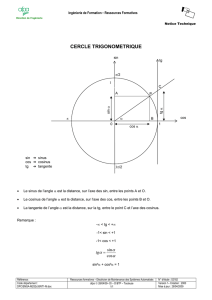
3.1 Dénition géométrique du cosinus et du sinus d'un réel, rappels.
On considère, dans un repère orthonormé du plan, le cercle unité et les points O(0, 0), I(1, 0), et J(0, 1).
Notons D la droite parallèle à (OJ) passant par I . L'ensemble des réels lui est identié : à tout réel x, on
associe le point (1, x) sur D. Notamment, le réel 0 est identié à I ∈ D. On va maintenant agrafer la droite
D au cercle en I et enrouler D sur le cercle : les réels positifs vont l'être dans le sens direct (antihoraire),
et les réels négatifs dans le sens indirect. Pour x réel, on notera M (x) le point du cercle sur lequel a été
enroulé le point (1, x) (voir gure). Attention : le cercle est de longueur 2π et la droite est innie : il va falloir
faire plusieurs tours...
7
Figure 6 Enroulement de la droite réelle sur le cercle trigonométrique.
Plus formellement : si x ∈ [0, 2π], le point M (x) associé est tel que la longueur de l'arc de cercle allant de
I à M (x) dans le sens direct est x. Si on a x ∈ [2kπ, 2(k + 1)π], pour k ∈ N, alors le point M (x) associé sur
le cercle est tel que la longueur de l'arc entre I et M (x) est x − 2kπ (on a fait k fois le tour du cercle). La
longueur x de l'arc
cercle IM (x) (éventuellement avec plusieurs tours de cercle), est une façon de mesurer
−→de−−
−−→
l'angle orienté OI, OM (x) . Si x ∈ [0, 2π], 180x/π est une mesure en degrés de ce même angle orienté.
Dénition 22.
Soit x ∈ R et M (x) le point correspondant sur le cercle trigonométrique, obtenu par enroulement.
On appelle cosinus de x son abscisse et sinus de x son ordonnée, que l'on note respectivement
cos(x) et sin(x). Ceci dénit les fonctions
cos :
R → [−1, 1]
x 7→ cos x
et
sin :
R → [−1, 1]
.
x 7→ sin x
Un peu de géométrie du triangle amène les valeurs notables suivantes :
x 0 π2 π 3π
2π
2
cos x 1 0 −1 0 1
sin x 0 1 0 −1 0
8
π
√6
3
2
1
2
π
√4
2
√2
2
2
π
3
1 .
√2
3
2
3.2 Formulaire de trigonométrie.
L'utilisation des symétries sur le cercle trigonométrique amène les formules ci-dessous.
Proposition 23.
Pour tout réel x ∈ R,
cos(−x) = cos x
sin(−x) = − sin x
cos( π2 − x) = sin x
sin( π2 − x) = cos x
cos(π − x) = − cos x
sin(π − x) = sin x
cos(x + 2π) = cos x
sin(x + 2π) = sin x.
Corollaire 24.
La fonction cos est paire, et la fonction sin impaire. Elles sont toutes deux 2π -périodiques. Le
→
−
graphe de sin se déduit de celui de cos par la translation de vecteur π2 i .
Le théorème de Pythagore appliqué OHM (x) permet d'établir la relation suivante.
Proposition 25.
∀x ∈ R
cos2 x + sin2 x = 1.
Proposition 26 (Formules d'addition).
Pour tous réels a, b ∈ R,
cos(a − b) = cos a cos b + sin a sin b
cos(a + b) = cos a cos b − sin a sin b
sin(a − b) = sin a cos b − sin b cos a
sin(a + b) = sin a cos b + sin b cos a
Corollaire 27 (Formules de duplication).
Pour tout a ∈ R,
cos 2a = cos2 a − sin2 a = 2 cos2 a − 1 = 1 − 2 sin2 a
9
sin 2a = 2 cos a sin a.
Figure 7 Fonction cosinus.
Figure 8 Fonction sinus.
3.3 Dérivation du cosinus et du sinus (HP).
Lemme 28.
i πi
∀x ∈ 0,
2
Preuve.
cos x ≤
sin(x)
≤ 1.
x
Soit x ∈ 0, π2 . On note M = M (x) le point obtenu sur le cercle trigonométrique par enroulement de la
droite. Notons C(x) la portion de disque délimitée par O, I et M (pleine sur la gure suivante). On lit sur
la gure l'inégalité
Aire(OIM ) ≤ Aire (C(x)) ≤ Aire(OIT ).
(1)
10
Figure 9 Encadrement de
sin(x)
x .
• On sait que C( π2 ) est d'aire π4 . Une règle de trois nous apprend que C(x) est d'aire x2 .
• Le triangle OIM est de base OI = 1 et de hauteur HM = sin(x). On a donc Aire(OIM ) = 1×sin(x)
.
2
IT
OI
×OI
sin x
tan x
• Le théorème de Thalès donne HM
= OH
d'où IT = HMOH
= cos
=
tan
x
.
On
a
donc
Aire(OIT
)
=
x
2 .
Les inégalités (1) donnent donc
x
sin x
sin x
≤ ≤
.
2
2
cos x
ce qui entraîne bien
cos(x) ≤
sin(x)
≤ 1.
x
Proposition 29.
Les fonctions cosinus et sinus sont dérivables sur R, de dérivées
cos0 = − sin
et
sin0 = cos .
Preuve.
• Soit x ∈ R. On va dériver la fonction sin en x c'est à dire s'intéresser au taux d'accroissement
sin(x + h) − sin x
.
h
Il nous faut montrer que ce dernier a une limite lorsque h tend vers 0, et que cette limite est cos x.
L'utilisation des formules d'addition amène, pour tout h 6= 0,
11
sin x cos h + cos x sin h − sin x
sin h
cos h − 1
sin(x + h) − sin x
=
= cos x
+ sin x
.
h
h
h
h
Ainsi, la proposition est démontrée si on prouve
1 − cos h
−→ 0.
h→0
h
sin h
−→ 1 et
h h→0
La première limite découle du Lemme 28, grâce au théorème des gendarmes. Pour la seconde, on calcule
(1 + cos h) (1 − cos h)
1 − cos2 h
sin2 (h)
sin h
=
=
= sin h ×
,
h
h
h
h
d'où
1 − cos h
sin h
sin h
0
=
×
−→
× 1 = 0.
h
1 + cos h
h h→0 2
x
−→ cos(x) × 1 + 0 = cos(x). Ceci achève de démontrer que sin est dérivable
On a donc bien sin(x+h)−sin
h
h→0
en x, de dérivée cos x.
• Rappelons que pour tout x ∈ R,
cos(x) = sin
π
2
−x .
Ainsi, cos est dérivable sur R comme composée de fonctions dérivables sur R et
∀x ∈ R
cos0 (x) = (−1) sin0
π
π
− x = − cos
− x = − sin(x).
2
2
3.4 Fonction tangente.
Dénition 30.
On appelle fonction tangente et on note tan la fonction dénie par
(
tan :
R\
π
2
+ kπ, k ∈ Z → R
7→ tan(x) :=
x
Notation. Dans la suite, on peut noter Dtan = R \
π
2
sin x .
cos x
+ kπ, k ∈ Z .
Proposition 31.
Sur Dtan , la fonction tangente est impaire et π -périodique.
Remarque. On en déduit qu'il sut d'étudier la fonction tangente sur ] − π2 , π2 [.
12
Figure 10 Fonctions tangente.
Proposition 32.
lim tan(x) = +∞
x→ π2
x< π2
et
lim tan(x) = −∞
x→− π2
x>− π2
Proposition 33.
La fonction tangente est dérivable sur Dtan et
∀x ∈ Dtan
tan0 (x) =
1
= 1 + tan2 (x).
cos2 (x)
Remarque. On en déduit notamment que la fonction tangente est strictement croissante sur
] − π2 , π2 [ et
que sa tangente à l'origine est la droite d'équation y = x (on peut montrer que le graphe est au-dessus de
cette tangente à droite de l'origine).
13
4
Fonctions circulaires réciproques.
Le théorème de la bijection monotone permet de montrer que
• la fonction sin réalise une bijection croissante de [− π2 , π2 ] dans [−1, 1].
• la fonction cos réalise une bijection croissante de [0, π] dans [−1, 1].
• la fonction tan réalise une bijection croissante de ] − π2 , π2 [ dans R.
Ceci permet de se donner les dénitions suivantes.
Dénition 34.
• On appelle fonction
arcsinus et on note
π π
arcsin : [−1, 1] → [− , ]
2 2
la réciproque de sin : [− π2 , π2 ] → [−1, 1].
• On appelle fonction
arccosinus et on note
arccos : [−1, 1] → [0, π]
la réciproque de cos : [0, π] → [−1, 1].
• On appelle fonction
arctangente et on note
arctan : R →] −
π π
, [
2 2
la réciproque de la fonction tan :] − π2 , π2 [→ R
Figure 11 Fonction arcsinus.
Figure 12 Fonction arccosinus.
14
Figure 13 Fonctions arctangente.
Proposition 35.
∀x ∈ [−1, 1]
∀x ∈ [−1, 1]
∀x ∈ R
Exemple.
∀x ∈ [− π2 , π2 ]
∀x ∈ [0, π]
∀x ∈] − π2 , π2 [
sin(arcsin(x)) = x
cos(arccos(x)) = x
tan(arctan(x)) = x
arcsin(sin(x)) = x
arccos(cos(x)) = x
arctan(tan(x)) = x
π
arccos cos( 5π
)
= 3.
3
Proposition 36.
Les fonctions arcsin et arccos sont dérivables sur ] − 1, 1[ et
∀x ∈] − 1, 1[
arcsin0 (x) = √
1
1 − x2
et
arccos0 (x) = − √
La fonction arctan est dérivable sur R, et
∀x ∈ R
arctan0 (x) =
1
.
1 + x2
Proposition 37.
∀x ∈ [−1, 1]
arccos(x) + arcsin(x) =
15
π
.
2
1
.
1 − x2