sin arc

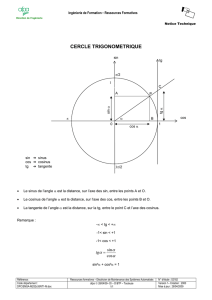
STIA 3
HARMONISATION
MATHEMATIQUES
Support de cours
1
CHAPITRE 1
GENERALITES SUR LES FONCTIONS
I. Rappels
I.1. Définitions
Définition 1
Soit I un sous ensemble de  (intervalle de  ou réunion d’intervalles de ), définir
une fonction f de I dans , c’est associer à chaque réel x de I, un unique réel noté
f (x) .
I est l’ensemble de définition de f ; f est définie sur I.
Cette définition peut être schématisée comme suit :
I

f :
x
f (x)
Définition 2 (Courbe représentative)
Soit f une fonction définie sur un ensemble I :
La courbe représentative de f dans un repère orthogonal (o; i , j ) est l’ensemble des
points M de coordonnées ( x ; f (x) ), avec x élément de I. Ainsi, dire que M (x , y)
appartient à cette courbe équivaut à dire que x  I et y = f (x) .
y
f(x1)
j
x1
O i

2


x
I.2. Sens de variation
Théorème 1
f est une fonction définie sur un intervalle I de .
On dit que f est croissante sur I si quels que soient les réels u et v de I,
u <v
implique
f(u) ≤
f(v)
On dit que f est décroissante sur I si quels que soient les réels u et v de I,
u <v
implique
f(u) ≥
f(v)
On dit que f est monotone sur I si elle est croissante ou décroissante sur I.
On dit que f est strictement croissante sur I si quels que soient les réels u et v de I,
u <v
implique
f(u) <
f(v)
On dit que f est strictement décroissante sur I si quels que soient les réels u et v de I,
u <v
implique
f(u) >
f(v)
On dit que f est strictement monotone sur I si elle est strictement croissante ou
strictement décroissante sur I.
I.3. Fonctions paires/impaires
Définition 3
Une fonction f définie sur I est paire si quel que soit x dans I, alors – x est aussi dans
I et f(-x) = f(x).
La courbe représentant f dans un repère orthogonal est symétrique par rapport à
l’axe des ordonnées.
Définition 4
Une fonction f définie sur I est impaire si quel que soit x dans I, alors – x est aussi
dans I et f(-x)=-f(x).
La courbe représentant f dans un repère orthogonal est symétrique par rapport à
l’origine du repère.
II. Les fonctions de référence
Dans ce premier chapitre, cinq fonctions de référence sont définies. Les fonctions
trigonométriques sont présentées dans le chapitre 2 "Rappels de trigonométrie". Les
fonctions exponentielle et logarithme sont étudiées en détails aux chapitres 5 et 6.
II.1. Fonction affine
Définition5
Une fonction affine est une fonction f : x
deux réels fixés.
Sens de variation :
Si a 
> 0, f est strictement croissante sur .
Si a < 0, f est strictement décroissante sur .
Si a = 0, f est constante sur .

3


a x + b définie sur  où a et b sont
II.2. Fonction inverse
Définition 6
La fonction inverse est la fonction f : x
1
x
définie sur    ; 0    0 ;   .
Sens de variation :
f est strictement décroissante sur   ; 0  et sur  0 ;   .
Son tableau de variation est :
x
-∞
0
+∞
1
x
II.3. Fonction valeur absolue
Définition 7
La fonction valeur absolue est la fonction f : x
x définie sur .
Si x ≥ 0 alors x = x et si x ≤ 0 alors x = -x.
Sens de variation :
f est strictement croissante sur  0 ;   et strictement décroissante sur   ; 0  .
Son tableau de variation est :

x

-∞
0
+∞
x
0
II.4. Fonction « racine carrée »
Définition 8
La fonction « racine carrée » est la fonction f : x
x définie sur  0 ;   .
Sens de variation :
f est strictement croissante sur  0 ;   .
Son tableau de variation est :
x
0
+∞
x

4
II.5. Fonctions polynômes
Définition 9
La fonction f définie sur  par f (x) = a x n est appelée fonction monôme de coefficient
a. Lorsque a est non nul, n est le degré de cette fonction monôme.
Une fonction polynôme est une somme de fonction monômes


f :
a
x
i
xi
i
III. Opérations sur les fonctions
III.1. Opérations algébriques
Définition 10
Dire que deux fonctions f et g sont égales signifie qu’elles ont le même ensemble de
définition, I, et que pour tout x de I, f (x) = g (x) .
Définition 11
f et g sont deux fonctions définies respectivement sur If et Ig et x appartenant à If et
Ig, le tableau ci-dessous donne les définitions des opérations algébriques sur les
fonctions.
Opération
Notation
Définition
Somme
f + g
x
f(x)  g(x)
Différence
f - g
x
f(x) - g(x)
Produit
f. g
x
f(x) g(x)
Quotient
f
g
x
f (x)
g (x)
Définie pour
x  If Ig
x  I f Ig et g(x)0
III.2. Composition de fonction
Théorème 2
Soient f et g deux fonctions définies respectivement sur If et Ig.
La fonction g f est la fonction définie par ( g f )(x)=g(f(x)).
Cette fonction est définie sur l’ensemble des réels x appartenant à If tels que f (x)
appartient à Ig.

5
CHAPITRE 2
RAPPELS DE TRIGONOMETRIE
I- Les fonctions trigonométriques
I.1. La fonction cosinus
Soit x un nombre réel et M le point du cercle
trigonométrique associé à x . On appelle
cosinus de x l'abscisse du point M dans le
repère orthonormé O ; i ; j .


La fonction cosinus est la fonction f : x
cos x définie sur IR.
La fonction cosinus est une fonction paire, périodique de période 2π et bornée ( x 
IR, - 1  cos x  1 ).
Son tableau de variation sur 0 ;   :
I. 2. La fonction sinus
Soit x un nombre réel et M le point du cercle
trigonométrique associé à x . On appelle sinus
de x l'ordonnée du point M dans le repère
orthonormé O ; i ; j .


La fonction sinusest la fonction f : x
sin x définie sur IR.

6
La fonction sinus est impaire, périodique de période 2π et bornée ( x  IR,
- 1  sin x  1 ).
Son tableau de variation sur 0 ;   :
I.3. La fonction tangente
sin x .
Si cos x est non nul, on appelle tangente de x le réel noté tan x défini par : tan x = cos
x
La fonction tangente est impaire et périodique de période π.
est défini
géométriquement comme

indiqué sur
la figure ci-contre.
tan x
La cotangente (notée cotan) d'un réel est égale au quotient de son cosinus par son sinus.
x.
Pour x  0 modulo , cotan x = cos
sin x
I.4. Les fonctions trigonométriques réciproques
I.4.1. Fonction Arc-sinus
On appelle Arc-sinus (et on note arcsin) la fonction réciproque de sin.
 x  [-/2 ; /2], y  [-1 ; 1], y = sin x  x = arcsin y.


sin (Arcsin x) = x
Arcsin(sin x) = x si x  [-/2 ; /2]
I.4.2. Fonction Arc-cosinus
On appelle Arc-cosinus (et on note arccos) la fonction réciproque de cos.
 x  [0, ], y  [-1 ; 1], y = cos x  x = Arccos y.
Arccos (-1) = 
Arccos (1) = 0
cos(Arccos x)=x pour x  [-1 ; 1] Arccos(cos x)=x pour x  [0 ; ]
7
I.4.3. Fonction Arc-tangente
On appelle arc-tangente (et on note arctan) la fonction réciproque de la fonction
tangente.
 x  ] -/2 ; /2[ et y  R, y = tan x  x = arctan(y)
Pour x  R, tan(Arctanx) = x
Pour x  ]-/2 ; /2[, Arctan(tan x) = x
II. Cercle trigonométrique - angles associés et remarquables
 x
cos ( x)   cosx
sin ( x)  sin x
cos ( x)   cos x
cos (2 x)  sin x
2
 x
x
 x
-x
sin ( x)   sin x
sin (2 x)  cos x
cos (x)  cos x
sin (x)   sin x
Angles remarquables
 (rad)
0

6

4

3

2
Sin 
0
1
2
2
2
3
2
1
Cos 
1
Tan 
0
3
2
2
2
1
2
3
3
0
∞
1
3
III. Formulaire
III.1. Formules d'addition
cos (a-b) = cos a cos b + sin a sin b
cos (a+b) = cos a cos b - sin a sin b
sin (a-b) = sin a cos b - cos a sin b
sin (a+b) = sin a cos b + cos a sin b
8
a  tan b
tan (ab)  1 tan
 tan a . tan b
a  tan b
tan (ab)  1 tan
 tan a . tan b
III.2. Formules de duplication
cos (2a)  cos 2 a  sin 2 a  2 cos 2 a  1  1  2 sin 2 a cos (3a)  4 cos3 a  3 cosa
sin (2a)  2 sin a cos a
sin (3a)  3 sin a  4 sin 3 a
tan (2a)  2 tan 2a
1  tan a
3 tan a  tan 3 a
tan (3a) 
1  3 tan 2 a
III.3. Formules de linéarisation
(2a)
cos 2 a  1  cos
2
(2a)
sin 2 a  1  cos
2
1  cos (2a)
tan2 a  1  cos (2a)
cos 3 a  cos (3a) 4 3 cos a sin 3 a  sin (3a)4 3 sin a tan3 a  sin (3a)  3 sin a
cos (3a)  3 cos a
cos a . cos b 1
2 cos (ab)  cos (ab)
cos a . sin b  1
2 sin (ab)  sin (ab)
sin a . sin b  1
2 cos (ab)  cos (ab)
III.4. Relations entre cos, sin et tan
cos 2 x  sin 2 x  1
1  tan2 x 
1
cos2 x
III.5. Transformations
a-b
sin a + sin b = 2 sin a+b
2 . cos 2
a+b
sin a -sin b = 2 sin a-b
2 . cos 2
a-b
cos a + cos b = 2 cos a+b
2 . cos 2
a-b
cos a - cos b = - 2 sin a+b
2 . sin 2
9


CHAPITRE 3
LIMITES ET CONTINUITE
I. Limite d’une fonction en   et  
Définition 1
Soit f une fonction définie sur un intervalle de type  x 0 ;  . On dit que f tend vers
+ ∞ quand x tend vers + ∞ si, pour tout nombre A, l’intervalle  A ;   contient
toutes les valeurs prises par la fonction pour x assez grand.
f(x)   ou lim
f   .
On écrit lim
+
x
Fonctions de références
a> 0
lim
a x + b = + ,
+
lim
x = + ,
+
a< 0
1 = 0+
lim
+ x
lima x ++b = - 
Définition 2
f (x)    si lim
On dit que f vérifie lim
 f (x)   .
x
x
Définition 3
Soit f une fonction définie sur un intervalle du type  x 0 ;  . On dit que f tend vers
 quand x tend vers +∞ si tout intervalle ouvert contenant  contient toutes les
f (x)   ou lim
f  .
valeurs de la fonction pour x assez grand. On écrit lim

x
On dit que la courbe C représentative de la fonction f admet en + ∞ une asymptote
horizontale ∆ d’équation y = .
Définition 4
Soit f une
 fonction définie sur un intervalle du type  x 0 ;  . Si f (x) peut s’écrire
 (x)  0 , on dit que la courbe C
sous
 la forme a x + b +  (x) avec a ≠ 0 et lim
x
représentative de f admet en +∞ une asymptote oblique ∆ d’équation y = a x + b .
II. Limite d’une fonction en un réel x0
Définition 5
Soit f une fonction définie au voisinage de x0 (et pas nécessairement en x0). On dit
que f tend vers + ∞ quand x tend vers x0 si tout intervalle  A ;   contient toutes
les valeurs de la fonction pour x assez proche de x0.

10
On écrit limf(x)   ou limf    .
xx0
x0
On dit alors que la courbe C représentative de la fonction f admet une asymptote
verticale ∆ d’équation x = x0.
Définition 6
Soit f une fonction définie sur un intervalle ouvert contenant x0.
On dit que f tend vers  quand x tend vers x0, si tout intervalle ouvert contenant 
contient toutes les valeurs de la fonction pour x assez proche de x0.
On écrit limf (x)   ou limf   .
xx0
x0
III. Limites et comparaison des fonctions
Propriété 1 (Théorème des gendarmes pour les fonctions)
Soient f , g et h trois fonctions vérifiant, au voisinage de x0 (x0 étant éventuellement
égale à + ∞ ou à- ∞), f (x)  g (x)  h (x) .
Si f et h admettent la même limite  quand x tend vers x0, alors g admet aussi une
limite en x0 et lim g (x)   .
xx0
Propriété 2
Soit f et g deux fonctions vérifiant, sur un intervalle  A ;  , f (x)  g (x) .
f(x)    , alors lim
g(x)    .
Si lim
x
x

g(x)    , alors lim
f (x)   .
Si lim
x
x
IV. Limites et opérations sur les fonctions
IV.1. Limite d’une somme
Si limf  …
et si limg  …
c
c
c
+∞
-∞
+∞
c’
+∞
-∞
+∞
-∞
-∞
x0
x0



11
alors lim (f g) 
x0
IV.2. Limite d’un produit
Si limf  …
x0
c
c>0
c<0
+∞
0
-∞
et si limg  …
x0
alors lim (f  g) 
x0
c’
+∞
+∞
-∞
-∞ ou +∞
-∞
IV.3. Limite de l’inverse
Si limf  …
alors lim (1 ) 
x0
x0
f
c≠0
+∞
-∞
0, avec f>0
0, avec f<0
0
IV.4. Limite d’une composition de fonction
f  b et si lim
g  c , alors lim
(g f)  c .
Si lim
a
b
a
V. Limite et formes indéterminées

Les quatre types essentiels de formes indéterminées sont :
 la somme de deux fonctions qui admettent pour limite l’une + ∞, l’autre - ∞,
 le produit d’une fonction qui admet une limite infinie et d’une fonction qui
admet une limite nulle,
 le quotient de deux fonctions qui admettent chacune une limite nulle,
 le quotient de deux fonctions qui admettent chacune une limite infinie.
Méthodes pour lever les indéterminations
Méthode 1 : factoriser le terme prépondérant (F.I. du type (+ ∞) + (- ∞) ou ∞/∞)

- Repérer le terme prépondérant
- Factoriser ce terme
- Étudier les limites de chaque facteur
- Conclure
Méthode 2 : utiliser la quantité conjuguée (F.I. pour des expressions contenant des √
ou lorsque la méthode 1 est inefficace)
- Multiplier et diviser l'expression par sa quantité conjuguée
- Simplifier
- Étudier les limites du numérateur et du dénominateur
- Conclure
12
VI. Fonctions continues
VI.1. Définitions
Définition 7
Soit f une fonction définie sur un intervalle I et a un élément de I. On dit que f est
f (x)  f (a) .
continue en a si lim
xa
Définition 8
Soit f une fonction définie sur un intervalle I. On dit que f est continue sur I si elle
est continue en tout point de I.
Propriété 3
Les fonctions polynômes, trigonométriques et racine carrée ainsi que toute fonction
construite à partir de ces fonctions par addition, multiplication, division ou
composition, sont continues sur tout intervalle où elles sont définies.
VI.2. Théorème des valeurs intermédiaires
Théorème
Soit f une fonction définie et continue sur un intervalle I et, a et b deux nombres de
I. Pour tout nombre k compris entre f (a) et f (b) , il existe un nombre c compris entre
a et b tel que f (c) = k .
Propriété 4

Si f est une fonction
continue et strictement monotone sur l’intervalle a ; b, alors,
pour tout nombre k compris entre f (a) et f (b) , l’équation f (x) = k a une solution c
unique dans l’intervalle a ; b.

Propriété 5
Si f est une fonction continue et strictement monotone sur l’intervalle a ; b ( b étant
f (x) ,
un nombre ou + ∞), alors, pour tout nombre k compris entre f (a) et lim
xb
l’équation f (x)  k a une solution c unique dans l’intervalle a ; b.
13




CHAPITRE 4
DERIVEES ET PRIMITIVES
I. Nombre dérivé et interprétations
Propriété 1
Soit f la fonction définie sur un intervalle I et x0 un élément de I. Les deux
propositions suivantes sont équivalentes :
 Le taux de variation de f entre x0 et x0+ h admet une limite finie l quand h
tend vers 0 :
lim
h0
f (x0 h)  f (x0)
l
h
 Pour tout h tel que x0+ h soit dans I, on peut écrire :
 (h)  0.
f (x0 + h) = f (x0) + l h + h  (h) avec lim
h 0
L'équation y = f (x0) + (x - x0) . f ' (x0) est l'équation de la tangente (T) à la courbe
représentative de la fonction f au point x0.
Définition 1
Lorsque l’une des propositions de la propriété 1 est vraie, on dit que f est dérivable
en x0. Le nombre l s’appelle nombre dérivé de f en x0. On le note f ' (x0) .
II. Fonction dérivée, dérivées successives
Définition 2
Soit f une fonction dérivable en tout x d’un intervalle I.
On dit que f est dérivable sur I. On appelle fonction dérivée de f , notée f ' , la
f'(x) qui, à tout nombre x de I, associe le nombre dérivé de f en x .
fonction x


Propriété 2
Si une fonction f est dérivable sur un intervalle I, alors f est continue sur I.
Définition 3
Soit f une fonction dont la dérivée f ' est dérivable.
On appelle dérivée seconde de f , la fonction dérivée de la fonction f ' . On la note
f ' ou f (2).
On définit de même la dérivée n-ième de f, notée f (n).
14

Fonctions dérivées des fonctions usuelles
Fonction
x
Fonction dérivée
Validité de la formule
k (k : constante)
x
x
x
xn (nZ*)
x
1
x
x
x
x
sin x
x
cos x
x
tan x
x
cotan x
x
arcsin x
x
arccos x
x
arctan x
Fonctions dérivées et opérations
Soit u et v, deux fonctions continues et dérivables :
Fonction
Fonction dérivée
Remarque
u+v
k.u (k : constante)
u.v
u
v
un (nZ*)
u
Propriété 3 : fonction dérivée d’une fonction composée
Si g est une fonction dérivable en x0 et f une fonction dérivable en g (x0) , alors
f g est dérivable en x0 et on a (f g) ' (x0)  f' g (x0) g' (x0) .
15


III. Applications de la fonction dérivée
Propriété 4
Soit f une fonction dérivable sur un intervalle I.
 f est constante sur I si, et seulement si, la dérivée f ' est nulle sur I.
 f est strictement croissante sur I si, et seulement si, la dérivée f ' est strictement
positive sur I (éventuellement nulle en des points isolés).
 f est strictement décroissante sur I si, et seulement si, la dérivée f ' est strictement
négative sur I (éventuellement nulle en des points isolés).
Conséquence
Si f est une fonction dérivable sur un intervalle I dont la dérivée f ' est strictement
positive (négative) sur I, éventuellement nulle en des points isolés, alors f est
continue strictement croissante (décroissante).
Propriété 5
Soit f une fonction dérivable sur un intervalle a ; b noté I et x0 appartenant à I. Si la
dérivée f ' s’annule et change de signe en x0, alors f admet un extremum local en x0.
IV. Primitives d’une fonction
Définition 4
Soit f une fonction définie sur un intervalle I.
On appelle primitive de f sur I une fonction F, dérivable sur I, telle que, pour tout x
appartenant à I, F’(x) = f(x).
Théorème

Toute fonction continue sur un intervalle I admet des primitives sur I.

Propriété 6
Soit F une primitive de f sur un intervalle I.
 Pour tout nombre k, x
F(x) + k est aussi une primitive de f sur I.
 Si G est une autre primitive de f sur I, alors il existe un nombre k tel que, pour

tout x de I, G(x) = F (x) + k.

Propriété 7
Soit f une fonction admettant des primitives sur un intervalle I.
Un réel x0 de I et un réel y0 étant donnés (appelés « conditions initiales »), il existe
une unique primitive F de f sur I telle que F (x0) = y0.
16
CHAPITRE 5
FONCTION EXPONENTIELLE
I. La fonction exponentielle
Définition 1
Soit a un nombre réel. On appelle solution sur l’intervalle I de l’équation
différentielle Y ' = a Y toute fonction, dérivable sur I, qui vérifie sur I : f ' = a f .
Propriété 1 (Théorème d’existence)
Il existe une fonction f , dérivable sur IR, solution de l’équation différentielle Y' = Y et
telle que f (0) = 1. Cette fonction est appelée fonction exponentielle. On note cette
fonction x exp (x) ou x ex pour tout élément x de IR.
Le nombre réel e = exp (1)  2,72
Propriété 2
La fonction exponentielle est strictement positive sur IR.
Propriété 3
Soit a un réel donné. Les solutions de l’équation différentielle Y ' = a Y sont les
fonctions définies sur IR par f(x) = k exp (ax) où k est une constante réelle.
Propriété 4
Pour tous nombres réels a et b, exp (a + b) = exp (a)  exp (b) .
Conséquences
Pour tous nombres réels a et b :
e a+ b = e a e b,
e -a = 1a ,
e
e a-b =
ea
eb
Pourtout nombre réel a et tout nombre rationnel r : e ra = (e a) r .

II. Étude de la fonction x

ex
17
La fonction x e x est solution de l’équation différentielle Y ' = a Y et f(o) = 1 ; elle est
dérivable sur IR donc continue sur IR, et égale à sa dérivée. De plus, x e x est
strictement croissante sur IR.
Propriété 4 (limites)
lim
x0
ex - 1
=1
x
lim
ex = +
x
lim
ex = 0
x
Tableau de variation de la fonction exponentielle
x
-∞
0
1
+∞
+∞
ex
e
1
0

Conséquences
x
Pour tout
 nombre réel x : e > 0 .
Pour tous nombres réels x et y : ex = ey équivaut à
ex > ey équivaut à
Propriété 5

Soit u une fonction définie sur un intervalle I.
Si u est dérivable sur I, alors la fonction x e
x u'(x)  e u(x) .
Propriété 6
lim
x
ex
= +
x
lim
x ex = 0
x
Conséquences
Pour tout n, nombre entier strictement positif :
lim
x
ex
= +
xn
lim
xn ex = 0
x
18
u(x)
x=y
x > y.
est dérivable sur I et sa dérivée est
CHAPITRE 6
FONCTIONS LOGARITHMES
I. Logarithme népérien d’un nombre
Propriété 1
Pour tout nombre réel a strictement positif, il existe un réel unique  tel que e   a .
On appelle ce nombre le logarithme népérien de a. On le note ln (a) ou ln a .
Conséquences
 ln 1 = 0 et ln e = 1.
 Pour tout nombre réel a strictement positif, e ln a = a .
 Pour tout nombre réel a, ln (ea) = a .
Propriété 2
Pour tous nombres réels a et b strictement positifs : ln a b = ln a + ln b .
Conséquences
 Pour tous nombres réels a et b de l’intervalle  0 ; +   : ln ab = ln a - ln b .
 Pour tout nombre réel a de l’intervalle  0 ; +   :
ln 1 = - ln a et ln a = 1 ln a .
a
2
 Pour tout nombre réel a de l’intervalle  0 ; +   et tout nombre rationnel r :
ln a r = r ln a .
II. Fonction logarithme népérien

Définition 1
On appelle fonction logarithme népérien la fonction, notée ln, qui à tout x de
l’intervalle  0 ; +   associe ln x.

Propriété 3
La fonction ln est dérivable sur l’intervalle  0 ; +   .

La fonction ln est la primitive de la fonction x

s’annule en 1.

19
1 sur l’intervalle
x
 0 ; +   qui
Propriété 4
ln (x+1) = 1
lim
x0
x
lim
ln
x
=-
x0
ln x = 1
lim
x1 x-1
lim
ln x = + 
x
Tableau de variations de la fonction logarithme népérien
x
0
1
e
+∞
+∞
ln x
1
0
-∞
Conséquences
 ln x négatif sur l’intervalle  0 ; 1  et positif sur l’intervalle  1 ; +   .
 Pour tous nombres réels x et y strictement positifs :
ln x = ln y équivaut à x = y
ln x > ln y équivaut à x > y.
Propriété 6 (limites fondamentales)
lnx = 0
lim
x
x
lnx
lim
=0
x xn
lim
xlnx = 0
x0
lim
xn lnx = 0
x0
III . Fonction logarithme décimal
Définition 2
On appelle fonction logarithme décimal la fonction, notée log, définie sur l’intervalle
x .
 0 ; +   par log x = lnln10
Conséquences
log 1 = 0 et log 10 = 1
log est définie et strictement croissante sur l’intervalle  0 ; +   .

20
Propriété 7
Pour tous nombres a et b de l’intervalle  0 ; +   et tout nombre rationnel r :
log (a b) = log a + log b
log a = log a - log b
b
log ar = r log a
Conséquence
Soit x un nombre réel, si 10 n  x < 10 n +1 , alors n  log x < n + 1 .
IV. Fonctions exponentielles de base a
Définition 3
Pour tout nombre réel a strictement positif et tout nombre réel b, on pose : ab = eb lna .
Propriété 8
Pour tous nombres réels a et a’ strictement positifs et tous nombres réels b et b’ :
ln a b = b ln a
a b + b' = a b a b'
( a b )b' = a bb'
( a a' )b = a b a'b
ab
a b'
b
b
a = a
a'
a'b
a b - b' =
Définition 4
Soit a un nombre réel strictement positif et différent de 1.

On définit sur IR la fonction x a x par a x = exlna .
On l’appelle fonction exponentielle de base a.



21

CHAPITRE 7
INTEGRATION
I. Intégrale et primitive
Propriété 1
Soit une fonction f continue, positive sur l’intervalle  a ; b  et C sa courbe
représentative.
b
L’aire sous la courbe C représentative de f sur l’intervalle  a ; b ,  a f(x) dx , est égale
en unité d’aire, à F(b) – F(a) où F est une primitive de f sur l’intervalle  a ; b .
Soit une fonction f continue, négative sur l’intervalle  a ; b  et C sa courbe
représentative.
L’aire du domaine D limité par C, l'axe des abscisses et les droites d'équations x = a et
b
b
x = b est égale à  a  f(x) dx = -  a f(x) dx .
Remarques :

b
a
f(x) dx se lit :
On utilise la notation :
Intégrale de a à b de f
ou
Somme de f(x) dx de x = a à b

b
a
f(x) dx = F(x)a = F (b) – F (a)
b





Définition 1
Soit une fonction f continue sur un intervalle I et a un élément de I.
x
Pour tout x appartenant à I, la fonction définie par  a f(t) dt est l’unique primitive de
f sur I s’annulant en a.
22
Si F est une primitive quelconque de f sur I, alors

x
a
f(t) dt = F(x) - F(a) .
II. Propriétés algébriques de l’intégrale
Propriété 2 (relation de Chasles)
Soit une fonction f continue sur un intervalle I.
b
Quels que soient a, b et c éléments de I :  a f(x)dx =

c
a
f(x)dx +

b
c
f(x)dx .
Propriété 3 (linéarité de l’intégrale)
Soit deux fonctions f et g continues sur un intervalle I, a et b des éléments de I, et 
et  deux nombres réels, alors :
b
b
b
a ( f(x) +  g(x)) dx   a f(x) dx   a g(x)dx
Propriété 4 (fonctions paires et impaires)
Soit f une fonction continue sur un intervalle I centré en 0.
Pour tout élément a de I :
a
a
 Si f est paire : a f(x) dx  2  0 f(x) dx
 Si f est impaire :

a
a
f(x) dx  0
Propriété 5 (fonctions périodiques)
Soit f une fonction continue sur IR, périodique de période T.
aT
T
Pour tout nombre réel a :  a f(x) dx   0 f(x) dx .
III. Intégrales et inégalités
23
Propriété 6
Soit une fonction f continue positive sur un intervalle  a ; b  :

b
a
f(x) dx  0.
Propriété 7
Soit f et g deux fonctions continues sur un intervalle  a ; b  :

Si f  g , alors
b
a
f(x) dx 

b
a
g(x) dx .
Propriété 8
Soit une fonction f continue sur un intervalle I.
 Si les réels m et M sont tels que, pour tout x de l’intervalle I, on a m  f(x)  M , alors
si I =  a ; b  avec a < b :
m (ba) 

b
a
f(x) dx  M (ba)
Si le réel M est tel que, pour tout x de l’intervalle I, on a 0  f(x)  M , alors pour tous
les éléments a et b de I :
b
0  a f(x) dx  M ba .
Définition 2 (valeur moyenne)
Soit une fonction f , continue sur un intervalle
 a ; b . On appelle valeur moyenne
1  f(x) dx .
sur l’intervalle  a ; b  le nombre réel ba
b
de la fonction f
a
IV. Intégration par parties et changement de variable



Propriété 9
Soit u et v deux fonctions dérivables sur un intervalle I, telles que u’ et v’ soient
continues sur I.
Pour tous éléments a et b de I :

b
a
b
u(x) v'(x) dx  u(x) v(x)a 

b
a
u'(x) v(x) dx

Exemple : A = 0 2 x sinx dx = ? (Résultat : A = 1)
Propriété 10

Soit f et u deux fonctions dérivables sur un intervalle I, telles que u soit une bijection
sur I d’inverse u-1.Pour tous éléments a et b de I :


b
a
u ' ( x) f (u( x)) dx 

u (b )
u(a)
f (t ) dt
V. Intégrales doubles

La méthode générale de calcul de  D f(x,y) dx dy consiste donc :
- à intégrer d’abord par rapport à une variable, y par exemple, les bornes
dépendant de x
- puis à intégrer par rapport à l’autre variable.
24
On admet que, pour les fonctions continues, on peut intervertir l’ordre d’intégration
(Théorème de Fubini).
b
d
a
c

d
b
c
a

dx =   f (x , y) dxdy
 f (x, y) dx dy =  
 f (x , y) dy




D
Propriétés

DD'
f(x,y) dx dy 

D
f(x,y) dx dy 

f0
f g 

D

D


D'
f(x,y) dx dy si D et D’ sont disjoints.
D
f(x,y) dx dy  0
f(x,y) dx dy 
(af bg) (x,y) dx dy  a

D

D
f(x,y) dx dy  b
Exemple
Soit f (x, y) = x + 2 y , D = [0 , 1]  [0 , 1]
Calculons :
A=
g(x,y) dx dy
 D f (x , y) dx dy
(Résultat : A = 3/2)
25

D
g(x,y) dx dy
STIA 3
HARMONISATION
MATHEMATIQUES
Recueil d’exercices
26
CHAPITRE 1 : Généralités sur les fonctions
Exercice 1.1
Déterminer l’ensemble de définition des fonctions suivantes :
Exercice 1.2
Etudier la parité des fonctions suivantes :
Exercice 1.3
On considère un cercle C de centre O et de rayon 1. Soit I un point du cercle C et M un point
du segment [O ;I]. La perpendiculaire à la droite (OI) passant par M coupe le cercle C en A et
D. Construire les points C et B, symétriques respectifs des points A et D par rapport à O. On
note x=OM et f(x) l’aire du rectangle ABCD.
1/ Quel est l’ensemble de définition de la fonction f ?
2/ Donner l’expression de f(x)
3/ Pour quelle valeur de x l’aire du rectangle ABCD est-elle maximale ? Quel est ce
maximum ?
Exercice 1.4
La distance Paris-Reims est de 155 km par le rail. Le train de marchandises Paris-Reims
démarre de la gare de l'Est à 8h 30 min et roule à la vitesse moyenne de 60 km/h. Un express
part de Reims à 9h15 et roule à la vitesse moyenne de 90 km/h. À quelle heure et à quelle
distance de Paris les trains se croiseront-ils?
Exercice 1.5
On cherche à rénover une pièce de 4,20 m × 3,50 m dont la hauteur sous plafond est de 2,60
m. Les rouleaux de papier choisis pour tapisser le mur ont une longueur de 11,50 m et une
largeur de 50 cm. Chaque rouleau coûte 3,90 €. La peinture destinée à repeindre le plafond
coûte 5,50 € le pot. Chaque pot permet de peindre une surface de 8 m². La colle nécessaire
pour fixer le papier peint coûte 1,15 €.
1. Combien de rouleaux faut-il acheter ? (on néglige les chutes dues aux portes et fenêtres)
2. Quel est le coût des fournitures pour cette rénovation?
27
CHAPITRE 2 : Rappels de trigonométrie
Exercice 2.1
Simplifier :
cos (  - x) - cos ( + x) - sin ( + x) + sin ( - x)
2
2
Exercice 2.2
Déterminer en fonction de cos x et sin x l'expression de :
sin (x +  )
4
Exercice 2.3
Montrer que,  x  R ,
cos (x) + sin (x) = 2 sin ( + x) = 2 cos ( - x)
4
4
Exercice 2.4
Résoudre dans R les équations suivantes (donner les valeurs des solutions
appartenant à  - ; +  ] et placer les sur le cercle trigonométrique).
(1)
(2)
(3)
sin (2 x) = sin (  - 3 x)
4
cos (x) = cos ( - 3 x)
3

tan (x) = tan ( + 2 x)
2
28
CHAPITRE 3 : Limites et continuité
Exercice 3.1
A l'aide des opérations sur les limites, déterminer les limites suivantes :
lim - x2 (x + 2) - 1
lim x (x - 3)
x - 
x - 
lim x3 (1 - 1 + 43 )
x x
 
lim - x 3 x + 3
x
x - 
x - 
Exercice 3.2
Déterminer les limites en + ∞ et en - ∞ des fonctions suivantes définies sur lR :
g (x) = x 2 +1 - 1
h (x) =
x
2 + 3 x2
k (x) =
9 x3 + 1
x2 - 4 x + 5
Exercice 3.3
Calculer les limites suivantes :
lim x 2 + 4 x + 3 + x
x - 
Exercice 3.4
x 2 -4
x -2
1
1 - 2
lim
x 1 x - 1 x + 3
3x +5
lim
x 2


f (x) = 2 x + sin x
x
x +6 -3
lim
x 3
x -3
lim 2 x + 5
3x -2
1 - 2
lim
x 1 1 - x
1 - x2
x + 
lim
 x+5 -
lim
x
1 + x2 - 2
x  +
x 0

x- 3
Exercice 3.5
Calculer la limite de
x3 - 1
quand x  1 .
x2 - 1
Calculer la limite en + ∞ des fonctions définies ci-dessous :
f (x) = 2 x + sin x
x
Calculer la limite de
g (x) = x + 5 - x
x2 - x
h (x) = x 2 + 4 x + 3 - x
x2 + 2 x + 5 - x quand x  -  et quand x  + .
Exercice 3.6
Calculer la limite suivante de

Calculer la limite de
sin x - cos x
quand
x - / 4
x

4
x3 - 1
quand x  1 .
x2 - 1
Calculer les limites des fonctions suivantes quand x  0 :
sin x
g (x) = sin 2 x
x2 sin (1 )
sin 3 x
f ( x) =
x
h (x) =
sin x
x



29
CHAPITRE 4 : Dérivées et primitives
Exercice 4.1
Déterminer la dérivée de chacune des fonctions suivantes :
f ( x) = (4 - 3x) 3
g ( x) = (x 4  x 2  1) 3
h ( x) = (2x - 1) 2 (4 - 3x) 3
Exercice 4.2
Soit la fonction définie par
sa dérivée.
. Déterminez son domaine de définition puis calculez
En déduire les domaines et les dérivées des fonctions :
Exercice 4.3
Soit le polynôme :
Déterminer a, b et c pour avoir
. Montrer que le polynôme P se factorise par (x-2)3 et résoudre
l’équation P(x)=0.
Exercice 4.4
Déterminer une équation de la tangente à la courbe représentative de chacune des
fonctions ci-dessous au point d’abscisse a spécifié.
Exercice 4.5
Soit f la fonction définie sur
a) Montrer que  x 
 - 1 ; +  par : f ( x) = (2 x + 3 x - 2 x - 1)
2
f ( x) = 2 x - 1 + 2 ( x + 1)
 - 1 ; +  :
x +1
3
2
( x + 1) 2
2
b) Calculer les limites de f en – 1 et en + ∞.
c) Soit D la droite d'équation y = 2 x –1. Montrer que D est asymptote à la courbe de
représentative de f notée Cf et étudier la position de D par rapport à Cf.
x
d)
Déterminer
f'
et
f"
et
montrer
que
 - 1 ; + 
f ' ( x) = 2 x ( x 2 + 3 x + 4) ( x + 1) 3 et étudier les variations de la fonction f .
e) Montrer que la fonction f admet un minimum que l'on précisera et que l'équation
f (x) = 0 admet exactement deux solutions dans l'intervalle  - 1 ; + .
Exercice 4.6
Pour chaque fonction ci-dessous, déterminer le domaine de définition et calculer la
dérivée.
f (x) = ln
x2 + 1
g (x) =
Exercice 4.7
Etudier la fonction f (x) =
Montrer
que
1 + x 2 cos 2x
h (x) = cos ( x sin x )
x . Tracer sa courbe représentative.
x+1
pour
x >0
tout
30
:
x2
x< f (x) < x .
2
CHAPITRE 5 : Fonction exponentielle
Exercice 5.1 :
1 – Ecrire plus simplement :
2 – Résoudre les inéquations suivantes :
3 – Déterminer les limites suivantes :
Exercice 5.2 :
Calculer :
Exercice 5.3
Soit f la fonction définie par
. Sa courbe représentative dans un
repère orthonormal est noté C.
1 – Déterminer le domaine de définition de f et ses limites aux bornes de ce domaine.
2 – Montrer que la droite d’équation y=x+2 est asymptote à C en -∞ et préciser la
position de C par rapport à cette droite.
3 – Montrer que
et en déduire que la droite y=x-2 est asymptote
à C en +∞ en précisant à nouveau la position de C par rapport à cette droite-ci.
4 – Faites l’étude complète de f sur son domaine.
Exercice 5.4
Etudier le sens de variation de la fonction f définie par
que pour tout réel x :
31
En déduire
CHAPITRE 6 : Fonctions logarithmes
Exercice 6.1
Résoudre dans IR les équations suivantes :
ln x2 + 2 = 0
ln x2 + 2 x = ln 2 - x
ln x + ln x + 1 = 0
Exercice 6.2
Déterminer les limites ci-dessous.
ln x + 1
x+1
lim
ln ln x
x 1
ln x
lim
x 0 x - 2
lim
x  +
lim ln x
x+1
x  +
lim ln ln x
ln x
lim
x 2 x - 2
x  
lim ln x
x -2
x  
Exercice 6.3
 
a- Soit f la fonction définie sur 1 ; + par : f (x) = x ln 1 + 3 . Déterminer la limite de
x
f en +∞ puis interpréter graphiquement le résultat obtenu.
b- Pour tout x  1 ; + , calculer la dérivée première et la dérivée seconde de f .
Déterminer le sens de variation de f ' puis la limite de f ' en +∞. En déduire le signe
de f ' et indiquer les variations de f (tableau de variations).
Soit C la courbe représentative de f dans le plan muni d'un repère orthonormal
(O ; i ; j ) . Tracer la droite d'équation y = 3 et la courbe C en indiquant le point A de C
d'abscisse 3.
c - Soit g la fonction définie sur 1 ; + par : g (x) = x3+x3 et  sa courbe représentative.


Donner le tableau de variations de g .
Vérifier que, pour tout x de 1 ; +, on a : f (x) - g(x) = x f ' (x)
Déterminer le signe de f (x) - g(x) et la limite de f - g en + ∞.
Interpréter graphiquement les deux résultats. Tracer la courbe  dans le même repère
que C en indiquant le point B de  d'abscisse 3.
d - Soit  élément de 1 ; +.
Donner une équation de la tangente T à C au point d'abscisse .
Montrer que T rencontre (Oy) au point N d'ordonnée g ().
En déduire, à l'aide du tracé de , la construction de la tangente à C au point
d'abscisse .
Tracer de cette façon la tangente à C en A.
Exercice 6.4

On considère la fonction f définie sur IR par x ln (e-x + x) .
1.a- En étudiant les variations sur IR de la fonction u e-u + u , justifier que f peut
être définie sur IR.

1.b- En déduire que, pour tout x  IR, 1 + x ex > 0
1.c- Vérifier que, pour tout x  IR, on a : f(x) = ln (1 + xex) - x
32
2- Calculer f’(x) et étudier les variations de f sur IR.
f(x)
3.a- Calculer lim
x
3.b- Montrer que lim
f(x) + x = 0 .
x-
3.c- Montrer que, pour tout x  0 : f(x) + x  0.
4- On définit, sur un intervalle  0 ; +   , la fonction g par g (x) = f (x) - ln x
4.a- Etudier la limite de g en + ∞
4.b- Etudier le signe de g sur l’intervalle  0 ; +  
Exercice 6.5
Calculer les dérivées suivantes :
f (x) = x ln (x)

f (x) = ln x + x2 + 1
f (x) = ln ln x

Exercice 6.6
Etudier les fonctions :
f (x) = ln (1 + x) - x
g (x) = ln (1 + x) - x +
En déduire que, si x > 0, on a : x -
x2
2
x2
< ln (1 + x) < x .
2


33
h (x) = x - 1 - ln x
CHAPITRE 7 : Intégration
Exercice 7.1
Calculer l'aire sous les courbes des fonctions suivantes sur les intervalles donnés.
f (x) = x3
[0 ; 1]
[1 ; 2]
g (x) = - 1
x
Exercice 7.2
Calculer : A =
 03  2 - t + 1 - t dt
Exercice 7.3
Calculer les intégrales suivantes :
A=
 01 x22+xx++13 dx

D=

6
sin 3x dx
1
 x + 1 ex
B=
2
+ 2x + 1
dx C =
0
0
 x (2 x2 + 1) dx
E=

F=
-1
0
1
 x22 -x4 dx
0
4
1
dx
2 x+ 1
0
Exercice 7.4
Soit f une fonction définie par f (x) =
x2 + 2 x - 1
sur 3 ; +  . Déterminer les réels a,
x+3
Exercice 7.5
Soit f une fonction définie par f (x) =
6x -3
 f (x) dx
2
x + 2 x - 1
2
Déterminer les réels a et b tels que : f (x) =
Calculer
2
c . Calculer
x + 3
b et c tels que : f (x) = a x + b +
2
sur 2 ; 1.
a
b .
2 +
2
x + 2 x - 1
0
 f (x) dx .
1
Exercice 7.6
A l'aide d'une intégration par parties, calculer les intégrales suivantes :

1

e

1
x e-x dx
e
2
 x cos x dx
0
2
ln x dx
x2
1
 (x + 1) e - 2x dx
1
 ln x dx
1
2
 x2 ln x dx
1
Exercice 7.7
L'objectif principal de cet exercice est de calculer l'intégrale I =

34

0
1
x ex
1 + ex
3
dx .
a- calculer les intégrales A et B
A=
ex
1
 1 + ex dx
0
B=
et

0
1
ex
dx
1 + ex
2
b- Pour tout nombre t positif ou nul , déterminer a, b et c tels que :
(1)
1 =a+ bt + ct
2
1 + t 1 + t2
1 + t
En posant t = ex dans l'égalité (1), calculer l'intégrale J =

0
1
ex
1 + ex
2
dx .
c- A l'aide d'une intégration par parties, exprimer I en fonction de J. En déduire
la valeur de I.
Exercice 7.8 : Calculer

f (x , y) dx dy si :
D
f (x , y) =
f (x , y) = e
1
2
1 + x + y
x2
f (x , y) = x - y
f (x , y) =
1 dx dy
(x + y) 4
D = 1 ; 2  1 ; 2

D = (x , y)  IR2 : 0  x  3 , 0  y  x
3
D = (x,y)  R2 / x  1 et y  1

D = (x , y)  R2 / x  1, y  2, x + y  5
35
CHAPITRE 8 : Equations différentielles linéaires du premier ordre
Exercice 8.1
Déterminer la solution f sur IR des équations différentielles suivantes vérifiant la
condition donnée :
y' =2y
f ( 3) = - 2
3y ' =-6y
f ( -4) = 2
5y ' +y =0
f (-5) = 1
2 y - 5 y' = 0
f (1) = - 3
Exercice 8.2 *
Déterminer la solution f sur IR des équations différentielles suivantes vérifiant la
condition donnée :
3 y '- y =1
f (0) = 2
y ' =3y -2
f (0) = 1
y ' -5y =3
f (0) = 2
Exercice 8.3
A l’instant t=0 (t exprimé en minutes), on injecte dans un réacteur parfaitement
mélangé une dose de 2 unités d’une substance colorée. La substance colorée se
répartit instantanément dans le réacteur et elle est ensuite progressivement éliminée.
On note Q(t) la quantité de substance présente dans le réacteur à l’instant t, exprimée
en unités adaptées.
On admet que le processus d’élimination peut se représenter mathématiquement par
l’équation différentielle : Q’ (t) = -  Q (t), où  est un nombre qui sera déterminé
expérimentalement.
1-Exprimer Q (t) en fonction de t et . Au bout d’une minute, la quantité de substance
présente dans le réacteur a diminué de 25 %.
2-Déterminer la valeur de 
3-Etudier le sens de variation de Q pour t 0.
Exercice 8.4
Déterminer la solution générale des équations différentielles suivantes :
(1) y ' - 2 y = - 3 - 4 x + 2 x2
(2) 2 y ' + y = - x 2 6 + x
(3) y ' - 5 y = - 5 - 2 x + 5 x2
Exercice 8.5
Déterminer la solution générale des équations différentielles suivantes :
(1)
(2)
x y ' +2 y =x2 - 3
2 y ' - y = exp ( x)
36