Corrig´es de la s´eance 5 Chap 4: Dynamique

Corrig´ es de la s´ eance 5
Chap 4: Dynamique
Questions pour r´ efl´ echir
[4] Jupiter a une masse 318 fois plus grande que celle de la Terre. Pour-
tant, l’acc´ el´ eration de la pesanteur ` a sa surface est seulement de 26 m/s2.
Pourquoi ?
La densit´ e (masse volumique) de Jupiter est bien plus faible que celle de la Terre.
On a, ` a la surface de toute plan` ete P:
gP=GMP
R2
P
⇒gJ
gT
=26
10 =MJ
R2
J
R2
T
M2
T
= 316R2
T
R2
J
⇒RT
RJ
= 0.091 .
Or la masse volumique est donn´ ee par ρP=MP/VPo` uVP= 4πR3
P/3donc
ρJ
ρT
=MJ
R3
J
R3
T
MT
= 316 ×(0.091)3= 0.24 .
[8] Le Soleil semble se d´ eplacer par rapport aux ´ etoiles plus rapidement en
hiver qu’en ´ et´ e. Que peut-on en d´ eduire concernant la distance de la Terre
au Soleil ` a ces deux p´ eriodes de l’ann´ ee ?
Par application de la loi des aires, la Terre se trouve donc plus pr` es du Soleil en
hiver qu’en ´ et´ e (la diff´ erence de temp´ erature dans l’h´ emisph` ere Nord entre hiver et
´
et´ e est due ` a l’inclinaison de l’axe de la Terre, pas ` a sa proximit´ e du Soleil).
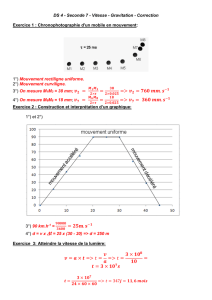
[13] La figure ci-dessous montre une manoeuvre qu’une fus´ ee peut ef-
fectuer pour s’ ´ echapper d’une orbite circulaire autour d’une plan` ete vers
une trajectoire hyperbolique, quelle parcourt sans propulsion. Que faut-il
faire en A ? Si le processus a lieu en sens inverse, le vaisseau arrivant en
chute libre vers la plan` ete, que faut-il faire pour passer en orbite circulaire
?
1

Pour s’´ echapper, il faut donner une acc´ el´ eration tangentielle dirig´ ee dans le sens de
la vitesse, de fac¸on ` a augmenter la vitesse tangentielle de la fus´ ee jusqu’` a atteindre
la vitesse de lib´ eration. Pour passer en orbite circulaire, il faut exercer une pouss´ ee
tangentielle dans le sens oppos´ e` a la vitesse.
Exercices
1. [1-I] Que deviendrait le poids d’un objet si sa masse ´ etait doubl´ ee et sa
distance au centre de la Terre ´ egalement doubl´ ee ?
Le poids d’un objet est donn´ e par
P=GmMT
d2.
Si la masse et la distance sont doubl´ ees, le num´ erateur est multipli´ e par 2, le
d´ enominateur par 4 donc le poids est divis´ e par 2.
2. [4-I] A quelle distance du centre de la Terre une masse de 1,0 kg p` ese-
t-elle 1,0 N ?
g
g′=9,81 1,0=GMT/R2
T
GMT/d2⇒9,81 = d2
R2
T
⇒d=p9,81RT
.
(3.) [11-I] Les masses des ´ electrons et des protons sont respectivement
9,1×10−31 kg et 1,7×10−27 kg. Lorsqu’ils sont distants de 5,3×10−11 m,
comme dans l’atome d’hydrog` ene, ils s’attirent avec une force ´ electrique
FEde 8,2×10−8N. Comparez cette force avec l’attraction gravitationnelle
correspondante FG. Quel est le rapport entre FEet FG?
La force gravitationnelle est donn´ ee par
FG= 6,67.10−11 ×9,1.10−31 ×1,7.10−27
(5,3.10−11)2= 3,7.10−47 N
soit 2,2.1039 fois plus faible que l’attraction ´ electrique.
(4.) [18-II] Sachant que ML/MT= 0,01230 et RL/RT= 0,2731, calculer le
rapport du poids d’un astronaute sur la Lune ` a son poids sur la Terre.
Le poids d’un corps de masse m` a la surface du corps c´ eleste C est donn´ e par
PC=GmMC
R2
C
⇒PL
PT
=ML/R2
L
MT/R2
T
=ML
MTRT RL2
= 0,16 .
2

5. [20-II] D´ eterminez la position d’un vaisseau spatial sur la droite joignant
les centres de la Terre et de la Lune, o` u les forces exerc´ ees sur lui par
ces deux corps c´ elestes sont exactement oppos´ ees. Le vaisseau est alors
sans poids.
Lorsque les deux forces d’attraction se compensent exactement, on a
GmV
MT
d2
T
=GmV
ML
d2
L
.
Soit xla distance entre le vaisseau et la Terre, et Dla distance Terre-Lune
⇒MT
d2
T
=ML
d2
L
⇒(D−x)2
x2=ML MT
⇒D−x
x=D x−1 = rML MT
⇒D
x= 1 + rML MT
⇒x=D
1 + qML
MT
.
Comme MLest inf´ erieure ` aMT, le d´ enominateur est inf´ erieur ` a 2 et x > D/2: ce
point est plus proche de la Lune que de la Terre.
(6.) [22-II] Trois tr` es petites sph` eres, de masses respectivement 2,50 kg,
5,00 kg et 6,00 kg, sont situ´ ees sur une ligne droite dans l’espace, loin de
tout autre corps. La premi` ere masse est situ´ ee entre les deux autres, ` a
10,0 cm ` a droite de la seconde, et ` a 20,0 cm ` a gauche de la troisi` eme.
Calculer la force gravitationnelle subie par la premi` ere sph` ere.
La force gravitationnelle ~ FCs’exerc¸ant sur la sph` ere C est la r´ esultante des forces
~
FAC et ~ FBC . Cette force est dirig´ ee selon l’axe BA et son module est donn´ e par
FC=FAC −FBC =GmCmA
d2
AC
−mB
d2
CB 
= (6,67.10−11N.kg−2.m2)×(2,50kg)500kg.m−2−150kg.m−2
= 58,4.10−9N
3

7. [45-I] Un satellite doit passer d’une orbite circulaire ` a une autre de rayon
deux fois plus grand. Comment sa p´ eriode est-elle modifi´ ee ?
La force centrip` ete qui maintient le satellite sur son orbite circulaire est l’attraction
gravitationnelle. On a donc
mω2R=GmMT
R2⇒ω2R3=GMT= Cte
avec ω= 2π/T o` uTest la p´ eriode. Nous obtenons ainsi la deuxi` eme loi de Kepler
⇒R3
T2= Cte .
Si Rest multipli´ e par 2, la p´ eriode est donc multipli´ ee par 23/2= 2,8.
8. [50-II] Par d´ efinition, la Terre est ` a une distance de 1,0000 UA (unit´ e
astronomique) du Soleil. Utilisant le fait que Jupiter est, en moyenne, ` a
5,2028 UA du Soleil, calculez sa p´ eriode en ann´ ees terrestres.
D’apr` es la deuxi` eme loi de Kepler, T2/R3est une constante, la mˆ eme pour la Terre
et pour Jupiter. Prenons comme unit´ es l’ann´ ee terrestre et l’UA. Nous avons
(1an)2
(1UA)3=T2
J
R3
J
⇒TJ
1an =sRJ 1UA3
=p5,20283= 11,867 .
La p´ eriode de Jupiter autour du Soleil est de 11,867 ann´ ees terrestres.
9. [33-III] Une ´ etoile ` a neutrons, de masse de l’ordre de celle du Soleil et
d’un rayon d’environ 10 km, est en fait un immense noyau atomique, soud´ e
par sa propre gravitation. Quelle est la p´ eriode de rotation de cette ´ etoile
au-dessous de laquelle elle ´ ejecte de la mati` ere ´ equatoriale ? Prendre
ρ= 1017 kg / m3.
Il faut que l’attraction gravitationnelle soit insuffisante pour assurer la force cen-
trip` ete n´ ecessaire (si on se place dans le r´ ef´ erentiel en rotation: que la “force cen-
trifuge” soit plus grande que la force gravitationnelle), donc que
GmM
R2< mω2R⇒ω2>GM R3.
Avec ω= 2π/T et ρ=M/V =M/(4πR3/3) ⇒M/R3= 4πρ/3, nous
obtenons
ω=2π
T>r4π 3Gρ ⇒T < 2π
p4πGρ/3=2π q4π
3×6,67.10−11.1017
4

⇒T < 1,2.10−3s.
(10.) [59-III] Io, l’une des quatre lunes de Jupiter d´ ecouvertes par Galil´ ee
en 1610, a une p´ eriode de 1,7699 j (jours terrestres), et elle est ` a une
distance de 5,578 RJ(rayons de Jupiter) du centre de la plan` ete. En
d´ eduire la densit´ e moyenne (masse volumique) de Jupiter. Prenez G=
6.67259 ×10−11 N m2kg−2.
La force centrip` ete qui maintient Io sur son orbite circulaire est l’attraction gravi-
tationnelle. On a donc, en appelant dla distance moyenne entre Io et Jupiter:
mIo ω2d=GmIoMJ
d2⇒ω2=GMJ d3=GMJ (5,578RJ)3.
Comme ω= 2π/T et ρJ=MJ/VJ=MJ/(4πR3
J/3) ⇒MJ/R3 J= 4πρJ/3, on
a
(2π)2
T2=G4π 3ρJ
1
5,5783⇒ρJ=(2π)2 T2
3
4πG(5,5783)⇒ρJ= 1048,3 kg.m−3.
Remarque : (GT 2)s’exprime en N.kg−2.m2.s2=kg.m.s−2.kg−2.m2.s2donc 1/(GT 2)
a pour dimensions kg.m−3.
6. [I] p.227. Un enfant de 200 N est debout, au repos, sur un plan inclin´ e
d’un angle de 24◦par rapport ` a l’horizontale. Calculer la force de frottement
sur ses chaussures. Quelle doit ˆ etre la valeur minimum de µs?
D´ ecomposons ~ Pdans les directions k(sens positif vers le bas du plan) et ⊥au
plan inclin´ e (sens positif vers le haut). Imposons les conditions d’´ equilibre dans
ces deux directions:
k:Psin θ−Ff= 0
⊥:−Pcos θ+N= 0.
Puisqu’il n’y a pas de glissement, il faut Ff< F max
f=µsN, c’est-`
a-dire Psin θ <
µsPcos θ. Donc µs>tan θ= 0,445.
(69.) [I] p.191. Un camion transporte une caisse de bois de masse 50,0 kg.
Il aborde une mont´ ee d’inclinaison 20,0◦. Y a-t-il un risque que la caisse
commence ` a glisser, si le camion roule ` a vitesse scalaire constante et le
coefficient de frottement statique de la caisse sur la plate-forme du camion
est 0,3 ?
5