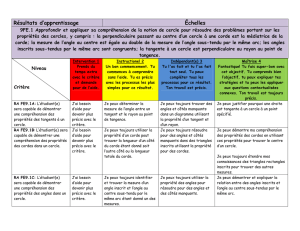
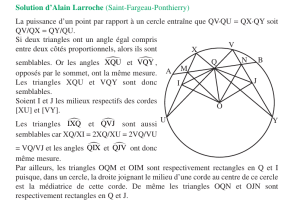
Énoncé - Site de JJ Thiry
Puma
Aurélie
2ème math
Énoncé :
Soit un cercle de centre O.
oo
Énoncé :
Soit un cercle de centre O.
M est le milieu d’une corde [PQ] de ce cercle.
oo
PQ
M
Énoncé :
Soit un cercle de centre O.
M est le milieu d’une corde [PQ] de ce cercle.
[AB] et [CD] sont des cordes passant par le point M.
oo
PQ
M
A
B
C
D
Énoncé :
Soit un cercle de centre O.
M est le milieu d’une corde [PQ] de ce cercle.
[AB] et [CD] sont des cordes passant par le point M.
[AD] coupe [PQ] en X et [BC] coupe [PQ] en Y.
oo
PQ
M
A
B
C
D
XY
6
7
8
9
10
11
12
13
14
15
16
1
/
16
100%
