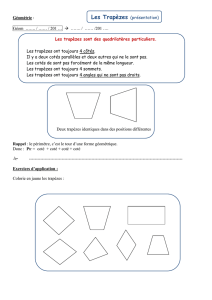
Preuve de la méthode des trapèzes - Blogdemaths

Méthode des trapèzes
—
Estimation de l’erreur
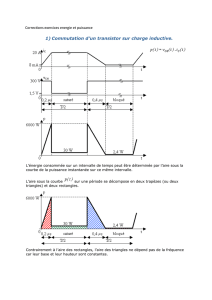
Soit fune fonction de classe C2sur un intervalle [a,b](c’est-à-dire deux fois
dérivable et de dérivée seconde continue sur [a,b]) dont on cherche l’aire sur
[a,b]. Soit n>0 un entier et x0=a<x1<x2<· · · <xn=bune subdivi-
sion régulière de [a,b](c’est-à-dire telle que pour tout i,xi+1−xi=b−a
n. La
méthode des trapèzes consiste à remplacer fsur chaque intervalle [xi,xi+1]par
une fonction affine :
f(x)
x0=a x1xixn=b xi+1
Tn
On note Tnla somme des aires de tous les trapèzes. Nous allons présenter une
démonstration du fait que la suite Tntend bien vers Rb
af(x)d x et que l’erreur
commise Rb
af(x)d x −Tnest au plus M(b−a)3
12n2(où Mest une constante dépen-
dant de f).
1 On encadre l’erreur sur chacun des intervalles [xi,xi+1]
On commence par se placer sur l’intervalle [xi,xi+1]. La fonction affine fiqui va
remplacer fest l’unique fonction affine fitelle que fi(x) = f(xi)et fi(xi+1) =
f(xi+1). L’expression de fiest donc
fi(x) = f(xi) + f(xi+1)−f(xi)
xi+1−xi
(x−xi)
Cette fonction affine qui coïncide avec la fonction fen xiet xi+1s’appelle aussi
le polynôme interpolateur de Lagrange de f. Ce qui est bien avec les polynômes
1

interpolateurs de Lagrange, c’est qu’on sait donner exactement l’erreur commise.
Plus précisément, on peut montrer que
Lemme. Pour tout x ∈[xi,xi+1], il existe un réel cx∈[xi,xi+1]tel que
f(x)−fi(x) = (x−xi)(x−xi+1)f00(cx)
2
Démonstration. Soit x∈[xi,xi+1]fixé. Si x=xiou x=xi+1, la propriété est évidem-
ment vraie car dans ce cas f(x)−fi(x) = 0 et n’importe quel nombre c∈[xi,xi+1]
convient. Nous pouvons donc supposer xdifférent de xiet de xi+1.
Introduisons la fonction définie sur [xi,xi+1]par
g(t) = f(t)−fi(t)−(t−xi)(t−xi+1)
(x−xi)(x−xi+1)f(x)−fi(x)
Pourquoi cette fonction ? Parce qu’elle s’annule en xi, en xet en xi+1. Ainsi, d’après le
theorème de Rolle :
– Comme g(xi) = 0=g(x), il existe c1∈]xi,x[tel que g0(c1) = 0
– Comme g(x) = 0=g(xi+1), il existe c2∈]x,xi+1[tel que g0(c2) = 0
Ainsi, la fonction g0s’annule deux fois (en c1et c2), donc une nouvelle application du
theorème de Rolle nous donne l’existence d’un réel cxtel que g00(cx) = 0.
D’autre part, calculons, pour tout t∈[xi,xi+1],g00(t). Tout d’abord, f00
i(t) = 0 car fiest
une fonction affine. Ensuite, l’expression (t−xi)(t−xi+1)
(x−xi)(x−xi+1)f(x)−fi(x)est un polynôme
du second degré en t. Son monôme de plus haut degré est t2
(x−xi)(x−xi+1)f(x)−fi(x)
et on voit qu’en dérivant 2 fois ce monôme, on obtient 2 [f(x)−fi(x)]
(x−xi)(x−xi+1). Ainsi,
g00(t) = f00(t)−0−2f(x)−fi(x)
(x−xi)(x−xi+1)
De la relation g00(cx) = 0 on tire que 0 =f00(cx)−2[f(x)−fi(x)]
(x−xi)(x−xi+1), ce qui donne bien
f(x)−fi(x) = (x−xi)(x−xi+1)f00(cx)
2
Du lemme précédent, on déduit que pour tout x∈[xi,xi+1]:
|f(x)−fi(x)|¶|x−xi|.|x−xi+1|M
2= (x−xi)(xi+1−x)M 2
où Mest un majorant de |f00|sur l’intervalle [xi,xi+1]. Ainsi, la différence entre
l’aire de la fonction et l’aire du trapèze est majorée par
Zxi+1
xi
f(x)−fi(x)d x ¶M
2Zxi+1
xi
(x−xi)(xi+1−x)d x
Cette dernière intégrale peut se calculer à l’aide du changement de variable affine
x=xi+ (xi+1−xi)u⇔u=x−xi
xi+1−xi:
2

Zxi+1
xi
(x−xi)(xi+1−x)d x =Z1
0
(xi+1−xi)u(xi+1−xi)(1−u)(xi+1−xi)du
= (xi+1−xi)3Z1
0
u(1−u)du
= (xi+1−xi)3u2
2−u3 31
0
=(xi+1−xi)3
6
Ainsi, nous avons l’inégalité suivante :
Zxi+1
xi
f(x)−fi(x)d x ¶M
2
(xi+1−xi)3
6=M(xi+1−xi)3 12
Nous avons donc prouvé
Proposition. Soit f une fonction de classe C2sur un intervalle [xi,xi+1]. Soit fi
la fonction affine qui coincide avec f en xiet xi+1. Alors
Zb
a
f(x)−fi(x)d x ¶M(xi+1−xi)3
12
où M est un majorant de |f00|sur [xi,xi+1].
Dans toute la suite, nous prendrons M=supx∈[a,b]|f00(x)|. Rappelons que notre
subdivision (xi)iétait telle que xi+1−xi=b−a
n. D’où :
Zxi+1
xi
f(x)−fi(x)d x ¶M(b−a)3
12n3
2 On encadre l’erreur globalement
L’erreur globale se calcule en faisant la somme des erreurs :
Zb
a
f(x)d x −Tn=
n−1
X
i=0Zxi+1
xi
f(x)−fi(x)d x
3

Ainsi,
Zb
a
f(x)d x −Tn ¶
n−1
X
i=0Zxi+1
xi
f(x)−fi(x)d x
¶
n−1
X
i=0
M(b−a)3
12n3
¶M(b−a)3
12n3
n−1
X
i=0
1
¶M(b−a)3
12n3×n=M(b−a)3 12n2
Comme la limite quand ntend vers l’infini de M(b−a)3
12n2vaut 0, cela veut bien dire
que l’aire des trapèzes tend vers l’aire de la courbe. Le méthode des trapèzes
permet donc bien d’approcher l’aire totale !
Voici résumé ce que nous avons prouvé :
Proposition. Si f est une fonction de classe C2sur un intervalle [a,b], et si on
pose M =supx∈[a,b]|f00(x)|alors
Zb
a
f(x)d x −Tn ¶M(b−a)3
12n2
4