GLPH311 - Electrostatique et Magnétostatique Examen de 1

GLPH311 - Electrostatique et Magnétostatique
Examen de 1ère session, le 8 janvier 2014
Durée 2 heures, aucun document autorisé,
calculatrice et téléphone portable interdits
Soyez clair, concis et apportez le plus grand soin à la rédaction
On rappelle : µo/4=10-7 S.I.
Partie 1 - électrostatique : (10 pts) :
Soit une plaque d'un matériau non-conducteur
d’épaisseur 2a, considérée comme un plan infini et
placée dans l'espace parallèlement au plan xOy. La
plaque est disposée symétriquement par rapport au plan
z=0 et elle porte une charge électrique positive non
uniformément répartie. La densité volumique de charge
au sein de la plaque est représentée par la fonction
suivante :
ooo azz
a
 :poseon ici;pour )
2
cos(
1. Illustrer sur un graphique les variations de la densité volumique de charge (z) dans tout l’espace.
Décrire ses invariances et en déduire les variables dont dépend le champ électrique qui en résulte.
2. Décrire tous les éléments de symétrie de cette distribution de charge : plans de symétrie et
d’antisymétrie. En déduire la direction puis le sens du champ électrique
)(ME
crée par cette
distribution de charges en un point M quelconque de l’espace repéré par ses coordonnées
cartésiennes (x,y,z).
3. On cherche à établir, à l’aide du théorème de Gauss, l’expression du champ électrique
)(ME
en
tout point de l’espace.
3.1 Soit une boite imaginaire cylindrique d’axe Oz et de
surface latérale S3, possédant deux faces parallèles au
plan xOy, situées aux hauteurs z et –z comme
indiqué sur la figure (on notera S1=S2=S l’aire de ces
faces). Exprimer le flux du champ électrique à travers
cette boite imaginaire en fonction de l’amplitude du
champ à la hauteur z, E(z), et de l’aire S.
3.2 Calculer la charge électrique Qint située dans le volume intérieur de la boite en fonction de
o, a, S et z. On distinguera les deux cas |z| <a et |z|>a.
3.3 Utiliser les résultats précédents pour obtenir les expressions du champ électrique à
l’extérieur (|z|>a) et à l’intérieur (|z|<a) de la plaque chargée, respectivement
)(zEext
et
)(
int zE
.
3.4 Illustrer sur un graphique l’allure des variations de l’amplitude du champ en fonction de la
hauteur z.
3.5 Vérifier que l’équation locale de Gauss satisfait bien votre résultat
)(
int zE
.

4. Établir l’expression du potentiel électrique V(M) engendré par cette distribution de charge au point
M(x,y,z) tel que z > a. On prendra comme condition de bord : V(z = +a ) = 0 volt.
5. Que vaut la circulation du champ
E
le long de l'axe Oz entre z a et z=2a ?
Partie 2 - magnétostatique (10 pts):
On considère un fil conducteur cylindrique infini d’axe Oz et de rayon Ro. Le fil est parcouru
par un courant stationnaire I circulant dans le sens des z croissants. La densité de courant est
uniforme et s’écrit
z
ejMj  )(
pour tout point M à l’intérieur du fil.
1. On donne : Ro=0,1 cm et
5
10
j
A/m². Calculer la valeur de l’intensité I du courant qui parcourt
le fil.
2. Les éléments de symétrie et les invariances du système :
2a. Décrire les plans de symétrie et d’antisymétrie de la distribution de courant
j
en vous aidant
d’un schéma.
2b. Quel est le système de coordonnées le mieux adapté à la description de cette distribution ?
Représenter sa base orthonormée locale en un point M quelconque de l'espace.
2c. Déduire des éléments de symétrie de
j
la direction du champ magnétique
)(MB
créé en tout
point M de l'espace.
2d. Décrire les invariances de
j
et en déduire celles du champ
)(MB
. En déduire les variables
dont dépend le champ magnétique B.
3. Les expressions du champ magnétique
)(MB
:
3a. Exprimer la circulation du champ magnétique, le long d’un contour circulaire d’axe Oz et de
rayon r passant par un point M quelconque de l’espace.
3b. Exprimer le flux du champ
j
à travers la surface délimitée par ce contour circulaire en
distinguant les deux cas rRo et r>Ro. (indiquer clairement comment vous orientez la surface
d’intégration).
3c. Utiliser les résultats précédents pour obtenir les expressions du champ magnétique à l’extérieur
et à l’intérieur du fil, respectivement
)(MBext
et
)(
int MB
.
3d. Illustrer sur un graphique l’allure des variations de l’amplitude du champ B(r) en fonction de
la distance r à l’axe du fil. Faire un schéma illustrant la forme des lignes de champ en
indiquant bien leur orientation.
3e. Calculer l’amplitude du champ au point M ( r= 2 cm, /3 rad, z= 125 cm).
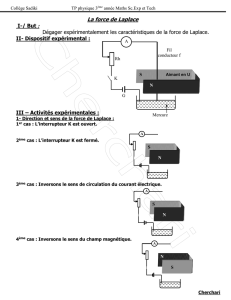
4. La force de Laplace :
4a. On place un second fil conducteur parallèle au premier et à une distance d>Ro de celui-ci. Les
fils n°1 et n°2 sont parcourus par un courant de même intensité mais de sens opposé. Chaque
fil est soumis à la fois à son propre champ magnétique et au champ créé par le second fil.
Quel champ intervient-il dans la force de Laplace : le champ propre, le champ appliqué ou la
somme des deux ? Illustrer sur un schéma le vecteur de la force de Laplace qui s’exerce sur le
fil conducteur n°1.
4b. On supprime le second fil et on place le fil conducteur n°1 sur l'axe d'un solénoïde considéré
comme infini. Le solénoïde est caractérisé par son rayon R>Ro et la densité de spires jointives
n. Il est parcouru par un courant stationnaire d’intensité Io. Calculer la force exercée par ce
solénoïde sur le fil conducteur.