Nombres relatifs en écriture fractionnaire

Chapitre 3 : Nombres en écriture fractionnaire
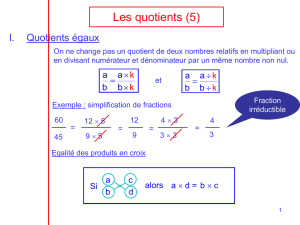
1- Egalité de quotients
a) Propriété des quotients égaux
Propriété(admise) :On ne change pas le quotient de deux nombres relatifs en multipliant
ou en divisant son numérateur et son dénominateur par un même nombre relatif non nul.
a, b et k désignent des nombres relatifs, b = 0 et k = 0.
On a :
kb ka b
a
et
kb ka b
a
Exemples :
5
7
27
18
18
24
Propriété
a et b désignent des nombres relatifs avec
0b
.
On a :
b
a
b
a
ba
et
b
a
b
a
Exemples : 
38
5
7
b) Egalité des produits en croix
Propriétés : a, b, c et d désignent des nombres relatifs, avec
0b
et
0d
 Si
d
c
b
a
, alors
cbda 
 Si
cbda 
alors
d
c
b
a
Exemple : On veut savoir si les quotients
21
1,5
14
1,3 et
sont égaux.
 211,3
 1,514
. On constate que .
Donc

2- Addition et soustraction.
a) Les dénominateurs sont égaux
Propriétés(admises)
a, b, c désignent des nombres relatifs, avec
0b
.
Pour additionner deux nombres relatifs en écriture fractionnaire de même dénominateur :
 On garde le dénominateur commun
 On additionne les numérateurs
bca b
c
b
a
Pour soustraire deux nombres relatifs en écriture fractionnaire de même dénominateur :
 On garde le dénominateur commun
 On soustrait les numérateurs
bca b
c
b
a
Exemples : 
5
8
52
 75,2
7
3,1
b) Les dénominateurs sont différents
METHODE : Pour additionner ou soustraire deux nombres relatifs en écriture
fractionnaire de dénominateurs différents, on commence par les mettre au même
dénominateur.
Exemples :
15
7
34
A
7
9
4
5B
29 6
5
C
15
13
15 720 15
7
15
20 15
7
53 54 15
7
34
A
A
A
A
A

3 – Multiplication
Propriété : Pour multiplier deux nombres relatifs en écriture fractionnaire :
 On détermine le signe du produit
 On multiplie les numérateurs entre eux
 On multiplie les dénominateurs entre eux
a, b, c et d désignent des nombres relatifs avec b  0 et d  0.
Produit des numérateurs
db ca d
c
b
a
Produit des dénominateurs
Remarque : Pour déterminer le signe d’un produit de nombres relatifs en écriture
fractionnaire, on utilise la « règle des signes » étudiée au chapitre 2.
Exemples :
7
8
35
D
9)2( 5
3,2
E
9
8
5 F
Conseil : Pour multiplier des nombres relatifs en écriture fractionnaire, il est préférable de
déterminer le signe du produit en comptant les signes négatifs) et de simplifier avant de
multiplier.
Exemple :
20
3
543 5544 345 2516 125 25
12
16
5

4 - Division
a) Inverse d’un nombre non nul
Définition : L’inverse d’un nombre relatif a non nul est le nombre qui multiplié par a donne 1
Exemples :
 -25 x (-0,04) = 1. Donc -25 est l’inverse de -0,04 et -0,04 est l’inverse de -25.
 5 x 0,2 = 1. Donc 5 et 0,2 sont deux nombres inverses.
! Attention le nombre 0 n’a pas d’inverse.
Propriété : a désigne un nombre relatif, avec a0.
L’inverse du nombre a est le nombre
a
1
.
Ainsi
1
1 a
a
Exemple : L’inverse du nombre -5 est le nombre
5
1
, c’est à dire
5
1
.
Propriété : a et b désignent deux nombres relatifs, avec a  0 et b  0.
L’inverse du nombre
b
a
est le nombre
a
b
.
Exemple : L’inverse du nombre
35,2
est le nombre
5,23
.
b)Quotient de deux nombres relatifs
Propriétés : Diviser par un nombre non nul revient à multiplier par son inverse.
a et b désignent des nombres relatifs, avec b  0. On a
b
aba 1
a, b, c et d désignent des nombres relatifs non nuls . On a
c
d
b
a
d
c
b
a
Exemples :
6
1
2
3
2
1
35,03 
35
12
57 34 5
3
7
4
3
5
7
4
Conseils :
Ne pas confondre l’inverse d’un nombre et l’opposé d’un nombre

Exemple : Le nombre 3 a pour opposé -3 et pour inverse
3
1
.
c
d
b
a
d
c
b
a
d
c
b
a
Exemple :
21
10
73 52 7
5
32 5
7
32
5
7
32