Construire par pliage des polygones réguliers avec un nombre

Construire par pliage des polygones réguliers
avec un nombre impair de côtés, c’est
possible, simplement! (Partie 1)
Antoine Trottier, étudiant au BES1 en mathématiques à l’UQAM
[e-mail]
L’article suivant est séparé en deux et paraîtra donc, dans
deux numéros consécutifs. La première partie présente
les exposés types proposés aux étudiants du baccalauréat
en enseignement de la mathématique au secondaire à
l’UQAM. La seconde partie présentera un nouvel exposé
type concernant les polygones par pliage avec un nombre
impair de côtés.
Pourquoi, au départ avoir choisi l’UQAM pour faire mes
études? C’est la campagne de publicité EFFET UQAM
qui m’a fait connaître cette université. On voyait des
affiches partout, dans les rues, sur les autobus et dans les
métros présentant une université active et dynamique.
Je cherchais comme futur enseignant au secondaire
exactement ce type de formation, axée sur la pratique. À
vrai dire, je souhaitais me retrouver sur les affiches de
l’EFFET UQAM, je voulais représenter cette université.
Mais comment? Le fait d’avoir des A dans toutes mes
matières n’allait certainement pas être suffisant. C’est
dans un cours de didactique dispensé durant la deuxième
session de la première année du BES que la chance m’a
souri, ce cours allait peut-être me permettre de laisser une
légère trace de mon passage dans cette université.
Dans un des volets du cours, Didactique 1 et laboratoire
(MAT2024), nous visionnons des exposés types qui
sont des enregistrements vidéos d’une dizaine à une
vingtaine de minutes portant sur des sujets fréquemment
enseignés lors de notre deuxième stage. Un des objectifs
de ces exposés est de montrer qu’on peut présenter les
mathématiques aux élèves en misant sur le sens, sur la
compréhension et de donner ainsi envie aux élèves de
faire des mathématiques. Ces enregistrements vidéo ont
été préparés par Mme Janvier, professeure maintenant à
la retraite.
GRMS ENVOL no 158 — janvier-février-mars 2012 29
L’exposé type, qui est à la source de la réflexion que je
présente ici, est celui sur la construction par pliage de
polygones réguliers ayant un nombre pair de côtés (par
exemple le carré, l’hexagone régulier, l’octogone régulier,
etc.) Les polygones sont étudiés au premier cycle du
secondaire, les élèves ont toutefois déjà été initiés à ce
sujet au primaire.
1. Étude des polygones dans les manuels
scolaires
Au troisième cycle du primaire, même si cette notion n’est
pas étudiée explicitement, les élèves sont capables de
nommer quelques polygones et ils savent aussi ce qu’est
un polygone régulier. On retrouve les polygones ailleurs
qu’en géométrie, par exemple, en arithmétique dans
l’étude des fractions où les élèves doivent représenter ou
reconnaître des fractions représentées dans des touts qui
sont des polygones réguliers.
Les manuels du primaire définissent les polygones
réguliers comme suit :
Un polygone régulier a tous ses côtés et tous ses
angles égaux.2
Un polygone est régulier si tous ses côtés
sont isométriques et si tous ses angles sont
isométriques3.
Dans le manuel Clicmaths, la construction de ces
polygones s’appuie sur un cercle (sur le résultat que tout
polygone régulier est inscriptible dans un cercle). La
technique consiste à séparer l’angle au centre en autant
d’angles que le polygone a de côtés.
1
Baccalauréat en enseignement secondaire en mathématiques à l’Université du Québec à Montréal.
2
Défi mathématique 3e cycle, volume 1, p.137.
3
Clicmaths, manuel 1 volume B, p. 235.

Clicmaths, 3e cycle du primaire, manuel de l’élève B, volume 1, p. 25
Les élèves construisent les polygones en utilisant le papier
crayon, les étapes sont données sans explications. Dans
les manuels du secondaire4, la construction présentée est
semblable. L’approche proposée par Mme Janvier est tout
autre. Dans les exposés types, les polygones réguliers
sont construits par pliage en utilisant une simple feuille
de papier, donc plus besoin d’instruments de mesure. De
plus, la construction par pliage s’appuie sur des propriétés
non utilisées dans l’approche des manuels comme les axes
de symétrie. Le pliage permet une étude en profondeur
des propriétés des polygones réguliers.
2. Construction par pliage de polygones
réguliers ayant un nombre PAIR de
côtés
La construction de polygones réguliers par pliage avec
un nombre pair de côtés est présentée dans trois exposés
types et repose sur certaines propriétés des polygones
réguliers :
- Tout polygone régulier est inscriptible dans un cercle.
- Les axes de symétrie rejoignent deux sommets
diamétralement opposés.
- Les angles sont isométriques, les côtés sont
isométriques.
- Tout polygone régulier est constitué d’autant de
triangles isocèles5 congrus qu’il y a de côtés, chacun de
ces triangles ayant comme sommet commun le centre
du polygone (qui correspond au centre du cercle inscrit),
les deux côtés isométriques étant des « rayons ».
4
Voir à titre d’exemple le manuel Perspective, manuel de l’élève B, volume 1, p.92.
5
Dans le cas de l’hexagone régulier, il s’agit de triangles équilatéraux.
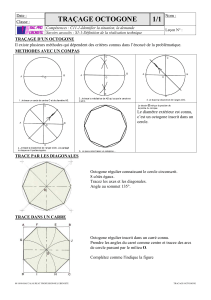
Figure 1
Note : Il est facile pour l’élève de trouver la mesure des angles et
de prouver que les triangles sont des triangles isocèles. Dans ce cas-
ci, nous avons un octogone régulier inscrit dans un cercle. Il suffit de
partager l’angle au centre de 360 degrés par le nombre de triangles
qui compose notre polygone. De plus, en traçant ces triangles, nous
distinguons aisément les axes de symétrie qui sont également les
diamètres du cercle dans lequel le polygone est inscrit.
Je vais présenter les grandes lignes qui guident la
construction par pliage d’un carré et d’un octogone
régulier. C’est à travers ces exposés types que ma réflexion
autour de la construction des polygones réguliers à un
nombre impair de côtés est née.
2.1 Construction par pliage d’un carré
Comme introduction, nous discutons brièvement de
l’épistémologie des noms des polygones réguliers jusqu’à
12 côtés (exemple : octogone : octo = 8, gone = angle). La
construction du carré se fait avec les élèves à l’aide d’une
simple feuille mobile. Nous nous appuyons sur le fait que
le carré a quatre côtés égaux et quatre angles de 90 degrés.
Dans l’exposé type, Mme Janvier présente deux façons de
construire un carré par pliage.
Méthode 1
Pour commencer la construction
d’un carré, il suffit de prendre la
largueur de notre feuille mobile,
ce qui constituera le premier côté
de notre carré.
GRMS
ENVOL no 158 — janvier-février-mars 2012
30

Il faut ensuite aller reporter ce
segment sur le côté adjacent
qui sera le deuxième côté du
carré. Nous nous retrouvons
avec deux des côtés de notre
carré et le premier angle de 90
degrés (les quatre coins de notre
feuille formant des angles de 90
degrés).
Si nous joignons les extrémités
de nos deux segments, nous
obtenons un triangle rectangle
isocèle. Nous savons que dans un
triangle rectangle isocèle, nous
avons un angle de 90 degrés et
deux angles de 45 degrés.
Nous pouvons remarquer que si
nous doublons nos deux angles
de 45 degrés, nous obtenons des
angles de 90 degrés. Donc, si nous
plions la feuille sur l’hypoténuse
de notre triangle rectangle, nous
obtenons ce résultat.
En reportant les segments, nous
obtenons notre carré avec quatre
angles de 90 degrés et quatre
côtés égaux.
Méthode 2
La deuxième approche s’appuie sur les axes de symétrie
du carré. Comme le même raisonnement sera utilisé pour
construire par pliage un octogone régulier, je ne reprendrai
pas ici cette construction.
2.2 Construction par pliage d’un octogone
régulier
La construction par pliage de l’octogone régulier s’appuie
sur le fait que les polygones réguliers sont inscriptibles
dans un cercle, les axes qui relient deux sommets
diamétralement opposés sont des axes de symétrie et les
segments qui relient chaque sommet de l’octogone au
centre du cercle inscrit sont en fait les rayons du cercle.
Il suffit donc de s’intéresser à la construction de la moitié
de l’octogone pour obtenir par pliage l’autre moitié de
l’octogone. Pour bien saisir le pliage, il faut avoir bien en
tête la figure 1.
On part avec une feuille mobile.
L’octogone a des axes de symé-
trie qui rejoignent deux som-
mets diamétralement opposés.
Construisons un de ces axes de
symétrie qui est également le
diamètre du cercle dans lequel
l’octogone est inscrit.
On plie la feuille en deux
parties égales. Une moitié du
polygone sera sur un côté du pli,
l’autre moitié de l’autre côté.
Sur chaque moitié, on aura 4
triangles isocèles isométriques.
Ces triangles auront un sommet
commun qui est le centre du
cercle inscrit.
Établissons le centre du cercle
inscrit. Il sera obtenu en pliant la
moitié de la feuille en deux (on
obtient également le centre de la
feuille). La feuille est maintenant
pliée en quatre, ce qui représente
le quart de l’octogone. Dans cette
partie seront représentés deux
triangles isocèles isométriques.
Il ne faut surtout pas perdre de
vue le centre du cercle inscrit sur
lequel s’appuie le pliage!
En pliant encore la feuille en
deux, on obtient l’angle au centre
d’un des triangles composant
l’octogone. Le sommet de cet
angle est le centre du cercle
inscrit. On vient ainsi de séparer
l’angle au centre en 8 angles
isométriques.
GRMS ENVOL no 158 — janvier-février-mars 2012 31

Il suffit maintenant de construire
les triangles isocèles. On prend
une longueur de côté arbitraire
que l’on reporte de l’autre côté.
Ce côté sera également le rayon
du cercle inscrit. On obtient
ainsi les deux côtés congrus des
triangles isocèles. On trace le
segment afin d’obtenir le triangle
et on coupe.
On a ainsi obtenu un des triangles
isocèles qui compose l’octogone
régulier. Il suffit de déplier la
feuille pour obtenir un octogone
régulier!
En construisant les polygones
réguliers par pliage, les élèves
travaillent directement sur les
propriétés des polygones, ils
les utilisent et en voient ainsi la
pertinence, l’utilité.
Comme prolongement, Mme Janvier souligne qu’il est
possible de tracer un carré en joignant tout simplement
deux sommets non consécutifs.
On remarque en procédant ainsi que si on part du carré,
il est possible de retrouver l’octogone. Les sommets de
l’octogone sont obtenus en traçant les médiatrices des
côtés du carré. Les sommets seront les intersections de ces
médiatrices avec le cercle inscrit. Le carré et l’octogone
sont ainsi liés. En procédant de la même façon, on pourrait
obtenir un polygone à 16 côtés, etc.
Conclusion
Dans cet article, nous avons vu les exposés types que
propose Mme Bernadette Janvier à l’UQAM dans les
cours de didactique de la mathématique. Dans la seconde
partie, qui paraîtra dans le prochain numéro, nous verrons
la construction par pliage de polygones réguliers ayant un
nombre IMPAIR de côtés.
Remerciements
Je tiens à remercier Mme Janvier d’avoir élaboré ces
exposés types sans lesquels cette réflexion n’aurait pu
avoir lieu. Merci également à Mireille Saboya, professeure,
pour ses commentaires lors des différentes versions de cet
article.
Références
M.E.L.S (Ministère de l’Éducation des loisirs et des sports),
Gouvernement du Québec (2003). Programme de
formation de l’école québécoise : Enseignement
secondaire, premier cycle. Québec : Ministère de
l’Éducation.
Défi mathématique, 3e cycle, volume 1 (2005). Lyons, M.
et Lyons, R. Chenelière Éducation.
Clicmaths, 3e cycle, manuel 1, volume B (2003). Guay,
S., Hame, J.C. et Lemay, S. Éditions Grand Duc.
Perspective, 1 cycle, manuel B, volume 1 (2006). Guay,
S., Hamel. J.C. et Lemay, S. Éditions Grand Duc.
GRMS
ENVOL no 158 — janvier-février-mars 2012
32
Nous vous invitons à aller sur notre site web :
www.grms.qc.ca
pour y consulter le document sur notre proposition
des statuts et règlements révisés.
Bonne lecture!
INVITATION