Chapitre 6 : Trigonométrie

Chapitre 6 : Trigonométrie
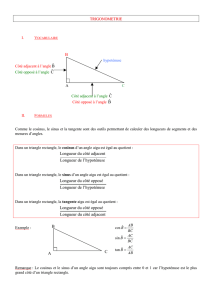
I. Angles et triangles rectangles
Définitions : Dans un triangle rectangle,
- Le cosinus d'un angle aigu est égal au quotient du côté adjacent à cet angle par l'hypoténuse ;
- Le sinus d'un angle aigu est égal au quotient du côté opposé à cet angle par l'hypoténuse ;
- La tangente d'un angle aigu est égal au quotient du côté opposé par le côté adjacent à cet
angle.
En résumé, on a : moyen mnémotechnique
cos angle=côté adjacent
hypoténuse
CAH
sin angle=côté opposé
hypoténuse
SOH
tan angle=côté opposé
côté adjacent
TOA
Exemples :
Dans le triangle RST rectangle en R, on a :
cos RST =RS
ST
sin RST =RT
ST
tan RST =RT
RS
Ex 6 et 7 p 237 / Ex 29 à 31 p 240
hypoténuse
Coté adjacent à x
Coté opposé à x
x

II. Calculer une longueur
Méthode :
- On précise quel est le triangle rectangle utilisé ;
- On repère dans le triangle, l'angle connu ; le côté connu ; puis la longueur recherchée.
- En fonction de ces 3 « données », on détermine la formule à utiliser ;
- On écrit la formule avec les lettres (du triangle), puis on remplace par les valeurs connues.
- Grâce à un produit en croix (et en rajoutant 1), on trouve la valeur du côté cherché.
Exemples :
–ABC est un triangle rectangle en B tel que AB = 4 cm ;
ACB=42°
.
Calculer AC.
« Je connais l'angle
ACB
et son côté opposé AB , je cherche l'hypoténuse AC.
J'utilise donc le sinus. »
sin ACB=AB
AC
sin42
1=4 AC
donc
AC=4×1
sin 42≈5,98 cm
–Le triangle MNP rectangle en P est tel que MN = 6,5 cm et
MNP=28°
Calculer NP.
« Je connais l'angle
MNP
et l'hypoténuse MN , je cherche son côté adjacent NP.
J'utilise donc le cosinus. »
cos MNP=NP
MN
cos28
1=NP 6,5
donc
NP=6,5×cos 28≈5,74 cm
Ex 11 à 17 p 238
III. Calculer un angle
Méthode :
- On précise quel est le triangle rectangle utilisé.
- On repère dans le triangle, l'angle recherché et les deux côtés connus.
- En fonction de ces 3 « données », on utilise le cosinus, le sinus ou la tangente.
- On écrit la formule avec les lettres (du triangle); puis on remplace par les valeurs connues.
- Grâce aux touches
cos–1
,
sin–1
et
tan–1
, on calcule la valeur de l'angle
(en général au degré près).
Exemples :
–Le triangle EFG est rectangle en E tel que EF = 5 cm et FG = 7 cm.
Calculer
EFG
au degré près.
« Je cherche l'angle
EFG
, je connais son côté adjacent et l'hypoténuse.
J'utilise donc le cosinus. »
cos EFG =EF
FG
cos EFG =5
7
donc,
EFG≈44 °
« Sur la calculatrice, on tapé
cos–1
5
7
. »

–Le triangle XYZ est rectangle en Y tel que XY = 3 cm et YZ = 4,5 cm.
Calculer
XZY
au degré près.
« je cherche l'angle
XZY
, je connais son côté adjacent et son côté opposé.
J'utilise la tangente. »
tan XZY =YZ
XY
tan XZY =4,5
3
donc,
XZY ≈56°
« Sur la calculatrice, on a tapé
tan–1
4,5
3
. »
Ex 18 à 25 p 239
Exercices type brevet : Ex 52 à 56 p 242
+ Mathenpoche : Chapitre G2