DISTANCE, TANGENTE ET BISSECTRICE

[1]
C. Lainé
DISTANCE, TANGENTE
ET BISSECTRICE
1. Distance d’un point à une droite
La distance AH est la distance
entre le point A et la droite
(
)
d
.
Les distances séparant le point
A de n’importe quel autre point
de la droite
(
)
d
(par exemple,
comme les distances AB, AC
ou AD) sont toutes supérieures
à la distance
AH.
La distance d’un point A à une droite
(
)
d
est la distance la plus courte qui
sépare ce point A des points de la droite
(
)
d
.
La distance d’un point A à une droite
(
)
d
est la distance AH, où H est le point
d’intersection de
(
)
d
avec la perpendiculaire à
(
)
d
passant par A.
Objectifs :
• Savoir que le point d’une droite le plus proche d’un point donné est le
pied de la perpendiculaire menée du point à la droite.
• Construire la tangente à un cercle en l’un de ses points.
• Connaître et utiliser la définition de la bissectrice .
• Utiliser différentes méthodes pour tracer :
- la médiatrice d’un segment ;
- la bissectrice d’un angle.
• Caractériser les points de la bissectrice d’un angle donnée par la
propriété d’équidistance aux deux côtés de l’angle.
• Construire le cercle inscrit dans un triangle.

[2]
C. Lainé
2. Tangente à un cercle
La distance OA est la distance entre le point
O et la droite
(
)
d
; alors la droite
(
)
T
est la
tangente au cercle
(
)
c
au point A.
Cette tangente est la droite perpendiculaire
en A au rayon
[
]
OA
.
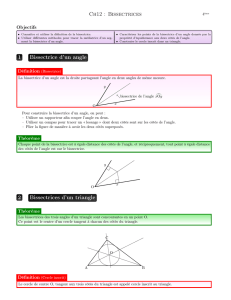
3. Bissectrice d’un angle
La tangente en un point A à un cercle
(
)
c
de centre O est la droite située à une
distance OA du centre du cercle, et qui passe par A.
La tangente en un point A à un cercle
(
)
c
de centre O est la droite
perpendiculaire en A au rayon
[
]
OA
.
La bissectrice d’un angle est la demi-droite qui a pour origine le sommet de
l’angle, et qui partage l’angle en deux angles adjacents de même mesure.
bissectrice de l’angle
BAC
La bissectrice d’un angle est l’axe de symétrie de cet angle.

[3]
C. Lainé
Méthodes de construction de la bissectrice d’un angle donné :
•
Avec un rapporteur
:
•
Avec un
compas
:

[4]
C. Lainé
4. Cercle inscrit dans un triangle
Démonstration :
• Le point O est situé sur la bissectrice
de l’angle
BAC
; le point O est alors
situé à égale distance des côtés
[
]
AB
et
[
]
AC
. Par suite, on obtient
OE OD
=
.
• Le point O est situé sur la bissectrice
de l’angle
ABC
; le point O est alors
situé à égale distance des côtés
[
]
BA
et
[
]
BC
. Par suite, on obtient
OE OF
=
.
• On en déduit que
OE OF OD
= =
, et
donc que les points D, E et F sont sur
un cercle c de centre O.
Remarque : Les trois côtés d'un triangle sont tangents au cercle inscrit dans ce triangle.
Propriété
:
• Si un point
est situé à la même distance des côtés d'un angle
alors il appartient à la bissectrice de cet angle.
• Réciproquement, si un point appartient à la bissectrice d'un angle alors il
est situé à la même distance des côtés de cet angle.
Propriété
:
Les bissectrices des angles d’un triangle se croisent en un même
point ; on dit qu’elles sont concourantes.
Le point commun à ces trois bissectrices est le centre du cercle inscrit dans ce
triangle : chacun des côtés du triangle est tangent à ce cercle.

[5]
C. Lainé
Résumé
Médiatrices Bissectrices
Définitions
La médiatrice d’un segment est la
droite perpendiculaire à ce segment
et qui passe par son milieu.
La bissectrice d’un angle est la
droite qui le partage en deux angles
adjacents de même mesure.
Figures
Points de
concours
Centre du cercle circonscrit
au triangle
Centre du cercle inscrit
dans le triangle
Propriétés
OA OB OC
= =
Le point de concours des médiatrices est
équidistant des trois sommets du triangle.
OE OF OD
= =
Le point de concours des bissectrices est
équidistant des trois côtés du triangle.