2 cinematique du point repare

Mécanique du solide I. AL KORACHI
Chapitre 1 : Cinématique du point Ecole des Hautes Etudes d’Ingénierie Oujda
1
Chapitre 1 : Cinématique du point
1-Repérage du mouvement d’un point M
 :
Pour décrire correctement le mouvement, on considère un point O fixe appelé aussi point de
référence du mouvdu mouvement, il sert tout simplement à relativiser le
mouvement.
Pour représenter les grandeurs vectorielles cinématique ou dynamique (La position, la vitesse,
la force orthonormée directe 
2-Définition d’un repère orthonormé direct
Le centre O est le point de référence du mouvement et   est une base orthonormée
directe, alors  est un repère orthonormé direct.
.
Propriétés :
est un repère orthonormé direct cartésien
 sont les axes du repère :  ,  es
ordonnées du repère et  des altitudes du repère.
3-Définition d’un référentiel orthonormé direct
Le centre O est le point de référence du mouvement,   est une base orthonormée directe
est un référentiel orthonormé, direct et cartésien.
Propriétés :
Le référentiel orthonormé direct    :
 est fixe ou en mouvement rectiligne uniforme par rapport un autre référentiel
orthonormé direct fixe.
Mouvement rectiligne : Mouvement selon une droite.
Mouvement uniforme : Module de vitesse constant.
4-Vecteur-position 
Soit M un point en Mouvement,
Soit  un référentiel orthonormé, direct, cartésien et Galiléen.
La trajectoire du mouvement du point M est la courbe formée par les points parcourus par M.
M
M
x
y
z
y
y
y
y

Mécanique du solide I. AL KORACHI
Chapitre 1 : Cinématique du point Ecole des Hautes Etudes d’Ingénierie Oujda
2
Le vecteur 
 est le vecteur-position du point M
Le vecteur vecteur-position, détermine la position du point M.
 : est le vecteur déplacement du point M.
 : Le vecteur déplacement infinitésimal du point M.
5- Vecteur-vitesse 
La dérivée du vecteur-position du point M par rapport au temps  est égale au vecteur-
vitesse 
 du point M :
La norme du vecteur-vitesse 
 du point M mesure la rapidité du point M.
Le vecteur-vitesse 
 est toujours tangentiel à la trajectoire dirigé vers le sens du
mouvement. 
Vecteur unitaire tangentiel à la trajectoire dirigé vers le sens du mouvement. (Regarder la
figure en haut)
6-Vecteur-accélération 
:
La dérivée du vecteur-vitesse 
de M par rapport au temps  est égale au vecteur-
accélération 
de M :
x
y
z
y
y
y
y
Trajectoire

Mécanique du solide I. AL KORACHI
Chapitre 1 : Cinématique du point Ecole des Hautes Etudes d’Ingénierie Oujda
3
: Vecteur unitaire normal à la trajectoire (normal à  ) dirigé vers le centre de courbure.
R : Rayon de courbure.
2)
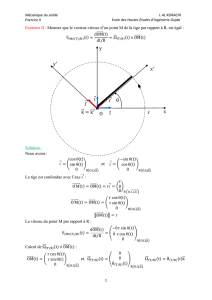
7-Mouvement de rotation
Soient  un repère orthonormé direct et        
 qui porte  et passe par O.
 un repère orthonormé, direct lié à la tige et 
Vitesse de rotation ou vitesse angulaire
de la tige entre deux points A et B est la distance parcourue par ce mobile M entre A et B
(Arc 
 ) divisée par le temps mis pour parcourir cette distance   :
Le module de la vitesse instantanée (vitesse scalaire instantanée) du point M :
.
=
=
=

Mécanique du solide I. AL KORACHI
Chapitre 1 : Cinématique du point Ecole des Hautes Etudes d’Ingénierie Oujda
4
La vitesse de rotation ou la vitesse angulaire de la tige est égale :
 qui porte  et passe par O.
: V qui porte  et
passe par O.
Tous les points de la tige ont la même vitesse de rotation ,  pour cela que
est appelée la vitesse de rotation de la tige par rapport à R.
de la tige :
Quelque soit le point M qui appartient à la tige, sa vitesse scalaire instantanée est égale à la
distance r qui sépare ce point M du centre O de rotation, multipliée par la vitesse de rotation
de la tige : 
Démonstration :
Le module de la vitesse instantanée (vitesse scalaire instantanée) du point M de la tige, situé à
Vecteur-vitesse instantané de rotation de la tige :
       -       
droite qui porte le vecteur  et qui passe nécessairement par le centre O et  est la
composante du vecteur-vitesse de rotation instantanée, finalement, Le vecteur-vitesse
instantané de rotation de la tige
qui porte par O et porte  ) sont au repos, c'est-à-dire leurs vitesses sont nulles.
Relation entre le vecteur-vitesse instantané          -vitesse
instantanée de rotation de la tige :
Le vecteur- tige par rapport à R, est égal : Exercice 2