DEVOIR MAISON N°1

Mathématiques – classe de 5ème
DEVOIR MAISON n°3
A rendre avant le lundi 11 janvier 2016
Construction géométrique (Sujet A)
inspiré de La géométrie pour le plaisir – J. et L. DENIERE – Editions DENIERE
Critères d'évaluation
(vert – orange - rouge)
Auto-
évaluation
Evaluation du
professeur
Soin et précision de la construction
Réaliser une figure à partir d'un programme de
construction
Utilisation du rapporteur pour tracer un angle.
Objectif : Suivre le programme de
construction pour réaliser avec soin
et précision cette figure sur une
feuille non quadrillée et la colorier
aux feutres.
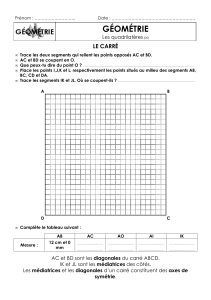
Trace deux segments [AB] et [CD] de 18
cm de longueur et se coupant
perpendiculairement en leur milieu O.
Place sur ces segments les points I, J,
K, L situés à 3 cm du point O.
Trace les angles xID et yID de 35°
chacun, puis les angles xIz et yIt de 25°
chacun.
Gradue le segment [ID] tous les centimètres et, à partir de chaque point, trace les
perpendiculaires à [lx) et à [ly). Refais les mêmes constructions à partir de [KA],
[LC] et [BJ].
Les demi-droites [Kr) et [Iz) se coupent en M.
Joins les points N et P (voir sur la figure la place de ces points).
Trace ensuite les segments [NM], [MP] et [KI].
Refais les constructions identiques à partir des autres points.
Le défi du mois : les diagonales
Un polygone à 4 côtés est un quadrilatère, il possède 2 diagonales.
Un polygone à 5 cotés est un pentagone, il possède 5 diagonales.
Combien un dodécagone possède t-il de diagonales ?
En bonus : Combien un chiliagone possède t-il de diagonales ?

Mathématiques – classe de 5ème
DEVOIR MAISON n°3
A rendre avant le lundi 11 janvier 2016
Construction géométrique (Sujet B)
inspiré de La géométrie pour le plaisir – J. et L. DENIERE – Editions DENIERE
Critères d'évaluation
(vert – orange - rouge)
Auto-
évaluation
Evaluation du
professeur
Soin et précision de la construction
Réaliser une figure à partir d'un programme de
construction
Utilisation du rapporteur pour tracer un angle.
Objectif : Suivre le programme de
construction pour réaliser avec soin
et précision cette figure sur une
feuille non quadrillée et la colorier
aux feutres.
Trace deux cercles (C) et (C') de centre
O et de rayons respectifs 8 cm et 9 cm.
Sur le cercle (C), place un point A et
reporte 6 fois la longueur du rayon (8
cm). On obtient les points A, B, C, D, E,
F. Trace les cordes [BC], [DE] et [FA].
Il faudra refaire 3 fois chacune des
constructions expliquées ci-
dessous :
Trace la bissectrice de l'angle AOB, elle coupe le cercle (C') en G.
Trace un triangle isocèle OAH de base [OA] et dont l'un des côtés est porté par
[OG]. Pour cela, trace la médiatrice de [OA] qui coupe [OG] en H. Fais la même
construction à partir de [OF].
Trace le segment [HB] et refais les mêmes constructions.
Trace ensuite tous les segments parallèles à ceux tracés à une distance de 1 cm.
Soit K le milieu de [IJ]. (voir sur le dessin où placer I et J).
Trace [OK] et prolonge. Soit L l'intersection de (OK) avec le cercle (C).
Trace les segments [KM], [ KN] et [ KP] (voir sur le dessin où placer les points M, N,
P).
Trace une partie des segments [LM] et [LP]. Soit S le milieu de [AH] et T celui de
[BH]. Tracez les segments [GS] et [GT].
Le défi du mois : les diagonales
Un polygone à 4 côtés est un quadrilatère, il possède 2 diagonales.
Un polygone à 5 cotés est un pentagone, il possède 5 diagonales.
Combien un dodécagone possède t-il de diagonales ?
En bonus : Combien un chiliagone possède t-il de diagonales ?

Mathématiques – classe de 5ème
DEVOIR MAISON n°3
A rendre avant le lundi 11 janvier 2016
Construction géométrique (Sujet C)
Extrait de l'IREM de Lille – Auteur : Stéphane Vanreust
Critères d'évaluation
(vert – orange - rouge)
Auto-
évaluation
Evaluation du
professeur
Soin et précision de la construction
Réaliser une figure à partir d'un programme de
construction
Utilisation du rapporteur pour tracer un angle.
Objectif : Suivre le programme de construction pour réaliser avec soin et
précision cette figure sur une feuille non quadrillée et la colorier aux
feutres.
Le Zellige :
Un Zellige est un petit élément d'une marqueterie de céramique émaillée servant au
décor monumental dans l'art maghrébin.
1) Tracer, sur une feuille blanche, deux cercles concentriques de centre O et de
rayons 5 cm et 10 cm.
2) Sur le petit cercle, placer un point A, reporter le rayon de 5 cm à partir de A :
vous obtenez les points B, C, D, E et F.
3) Tracer le triangle OAB. Puis tracer les médianes du triangle OAB pour obtenir I,
leur point d'intersection, qui est le centre de gravité du triangle.
4) Tracer [IA], [IB], [IO].
5) Prolonger [OI). Soit L son intersection avec le grand cercle.
6) Prolonger [OB). Soit M son intersection avec le grand cercle.
7) Prolonger [OA). Soit N le point d'intersection avec le grand cercle.
8) Tracer le triangle ABL. Placer J son centre de gravité. Tracer [JA], [JB], [JL].
9) Tracer le triangle BLM . Placer K son centre de gravité. Tracer [KB], [KL], [KM].
10) Tracer le triangle ALN . Placer H son centre de gravité. Tracer[HA], [HL], [HN].
11) Procéder 5 fois de même à partir des triangles OBC , OCD, ODE, OEF et OFA
12) Colorier l'ensemble de 3 couleurs différentes.
Le défi du mois : les diagonales
Un polygone à 4 côtés est un quadrilatère, il possède 2 diagonales.
Un polygone à 5 cotés est un pentagone, il possède 5 diagonales
Combien un dodécagone possède t-il de diagonales ?
En bonus : Combien un chiliagone possède t-il de diagonales ?