maths-5e-paques-2015-corrige.

Corrigé de la fiche de travail Avril 2015
Classe de 5e
Exercice 1 
1) a) + 4,59 5 c) – 2,7 - 3
b) – 0,41 0 d) 0,33 0
2) - 2 + (- 6) = - 8 2 - 6 = - 4
- 2 - 1 = - 3 5 + (- 8) = - 3
- 7 + 4 + 2 = - 1 - 10 - (- 5) = - 5
3) a)
b)
Exercice 2
• A’(+2,5) et B’(-5,6)
• AB = ?
AB = Abs B – Abs A
= 5,6 – (-2,5)
= 5,6 + 2,5
= 8,1
• A’B’= ?
A’B’ = Abs A’ – Abs B’
= 2,5 – (-5,6)
= 2,5 + 5,6
= 8,1
• Donc AB = A’B’ = 8,1
Exercice 3
• B (-5 ; -3)
• C (-1 ; 4)
• D (1 ; 4)
• E (-4 ; -1)
• F (5 ; 3)
F serait le symétrique de A par rapport à
l’axe des ordonnées
et le symétrique de B par rapport à
l’origine.
Exercice 4
2) Le quadrilatère ABEM a :
C milieu de [AE] (p.h)
C milieu de [BM] car M symétrique de B par rapport à C
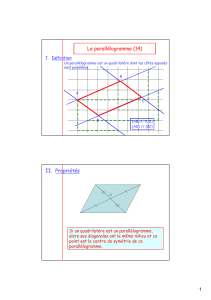
Or si un quadrilatère a ses diagonales qui se coupent en leur milieu alors c’est un parallélogramme
Donc ABEM est un parallélogramme.
3) Le quadrilatère ACMD a :
BC=AD et (BC) parallèles à (AD) car les côtés opposés du parallélogramme ABCD sont parallèles et de
même longueur.
A = - 2,2
B = - 2,7
D = 2
E = 0
F = 2
G = - 4
H = 21
I = 7,2
J = 8,8
10,1
10,2
-0,1
7,2
3
-3,1
6,3
0,9
2,1
-5,2

BC=CM car C milieu de [BM] alors CM=AD et (CM) parallèles à (AD)
Or si un quadrilatère a 2 côtés opposés parallèles et de même longueur alors c’est un parallélogramme.
Donc ACMD est un parallélogramme.
4) ABCD est un parallélogramme donc
oooo CBADAB 13050180
ˆ
180
ˆ=−=−=
car les angles consécutifs
d’un parallélogramme sont supplémentaires.
Alors
o
CABDABCAD 70
ˆˆˆ =−=
ACMD est un parallélogramme donc
CADCMD ˆ
ˆ=
car les angles opposés d’un parallélogramme sont de
même mesure.
Alors
=CMD ˆ
o
70
Exercice 5
1. Le quadrilatère ABCD a
AD=BC (p.h)
(xy) et (BC) sont parallèles, AЄ (xy) et DЄ (xy) donc (AD) et (BC) parallèles.
Or si un quadrilatère a 2 côtés opposés parallèles et de même longueur alors c'est un parallélogramme.
Donc ABCD est un parallélogramme par suite (AB) parallèle à (CD) et AB=CD car dans un
parallélogramme les côtés opposés sont parallèles et de même longueur.
2. Les 2 droites (AB) et (DC) sont coupées par la sécante commune (xy) en A et D respectivement formant
deux angles correspondants
BAxˆ
et
CDA ˆ
.
De plus (AB) parallèle à (CD) (d.d)
Donc
BAxˆ
=
CDA ˆ
.
3. ABCD parallélogramme donc ses angles consécutifs sont supplémentaires
alors
CDA ˆ
=
oo DCB 75
ˆ
180 =−
or
BAxˆ
=
CDA ˆ
donc
BAxˆ
=
o
75
.
Exercice 6
1) Les droites ( CH) et (CK) semblent être perpendiculaires.
2) On a : - J milieu de [BK] ( car K symétrique de B par rapport à J)
- J milieu de [AC]
Or : si un quadrilatère a les diagonales qui se coupent en leur milieu alors c’est un parallélogramme.
alors : ABCK parallélogramme
donc (AB) (CK) car dans un parallélogramme les cotés opposés sont deux à deux parallèles.
de plus (HC)  (AB) donc (CH)  (CK)
Exercice 7
a) M milieu de [AC] et M milieu de [IP] car P symétrique de I par rapport à M
Alors IAPC est un parallélogramme car……………….
b) I milieu de [AB] alors IA = IB et I; A et B sont alignés
AICP parallélogramme alors AI = PC et (AI) parallèle à (PC)
Donc IB = PC et (IB) parallèle à (PC)
Alors IPCB est un parallélogramme car…………………………..
c) IPCB est un parallélogramme alors IP = BC et (IP) parallèle à (BC)
or M milieu de [IP] alors (IM) parallèle à (BC) et IM= BC/2
d) AIP = 50® angles correspondants
IPC = 50® angles opposes du parallélogramme IPCB
PCB = 130® angles supplémentaires
e) IC =AP et IC = PE (IC) parallèle à (AP) et (IC) parallèle à (PE)
alors AP = PE et A ; P et E alignés donc P est le milieu de [AE].