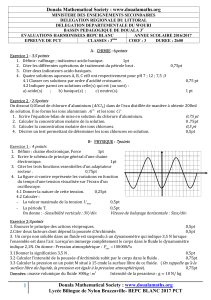
On fait subir à une mole d'eau la transformation EFGHIJE... Les volumes molaires de l'eau liquide respectivement aux

Contrôle Rattrapage – Thermodynamique 2
SMP – S3 – Durée 1h30 - 2012
Exercice 1 : Chaleur latente de vaporisation en fonction de la température (10.5pts)
On fait subir à une mole d'eau la transformation EFGHIJE (figure ci-dessous).
Les volumes molaires de l'eau liquide respectivement aux
températures
T
et
'
T
sont notés
f
V et
'
f
V De même on
note
g
V et
'
g
V les volumes molaires de la vapeur d'eau
aux températures
T
et
'
T
. On négligera les volumes
molaires du liquide face aux volumes molaires de la
vapeur. Les capacités calorifiques molaires
f
C et
g
C
respectivement des phases liquide et vapeur, sont
considérées comme indépendantes de la température.
La vapeur d'eau est assimilée à un gaz parfait même à l’état de saturation et
gf
CC > .
1. Représenter le cycle étudié sur le diagramme en coordonnées T-v.
2. On appelle
L
et
'
L
les chaleurs molaires de vaporisation respectivement aux températures
T
et
'
T
. Donner et indiquer le signe des travaux échangés
EF
W ,
FG
W ,
GH
W ,
HI
W ,
IJ
W et
JE
W .
Donner et indiquer le signe des chaleurs échangées
EF
Q ,
FG
Q ,
GH
Q ,
HI
Q ,
IJ
Q et
JE
Q .
3. Utiliser le premier principe de la thermodynamique et déterminer l'expression de la différence
'
L
L
−
en fonction de
f
C,
g
C ,
T
et
'
T
. En déduire que la chaleur latente peut s'écrire sous
la forme ATLL
0
−= où
0
L et
A
sont deux constantes positives à déterminer .
4. Tracer l'allure de la courbe de variation de
L
en fonction de
T
.
5. Que peut-on dire de la température à laquelle
L
=0.
Exercice 2 : Turbine Prendre : c
p
(air) = 1000 J/kg/K, R = 8,314 J/mol/K, M
air
= 29g (3.5pts)
De l’air (gaz parfait, c
p
=1kJ/kg/K ) se détend dans les aubages d'une turbine. L'enthalpie massique
à l’entrée est
1
h=865,3kJ/kg et la vitesse étant
1
c=70m/s. L'enthalpie massique à la sortie est
2
h=332kJ/kg et la vitesse à la sortie est
2
c=100m/s. Le débit massique est de s/kg10m
=
&.
1/ En supposant le processus adiabatique, calculer la puissance
t
W
&
développée par la turbine.
2/ La température d’entrée vaut C627T
1
°= . Calculer la température
2
T à la sortie.
3/ Dans la réalité le processus n’est pas adiabatique et la turbine fournit une puissance
kW4620W
'
t
=
&
. Calculer la chaleur échangée
't
Q et le rendement
s
η de la turbine.
Exercice 3 : Transformations adiabatiques réversible et irréversible (8pts)
Un gaz parfait (de constantes R et
γ
) subit une compression adiabatique de l’état (
1
1
T,P ) à
l’état (
2
P ). Exprimer toutes les réponses en fonction de ces données.
*
a) Compression réversible : calculer
2
T ,
2
V , le travail
12
W échangé et l’entropie
c
S créée.
b) Compression irréversible : calculer
'
2
T ,
'
2
V , le travail
'
12
W échangé et l’entropie
'c
S créée.
-------------------------------------------------------------------------------

Indication de solution aux exercices du contrôle rattrapage
SMP S3 Automne 2012
Exercice 1 : Chaleur latente de vaporisation en fonction de la température (10pts)
2/ Calcul des travaux et des chaleurs échangés. Noter que 0,5pt pour l’expression et le signe
(c'est-à-dire 0,25pt pour l’expression et 0,25pt pour le signe).
Transformation isotherme EF :
'
P
P
ln'RTW
EF
−= >0 (0.5pt)
'
P
P
ln'RTQ
EF
= <0(0.5pt)
Où
E
'
g
EF
V
V
ln'RTW −=
E
'
g
EF
V
V
ln'RTQ =
Changement d'état FG : )'V'V('PW
gfFG
−−= >0(0.5pt)
'
gFG
V'PW ≈ 'LQ
FG
−= <0(0.5pt)
Transformation isobare GH : 0W
GH
≈ (0.5pt) )'TT(CQ
fGH
−= <0(0.5pt)
Transformation isotherme HI : 0W
HI
= (0.5pt) 0Q
HI
= (0.5pt)
Changement d'état I-->J : )VV(PW
fgIJ
−−= <0(0.5pt)
gIJ
PVW −≈ LQ
IJ
= >0(0.5pt)
Transformation isobare J-->E : )VV(PW
gEJE
−−= <0(0.5pt) )T'T(CQ
gJE
−= >0(0.5pt)
3/ Le premier principe de la thermodynamique, donne 0)QW(U
iicycle
=+Σ=∆ (0.5pt).
En utilisant l’équation des gaz parfaits et pour 1 mole, on obtient )'TT)(CC('LL
gf
−−−=− (0.5pt).
c'est-à-dire aTLL
0
−= avec 'T)CC('LL
gf0
−+= (0.5pt) et
gf
CCa −= (0.5pt).
4/ D’après la question 3/ L(T) est approximé par une relation linéaire à pente négative, d’où la courbe :
5/ Quand
C
TT → ,
fg
VV → et 0L
→
. Il s’agit donc de la température critique Tc (Liq/Vap) (0.5pt)
voir la courbe de la figure sur le texte de l’exercice.

Exercice 2 : Turbine (4pts)
1/ Le premier principe de la thermodynamique des systèmes ouverts :
t
2
1
2
2
12
W)
2
cc
hh(m &
&=
−
+− (1pt), ce qui donne par A.N. kW5,5307W
t
−=
&
(0.5pt)
2/ )TT(chh
12p12
−=−
⇒
1
p
12
2
T
chh
T+
−
=
(0.5pt) donne K7,366T
2
= (0.5pt).
3/ On a :
't '
t
2
1
2
2
12
QW)
2
cc
hh(m &
&
&+=
−
+− (0.5pt), d’où m/)WW(Q
'
tt
't
&
&&
−= (0.5pt). Par application
numérique, on obtient : kg/kJ75,6875,530462Q
't
−=−= (0.5pt).
Exercice 3 : Transformations adiabatiques réversible et irréversible (6pts)
a/ Transformation est adiabatique réversible : Gaz parfait :
1
1
1
RTVP = donnent :
γ
−γ
=
1
1
2
12
P
P
TT (0,5pt) et
γ
=
1
2
1
1
1
2
P
P
P
RT
V (0,5pt),
)1
P
P
(
1
RT
)TT(cW
1
1
21
12v12
−
−γ
=−=
γ
−γ
(0.5pt) et S
c
= 0(0.5pt).
b) Transformation est adiabatique irréversible : )TT(
1
R
W
1
'
2
'
12
−
−γ
= et )VV(PW
1
'
2
2
'
12
−−= et
puisque
'
2
2
'
2
VPRT = on obtient
121
'
2
VPT
1
R
1
R
T+
−γ
=
−γ
γ
- Calcul de
'
2
T : ))1(
P
P
1(
T
1
P
T
P
T
T
1
21
1
1
2
1
'
2
−γ+
γ
=
γ
−γ
+
γ
= donne ))1(
P
P
1(
T
T
1
21
'
2
−γ+
γ
= (1pt)
- Calcul de
'
2
V : )1(
P
P
1
P
RT
Vou
R1 P
RT
P
T
P
R
V
1
2
2
1
'
2
1
1
2
1
2
'
2
−γ+
γ
=
γ−γ
+
γ
= (1pt)
donne )1(
P
P
1
P
RT
V
1
2
2
1
'
2
−γ+
γ
=
- Calcul de
'
12
W : )1
P
P
(
RT
)T
R1
VP
T
(
1
R
W
1
21
112
1
'
12
−
γ
=−
γ−γ
+
γ−γ
= donne :
)1
P
P
(
RT
W
1
21
'
12
−
γ
= (1pt)
En utilisant l’autre expression ]V))1(
P
P
1(
P
RT
[PW
1
1
2
2
1
2
'
12
−−γ+
γ
−= on arrive au même résultat :

]
P
P
1[
RT
W
1
21
'
12
−
γ
−=
- Calcul de
'c
S : Il est plus simple d’utiliser la pression,
2
1
1
'
2
P
2
1
'c
P
P
lnR
T
T
lnc
T
Q
SS +=
δ
=∆=
∫
(0.5pt),
ce qui donne
2
1
1
2
'c
P
P
lnR))1(
P
P
1(
1
ln
1
R
S+
−γ+
γ−γγ
= (0.5pt)
Si non on utilisera le volume et on aura :
1
'
2
1
'
2
V
2
1
'c
V
V
lnR
T
T
lnc
T
Q
SS +=
δ
=∆=
∫
qui donne :
−γ+
γ
+
−γ+
γ−γ
=)1(
P
P
1
P
P
lnR))1(
P
P
1(
1
ln
1
R
S
1
2
2
1
1
2
'c
, que l’on peut ramener à l’expression ci-
dessus.