télécharger le PDF

c
Éditions H&K Publié dans les Annales des Concours 1/18
ENAC Physique toutes filières 2003 — Corrigé
Ce corrigé est proposé par Jean-Julien Fleck (ENS Ulm) ; il a été relu par
Aurélien Fraisse (ENS Cachan) et Arnaud Gossart (Professeur en CPGE).
Ce sujet est divisé en cinq parties totalement indépendantes, qui abordent une
grande part du programme de première année :
•La première partie est consacrée à l’électrocinétique. On y étudie un dispositif
de mesure de fréquence par équilibrage d’un pont d’impédances.
•La deuxième traite d’électrostatique et de magnétostatique par l’étude des in-
teractions de deux fils infinis chargés ou parcourus par des courants.
•La troisième présente un filtre linéaire à amplificateur opérationnel.
•La quatrième étudie la cinématique de la chute d’une barre, connaissant le
mouvement de ses extrémités. Il s’agit principalement de géométrie dans le
plan et dans l’espace.
•La cinquième partie, quant à elle, traite d’optique géométrique via un système
de trois lentilles qui généralise le principe de la lunette de Galilée.
Ce sujet est plutôt facile puisque constitué d’une juxtaposition de cinq exercices de
type « colles » ne comportant généralement qu’une seule question un peu calculatoire.
Chaque partie permet de vérifier que l’on a bien compris les chapitres du programme
correspondants par des questions d’application du cours quasi-directes.
Téléchargé gratuitement sur www.Doc-Solus.fr .

c
Éditions H&K Publié dans les Annales des Concours 2/18
Indications
Électrocinétique
1 Faire un schéma faisant apparaître très clairement les différentes mailles du circuit,
puis exprimer VCet VDen fonction de VBet E grâce à des diviseurs de tension.
Électrostatique et magnétostatique
5 Utiliser les symétries du système pour appliquer le théorème de Gauss.
7 Différentier la relation tan θ=HM
dpour obtenir dℓen fonction de dθ.
9 Utiliser les symétries du système pour appliquer le théorème d’Ampère.
11 Projeter −→ eϕsur −→ exet −→ ey.
Filtre linéaire à amplificateur opérationnel
13 Utiliser les deux propriétés d’un amplificateur opérationnel en régime linéaire
pour éliminer VAet VBde la relation de Millman en B.
Cinématique
19 Le théorème d’Al Kashi s’écrit, pour un triangle ABC quelconque,
AC2= AB2+ BC2−AB ·BC cos
[
ABC
20 Utiliser le fait que ρest la projection de du segment [AB] sur le plan (xOy).
21 La projection de J sur le plan (xOy)est le milieu du segment [OB].
23 Une valeur moyenne sur un temps T se calcule par la formule
hfi=1
TZT
0
f(t) dt
Optique géométrique
27 La lentille L2ne joue aucun rôle pour des rayons en provenance de l’infini.
28 Utiliser la formule de conjuguaison de Newton
FA ×F′A′=−f′2
30 Exprimer le grandissement γen fonction de pou p′uniquement à l’aide de la
formule de Descartes.
Téléchargé gratuitement sur www.Doc-Solus.fr .

c
Éditions H&K Publié dans les Annales des Concours 3/18
I. Électrocinétique
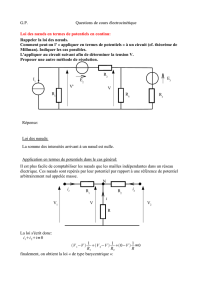
1Trouver la force électromotrice de Thévenin re-
vient à calculer la différence de potentiel entre les
bornes C et D à vide (on parle de tension de circuit
ouvert). La difficulté principale est bien souvent de
redessiner le circuit pour bien identifier les quantités
à calculer. Dans cette optique, le circuit se réarrange
comme sur le schéma ci-contre.
On reconnaît ainsi deux diviseurs de tension :
VD−VB=R
R + nRE
VC−VB=Z2
Z1+ Z2
E
d’où VD−VC=1
n+ 1 −Z2 Z1+ Z2E
Eth =Z1−nZ2
(n+ 1) (Z1+ Z2)E
Une autre méthode, efficace à coup sûr, consiste à utiliser la loi des nœuds
et la loi des mailles. On a ainsi
E = iDB (nR + R) et E = iCB (Z1+ Z2)
De plus iDB R = VD−VBet iCB Z2= VC−VB
d’où VD−VC=iDB R−iCB Z2
VD−VC=1
n+ 1 −Z2 Z1+ Z2E
Eth =Z1−nZ2
(n+ 1) (Z1+ Z2)E
ce qui mène bien au même résultat.
Remarquons que le choix, fait par l’énoncé, de représenter un générateur
de tension alternative par le symbole d’un générateur de tension continue
n’est pas des plus heureux. Nous conservons néanmoins cette notation qui
a le mérite de rappeler comment remplacer le générateur lors du calcul de
l’impédance équivalente d’un circuit : lorsqu’on enlève le cercle, le générateur
de tension se transforme en fil tandis que le générateur de courant fait office
d’interrupteur ouvert.
A B C D E
Téléchargé gratuitement sur www.Doc-Solus.fr .

c
Éditions H&K Publié dans les Annales des Concours 4/18
2Pour calculer l’impédance équivalente, on éteint les sources indépendantes du
circuit en remplaçant les sources de tension par des fils et les sources de courant par
des interrupteurs ouverts. Ici, seule la source de tension Edevient un fil et on a
qui devient
avec 1
Req
=1
R+1 nRet 1 Zeq
=1
Z1
+1
Z2
où l’on somme les conductances car il s’agit de montages parallèles. Il ne reste plus
qu’à additionner les impédances restantes (assemblées en série) pour obtenir
Zth =nR
n+ 1 +Z1Z2 Z1+ Z2
A B C D E
3Le courant est nul dans la branche CD lorsque
Eth = 0
c’est-à-dire Z1=nZ2
ou encore Z1Y2=n
Un condensateur C1en série avec une résistance R1a une impédance
Z1= ZC1+ ZR1=1
jC1ω+ R1
Un condensateur C2en parallèle avec une résistance R2a une conductance
Y2= YC2+ YR2=jC2ω+1
R2
La condition d’équilibre Z1Y2=ns’écrit alors
1
jC1ω+ R1jC2ω+1 R2=n
Téléchargé gratuitement sur www.Doc-Solus.fr .