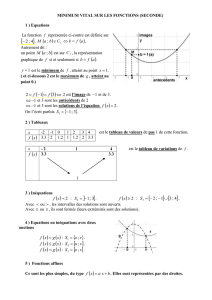
1. Rappels théoriques : résolution d`équations aux différences

MODÉLISATION ET SIMULATION
EQUATIONS AUX DIFFÉRENCES (I/II)
1. Rappels théoriques : résolution d’équations
aux différences
1.1. Équations aux différences.
Définition. Soit xk=x(k)∈Xl’état scalaire d’un système
dynamique à l’instant k∈Net f:N×Xn→Xune fonction
connue. L’équation récursive
x(k+n) = f(k, x(k+n−1), . . . , x(k))
est appelé équation aux différences d’ordre nen forme nor-
male.
Théorème. L’équation admet une et une solution une fois
fixées nvaleurs initiales. Notons qu’aucune autre restriction
sur la forme de fest posée.
1

MODÉLISATION ET SIMULATION EQUATIONS AUX DIFFÉRENCES (I/II) 2
1.2. Equation aux différences linéaire.
Définition. Une équation aux différences est dite linéaire
d’ordre n, avec n > 0, si elle a la forme
(1.1)
an(k)x(k+n)+an−1(k)x(k+n−1)+···+a0(k)x(k) = g(k)
où les fonctions ai(k), i = 0, . . . , n et g(k)sont données.
– Si les coefficients ne dépendent pas de kl’équation est
dite invariante (ou stationnaire). Si g(k) = 0 pour tout
kalors l’équation
(1.2)
an(k)x(k+n) + an−1(k)x(k+n−1) + ··· +a0(k)x(k) = 0
est dite homogène.
– La condition initiale d’une équation aux différences li-
néaire d’ordre nest le vecteur de taille [n, 1]
x0= [x(0), . . . , x(n−1)]

MODÉLISATION ET SIMULATION EQUATIONS AUX DIFFÉRENCES (I/II) 3
1.3. Solutions.
Théorème. Considérons l’équation linéaire non homogène (1.1)
et sa solution particulière x(p)(k). Soit x(h)(k)une solution de
l’équation homogène associée (1.2). Toutes les solutions x(k)
de l’équation linéaire non homogène peuvent être exprimées
sous la forme
x(k) = x(p)(k) + x(h)(k)
Le principe de superposition suivant est valable
Théorème. Si x(1)(k), x(2)(k), . . . , x(m)(k)sont solutions de
l’équation (1.2), alors chaque combinaison linéaire
c1x(1)(k) + c2x(2)(k) + ··· +cmx(m)(k)
où c1, . . . , cmsont des constantes arbitraires, est aussi une
solution de (1.2).

MODÉLISATION ET SIMULATION EQUATIONS AUX DIFFÉRENCES (I/II) 4
1.4. Exemple. Considérons l’équation
(k+ 1)x(k+ 1) −kx(k) = 1, k ≥1
dont l’équation homogène correspondante est
(k+ 1)x(k+ 1) −kx(k)=0.
La solution de l’équation homogène est
x(h)(k) = A/k
.
Une solution particulière est
x(p)(k) = 1
La solution a donc la forme
x(k) = 1 + A/k

MODÉLISATION ET SIMULATION EQUATIONS AUX DIFFÉRENCES (I/II) 5
1.5. Solutions fondamentales. Construisons un ensemble
de nsolutions x(i)(k),i= 1, . . . , n telles que
x(i)(0) = 0, . . . , x(i)(i−1) = 1, x(i)(i)=0, . . . , x(i)(n−1) = 0
Cet ensemble est appelé ensemble fondamental.
Théorème. Chaque solution de l’équation homogène (1.2)
peut être exprimée comme combinaison linéaire
c1x(1)(k) + c2x(2)(k) + ··· +cnx(n)(k)
des nsolutions fondamentales x(i)où c1, . . . , cnsont des constantes.
Le théorème suivant énonce que le rôle des nsolutions fon-
damentales peut être joué par un quelconque ensemble de n
solutions linéairement indépendantes :
Théorème. Chaque solution de l’équation homogène (1.2)
peut être exprimée comme combinaison linéaire
c1x(1)(k) + c2x(2)(k) + ··· +cnx(n)(k)
des nsolutions linéairement indépendantes x(i)où c1, . . . , cn
sont des constantes.