GÉNÉRALITÉS SUR LES FONCTIONS CHAPITRE 6 : I) Notion de fonction

CHAPITRE 6 : GÉNÉRALITÉS
SUR LES FONCTIONS
I) Notion de fonction
Définition
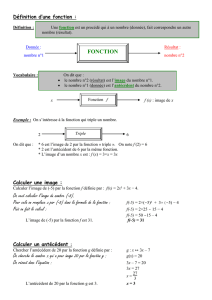
Soient x et y deux nombres relatifs. Une fonction est un processus mathématique qui, à un
nombre x, associe un unique nombre y.
x
y
Exemples :
La formule permettant de calculer l’aire d’un carré connaissant la longueur d’un côté est une fonction.
La fonction qui, à un nombre, fait correspondre le triple de ce nombre est une fonction.
Une fonction peut être défini par :
II) Notations et vocabulaire
a) Notations
La fonction qui, au nombre x, associe le nombre y se note :
f : x y (se lit : « fonction f qui à x associe y ») ou
f(x) = y (se lit « f de x est égal à y »).
On note aussi f : x
f(x) car dans ce cas
x, y et f(x) sont des nombres tandis que f n’est pas un nombre, c’est une fonction.
b) Vocabulaire
On dit que l’image de x par la fonction f est y.
L’image de x par la fonction f se note f(x). Cette image est unique.
On dit que x est un antécédent de y par la fonction f.
Un nombre peut avoir plusieurs antécédents.
Exemples : Soit f : x
x² qui se note également f(x) = x²
L’image de 4 par f est 4², c’est-à-dire 16.
4 est un antécédent de 16 par f.
f(4) = f(-4) = (-4)² = 16. Donc, (-4) est un autre antécédent de 16 par f.
Remarque : f(x) = x² est la forme algébrique de la fonction f.
III/ Représentation graphique d’une fonction
Soit a un nombre et f(a) son image par la fonction f.
Dans un repère, on considère les points M de coordonnées (a ; f(a)).
L’ensemble C f de ces points est la représentation graphique de la fonction f dans ce repère.
Exemple : Voici ci-dessous la courbe représentative Cf d’une fonction f.
Image de 1 par la fonction f : On cherche l’ordonnée du point de la courbe dont l’abscisse est 1.
L’image de 1 par f est 2, c’est-à-dire : f(1)=2
Antécédent de 3,5 par la fonction f : On cherche l’abscisse du (ou des) point(s) de la courbe qui a
(ont) pour ordonnée 3,5.
Un antécédent de 3,5 par f est 2 car f(2)=3,5.
Les antécédents de 2 par f sont : 1 et 3.