SHERBRQOKE LOIS DE COMMANDE PREDICTIVES AUTONOMES POUR

SHERBRQOKE
Faculte de genie
Departement de genie electrique
LOIS DE COMMANDE PREDICTIVES AUTONOMES POUR
VOL EN FORMATION DE SATELLITES TERRESTRES
Memoire de mattrise en sciences appliquees
Specialite : genie electrique
Composition du Jury:
Jean de Lafontaine ing., Ph.D
Aymeric Kron, ing., Ph.D
Gerard Lachiver ing., Ph.D
Vincent Simard Bilodeau
Sherbrooke (Quebec), Canada
\ \J-\\W
Ete 2008
9qn.es Wancher; TJ p,G^)
lasssir teA qu.e.1 •

1*1 Library and
Archives Canada
Published Heritage
Branch
395 Wellington Street
Ottawa ON K1A0N4
Canada
Bibliotheque et
Archives Canada
Direction du
Patrimoine de I'edition
395, rue Wellington
Ottawa ON K1A0N4
Canada
Your file Votre reference
ISBN: 978-0-494-49585-8
Our file Notre reference
ISBN: 978-0-494-49585-8
NOTICE:
The author has granted a non-
exclusive license allowing Library
and Archives Canada to reproduce,
publish, archive, preserve, conserve,
communicate to the public by
telecommunication or on the Internet,
loan, distribute and sell theses
worldwide, for commercial or non-
commercial purposes, in microform,
paper, electronic and/or any other
formats.
AVIS:
L'auteur a accorde une licence non exclusive
permettant a la Bibliotheque et Archives
Canada de reproduire, publier, archiver,
sauvegarder, conserver, transmettre au public
par telecommunication ou par Plntemet, prefer,
distribuer et vendre des theses partout dans
le monde, a des fins commerciales ou autres,
sur support microforme, papier, electronique
et/ou autres formats.
The author retains copyright
ownership and moral rights in
this thesis. Neither the thesis
nor substantial extracts from it
may be printed or otherwise
reproduced without the author's
permission.
L'auteur conserve la propriete du droit d'auteur
et des droits moraux qui protege cette these.
Ni la these ni des extraits substantiels de
celle-ci ne doivent etre imprimes ou autrement
reproduits sans son autorisation.
In compliance with the Canadian
Privacy Act some supporting
forms may have been removed
from this thesis.
Conformement a la loi canadienne
sur la protection de la vie privee,
quelques formulaires secondaires
ont ete enleves de cette these.
While these forms may be included
in the document page count,
their removal does not represent
any loss of content from the
thesis.
Canada
Bien que ces formulaires
aient inclus dans la pagination,
il n'y aura aucun contenu manquant.

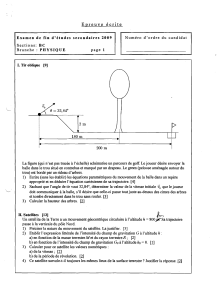
RESUME
Les technologies spatiales evoluent actuellement vers la fabrication de plusieurs microsatellites
autonomes volant en formation plutot que vers la construction de gros satellites. Cette strategie est
avantageuse. Par exemple, elle permet d'accrottre la resolution des mesures en correlant les signaux
provenant des instruments scientifiques des microsatellites. Cette antenne synthetique de grande
ouverture serait impossible a deployer avec un seul satellite.
Pour profiter des avantages de cette strategie, des lois de commande optimales (a au sens du temps
et du cout en propergol) et autonome qui permettent de maintenir et de reconfigurer une formation
doivent etre developpees. Ce travail de recherche s'interesse a ce sujet. Plus precisement, il traite des
aspects suivants:
1. Pour developper la loi de commande d'un systeme, il est necessaire de savoir le modeliser. Ce
document debute done par une presentation des modeles dynamiques les plus utilises pour
decrire le mouvement relatif entre deux satellites volant en formation sur une orbite terrestre.
2. Plusieurs auteurs se sont interesses a asservir une formation de satellites, les plus importantes
de celles-ci sont presentees dans ce document. Par cette etude de la litterature, le candidat
demontre que les lois de commande predictives sont des solutions efficaces comportant
plusieurs avantages. Par exemple, ces approches sont optimales et permettent de traiter des
contraintes sur les entrees et les sorties du systeme asservi.
3. En lien avec ce qui precede, une etude detaillee de la theorie des lois de commande predictives
lineaires et non lineaires discretes est presentee.
4. Par la suite, ces lois de commande predictives sont appliquees sur un systeme simple, soit une
grue a trois axes. Ces exemples ont ete developpes pour accroftre I'expertise de I'auteur dans
ce domaine ainsi que pour presenter les avantages et les performances des lois de commande
predictives.
5. Finalement, ce document presente le developpement d'une loi de commande predictive pour
le vol en formation de satellites basee sur le modele de Lawden et de GVE (Equations de
Variation de Gauss) linearisees. Les precedentes approches basees sur ce type de loi de
commande reposaient sur I'optimisation de I'effort de commande soumis a des contraintes sur
les entrees et les sorties du systeme en utilisant un algorithme complexe et non autonme pour
maintenir et reconfigurer la formation. La technique proposee est plutot de minimiser une

fonction cout quadratique incluant directement les erreurs relatives futures, et ce, en
considerant des contraintes sur les actionneurs (contraintes sur les entrees du systeme). La
commande optimale est obtenue avec un algorithme analytique base sur la projection de la
fonction cout sur les contraintes permettant ainsi de reduire considerablement le temps de
calcul.
Mots cles: formation de satellites, grue a trois axes, lois de commandes predictives, optimisation
quadratique explicite avec contraintes, satellites autonomes, orbites excentriques.