reactions acido basiques cours

Réactions acido-basiques
1
Le pH des solutions aqueuses :
Autoprotolyse de l'eau
• Équation d'autoprotolyse
Nous savons, depuis la classe de Première, que l'eau
est un ampholyte acido-basique, c'est-à-dire qu'elle
est l'acide d'un couple (H2O/HO–) et la base d'un
autre couple (H3O+/H2O).
Les demi-équations associées à ces couples s'écrivent :
H2O(ℓ) = HO–(aq) + H+(aq) (1)
H2O(ℓ) + H+(aq) = H3O+(aq) (2)
En formant (1) + (2), on obtient l'équation de la
réaction acido-basique de l'eau sur elle-même.
L'eau participe à un équilibre chimique appelé
autoprotolyse dont l'équation s'écrit :
2 H2O(ℓ) = H3O+(aq) + HO–(aq)
L'eau, même la plus purifiée, contient donc toujours,
en quantité infime, des ions oxonium et hydroxyde.
D'après la stœchiométrie de l'équation, on voit que les
quantités d'ions oxonium et hydroxyde formés par cet
équilibre sont égales.
Dans l'eau pure, on a :
[H3O+]f = [HO–]f .
Cette égalité n'est valable que pour l'eau pure. Ainsi,
dans une solution aqueuse quelconque, contenant par
exemple un autre couple acide/base, on peut avoir :
[H3O+]f [HO–]f .
• Produit ionique
Comme pour tout équilibre, on caractérise l'équilibre
d'autoprotolyse de l'eau par une constante
d'équilibre ne dépendant que de la température.
La constante d'équilibre Ke associée à l'équation
d'autoprotolyse de l'eau est appelée produit ionique
de l'eau et s'écrit : Ke = [H3O+]f . [HO–]f.
Cette relation est vérifiée pour toutes les solutions
aqueuses.
Elle est très utile, notamment pour la détermination
du pH d'une solution aqueuse.
Ke ne dépend que de la température ; on retient sa
valeur à 25 °C : Ke = l,0.10–14.
On définit la grandeur logarithmique suivante,
associée au produit ionique de l'eau :
pKe = – log Ke soit : Ke == 10–pKe.
pKe, tout comme Ke, ne dépend que de la
température. pKe = 14 à 25 °C.
Échelle de pH
• Solution neutre, acide ou basique
Suivant la valeur de son pH, une solution aqueuse
présente un caractère neutre, acide ou basique.
• Une solution neutre contient autant d'ions oxonium
que d'ions hydroxyde : [H3O+]f = [HO–]f
• Une solution acide contient plus d'ions oxonium
que d'ions hydroxyde : [H3O+]f > [HO–]f
• Une solution basique contient moins d'ions
oxonium que d'ions hydroxyde :
[H3O+]f < [HO–]f
On peut alors, grâce au produit ionique de l'eau, relier
le caractère neutre, acide ou basique d'une solution à
la valeur de son pH.
À 25 °C, le pH est :
– égal à 7,0 dans une solution neutre ;
– strictement inférieur à 7,0 dans une solution acide ;
– strictement supérieur à 7,0 dans une solution
basique.
Exemples :
À 25 °C,
– l'eau distillée qui est une solution neutre, a un pH
égal à 7,0 ;
– une solution d'acide éthanoïque qui est acide, a un
pH inférieur à 7,0 ;
– une solution d'ammoniac qui est basique, a un pH
supérieur à 7,0.
• Représentation graphique
On peut représenter graphiquement la propriété
précédente à l'aide d'une échelle de pH.
On se limite en pratique à une échelle pour laquelle
0 < pH < 14, domaine où la relation pH = – log[H3O+]
s'applique.
METHODE
Déterminer le pH d'une solution
1. Écrire l'équation de la réaction acido-basique
ayant lieu en solution.
2. Établir le tableau d'avancement correspondant.
3. Deux cas se présentent :
– si H3O+ fait partie des produits, déterminer sa
concentration finale et en déduire le pH ;
– si HO– fait partie des produits, déterminer sa
concentration finale puis en déduire celle des ions
oxonium par le biais du produit ionique de l'eau.
Enfin, déterminer le pH de la solution.
0
7
14
pH à
25°C
solutions
neutres
solutions basiques
solutions acides

Réactions acido-basiques
2
Exemple :
Soit une solution d'ammoniac, de concentration
C égale à 1,0.10–2 mol.L–1. Le taux d'avancement
final de la réaction est 4,0 %. Déterminons le pH de
cette solution dont la température est de 25 °C.
1. La réaction de l'ammoniac sur l'eau a pour
équation : NH3(aq) + H2O(ℓ) = NH4+(aq) + HO–.
2. Le tableau d'avancement correspondant s'écrit, en
raisonnant sur un litre de solution :
Equa-
tion
NH3(aq) + H2O(ℓ) = NH4+(aq) + HO–.
état …
Avan-
cement
Quantité de matière (mol)
initial
0
1,0.10–2
bcp
0
0
intermé
diaire
x
1,0.10–2 – x
bcp
x
x
final
xf
1,0.10–2 – xf
bcp
xf
xf
3. Le taux d’avancement final de la réaction est égal à
4%, soit : τ = xf
xmax = [HO–]f C = 4,0.10–2. Donc
[HO–]f = C.τ = 1,0.10–2 × 4,0.10–2 = 4,0.10–4 mol.L–1
Or Ke = [H3O+]f . [HO–]f = 1,0.10–14
donc [H3O+]f = Ke
[HO–]f = 1,0.10–14 4,0.10–4 = 2,5.10–11 mol.L–1
On en déduit : pH = – log (2,5.10–11) = 10,6
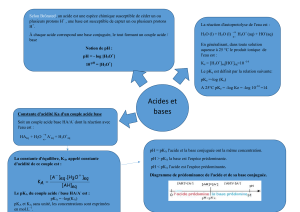
Comparaison des acides et des bases
Constante d'acidité
Dans I Qr/K, nous avons défini de manière générale
la constante d'équilibre associée à l'équation d'une
réaction. Dans le cas d'une réaction d'un acide sur
l'eau, cette constante porte un nom particulier que
nous allons à présent introduire.
L'équation de la réaction d'un acide HA sur l'eau
s'écrit : HA(aq) + H2O = A–(aq) + H3O+
La constante d'équilibre associée à l'équation de la
réaction d'un acide sur l'eau est appelée constante
d'acidité KA du couple HA/A– :
KA = [H3O+]f [A–]f
[HA]f
On associe à KA la grandeur logarithmique notée pKA
définie par : pKA = – log KA.
Cette dernière égalité équivaut à :
KA= 10–pKA.
La valeur de KA dépend de la nature du couple HA/A–
et de la température. Comme toute constante
d'équilibre, c'est une grandeur sans dimension.
Exemples : à 25 °C,
– pour le couple H3O+/H2O, pKA = 0,0 et KA = 1,0 ;
– pour le couple H2O/HO–, pKA = 14,0 et KA= 1,0.10–14;
– pour le couple CH3COOH /CH3COO–, pKA = 4,8 et
KA = 10 –4,8 = 1,6.10–5.
À partir de la définition de KA (en appliquant la
fonction – log aux deux membres), on en déduit la
relation suivante :
pH = pKA + log [A–]f
[AH]f
qui peut s'avérer très utile dans les exercices.
Comparaison des acides et des bases
On suppose ici que la seule réaction à considérer est
la réaction de l'acide (ou de la base) que l'on étudie
sur l'eau. On peut alors montrer les résultats suivants.
À concentration identique,
– la solution de l'acide du couple ayant la constante
d'acidité la plus grande (et donc le pKA le plus
petit) a le pH le plus petit ;
– la solution de la base du couple ayant la constante
d'acidité la plus grande (et donc le pKA le plus
petit) a le pH le plus petit.
KA et pKA varient en sens inverse l'un de l'autre.
On peut relier la constante d'acidité au taux
d'avancement final de la réaction de l'acide (ou de la
base) considéré.
À concentration identique, le taux d'avancement final :
– de la réaction d'un acide HA sur l'eau est d'autant
plus grand que la constante d'acidité du couple auquel
il appartient est grande (et donc le pKA est petit) ;
– de la réaction d'une base A– sur l'eau est d'autant
plus petit que la constante d'acidité du couple auquel
elle appartient est grande (et donc le pKA est petit).
Exemples :
Soient les deux couples suivants :
CH3COOH/CH3COO– de KA = 1,6.10–5 et de
pKA = 4,8 ;
NH4+/NH3 de KA = 6,3.10–10 et de pKA = 9,2.
– A concentration identique, le pH d'une solution
d'acide éthanoïque CH3COOH est plus petit que celui
d'une solution de chlorure d'ammonium NH4Cl. Par
ailleurs, le taux d'avancement final de la réaction de
l'acide éthanoïque sur l'eau est plus grand que celui
de la réaction des ions ammonium sur l'eau.
– À concentration identique, le pH d'une solution
d'éthanoate de sodium NaCH3COO est plus petit que
celui d'une solution d'ammoniac NH3 Par ailleurs, le
taux d'avancement final de la réaction des ions
éthanoate sur l'eau est plus petit que celui de la
réaction de l'ammoniac sur l'eau.
Constante d'équilibre d'une réaction acido-basique
On considère la réaction entre l'acide HA1 du couple
HA1/A1–, et la base A2 du couple HA2/A2–. Cette
réaction mène à un équilibre dont l'équation s'écrit :
HA1 + A2– = A1– + HA2
Sa constante d'équilibre a pour expression :
K = [HA2]f . [A1–]f
[HA1]f . [A2–]f

Réactions acido-basiques
3
En introduisant les constantes d'acidité KA1 et KA2
relatives à ces deux couples, on aboutit à la propriété
suivante.
Soit l'équilibre acido-basique mettant en jeu les
couples acide 1 /base 1 de constante d'acidité KA1 et
acide 2/ base 2 de constante d'acidité KA2 , dont
l'équation s'écrit :
acide 1 + base 2 = acide 2 + base 1.
La constante d'équilibre associée à cette réaction
s'écrit : K = KA1
KA2
Exemple :
La réaction entre l'acide éthanoïque (KA1 = 1,6.10–5)
et l'ammoniac (KA2 =5,6.10–10) a pour équation :
CH3COOH + NH3 = CH3COO– + NH4+
On en déduit la valeur de sa constante d'équilibre :
K = 1,6.10–5
5,6.10–10 = 2,9.104
On peut également définir le pK de la réaction acido-
basique étudiée ; on a alors :
pK = pKA1 – pKA2.
METHODE
Déterminer à partir de la constante d'équilibre si
une transformation est totale
Après avoir écrit l'équation de la réaction considérée,
on calcule sa constante d'équilibre K.
Trois cas se présentent alors :
• Si K ≥ 104, la transformation associée est
considérée comme totale.
• Si K 1, la transformation mène à un état
d'équilibre.
• Si K ≤ 10–4, la transformation est très peu avancée.
Il ne s'agit que d'ordres de grandeur; les valeurs
frontières de 104 et 10–4 pourront parfois être
légèrement différentes suivant l'exercice considéré,
Exemple :
La réaction de l'acide éthanoïque sur l'ammoniac dont
nous avons calculé la constante d'équilibre K, égale à
2,9.104 peut être considérée comme totale.
La réaction inverse d'une réaction pouvant être
considérée comme totale est très peu avancée
puisque sa constante d'équilibre K' est égale à
l'inverse de K (si K ≥ 104, alors 1
K ≤ 10–4)
w
Prédominance et distribution des espèces
acido-basiques
Diagrammes de distribution et de prédominance
Expérimentalement, on met en évidence l'existence
de domaines de pH dans lesquels l'une des formes,
acide ou basique, d'un couple acide/base prédomine
et d'un domaine dans lequel elles coexistent en
proportions comparables.
Un diagramme de distribution représente les
variations des pourcentages de la forme acide HA et
de la forme basique A– d'un couple acido-basique en
fonction du pH de la solution.
Le diagramme de prédominance partage l'échelle
de pH en deux zones :
– une zone dans laquelle la forme acide HA du
couple prédomine : [HA]f > [A–]f ;
– une zone dans laquelle la forme basique A– du
couple prédomine : [A–]f > [HA]f.
Pour une solution aqueuse contenant les espèces HA
et A–, on sait que : pH = pKA + log [A–]f
[HA]f
On en déduit immédiatement la propriété suivante :
• Si pH < pKA, alors [A–]f
[HA]f < 1 donc [HA]f > [A–]f :
la forme acide prédomine en solution.
• Si pH = pKA, alors [A–]f
[HA]f = 1 donc [HA]f = [A–]f :
les formes acide et basique ont des concentrations
molaires finales identiques.
• Si pH > pKA, alors [A–]f
[HA]f > 1 donc [HA]f < [A–]f :
la forme basique prédomine en solution.
On peut représenter graphiquement les diagrammes
de distribution et de prédominance pour un couple
HA/A– comme suit.

Réactions acido-basiques
4
Application aux indicateurs colorés acido-
basiques
Nous avons déjà rencontré la notion d'indicateur
coloré en Première, notamment à l'occasion de
l'étude des dosages.
• Indicateur coloré acido-basique
Un indicateur coloré acido-basique est un couple
acide/base dont les deux formes acide et basique
sont de couleurs différentes.
On note ce couple HInd/Ind– et sa constante
d'acidité Kind.
• Zone de virage
Pour fixer les idées, on considère que seule la teinte
de l'une des formes est visible lorsque la
concentration de cette forme est au moins dix fois
plus grande que celle de l'autre forme, ce qui mène
à la propriété suivante.
• Si pH < pKind – 1, la solution a la couleur de la
forme acide.
• Si pH > pKind + 1, la solution a la couleur de la
forme basique.
Lorsque le pH de la solution est compris entre
pKind – 1 et pKind + 1, les deux espèces Hind et Ind–
sont mélangées et la couleur de la solution est
intermédiaire entre celle de la forme acide et celle
de la forme basique.
On appelle zone de virage d'un indicateur coloré le
domaine de pH s'étendant approximativement sur
deux unités pH de part et d'autre du pKA, noté
pKind, du couple Hind/Ind–.
Dans la zone de virage, la solution contenant
l'indicateur coloré prend une couleur appelée teinte
sensible de l'indicateur, intermédiaire entre celles
de la forme acide et de la forme basique.
L'étendue ainsi définie sur deux unités pH de la
zone de virage est approximative ; l'énoncé peut
donner une zone de virage légèrement plus grande
ou plus petite pour un indicateur coloré donné
Exemple : le bleu de bromothymol (BBT) Le BBT a
un pKind égal à 7,1.
Les manuels donnent souvent une zone de virage du
BBT de [6,0; 7,6], plus restreints que celle
proposée ici.
• Utilisation
En utilisant successivement plusieurs indicateurs
colorés, judicieusement choisis, on peut évaluer
approximativement le pH d'une solution aqueuse.
Une utilisation particulièrement intéressante d'un
indicateur coloré est surtout le repérage du point
équivalent lors d'un dosage, comme on l'a vu en
Première. Ce point sera revu et approfondi dans
I Titrages
METHODE
Déterminer l'espèce prédominante dans une
solution aqueuse
• Faire l'inventaire des espèces chimiques
présentes dans la solution.
• Déterminer le pH et/ou prendre en compte la
couleur de la solution.
• Comparer le pH au pKA du couple acido-
basique présent et/ou comparer la couleur de la
solution aux couleurs des formes acide et basique
du couple.
Si pH < pKA, la forme acide prédomine, sinon la
forme basique prédomine.
Exemple :
Considérons une solution contenant les espèces du
couple NH4+/NH3, auxquelles on a ajouté quelques
gouttes de BBT. La solution prend une coloration
jaune.
Donnée : pKA(NH4+/NH3) = 9,25 ;
La zone de virage du BBT comprise entre 6,0 et 7,6
est la zone où il passe du jaune au bleu.
La coloration jaune du BBT indique que le pH de la
solution est inférieur à 6,0. Cette valeur est
inférieure à 9,25, le pKA du couple NH4+/NH3,.
L'ion ammonium est donc l'espèce prédominante
dans cette solution
7,1
14
pH
PKind
coloration bleue
forme acide
forme basique
coloration jaune
6,1
8,1
zone de virage
coloration
intermédiaire
0