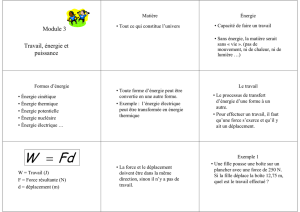
Nous allons ici aborder la notion d’énergie qui joue un... et techniques aussi bien que sur le plan sociétal.

1
Nous allons ici aborder la notion d’énergie qui joue un rôle central dans le domaine des sciences
et techniques aussi bien que sur le plan sociétal.
2
La notion d’énergie n’est pas facile à appréhender.
Nous en avons toutefois une vision subjective grâce à nos expériences de vie quotidienne.
C’est ce qu’illustrent les photos ci-dessus.
Ces photos montrent des situations de la vie de tous les jours dans lesquelles nous fournissons
un effort, nous dépensons de l’énergie.
Chacune de ces situations ont un point commun, c’est la combinaison d’une force et d’un
déplacement.
Cette combinaison est illustrée avec la photo de la personne qui monte un escalier: la force
exercée vers le haut par les muscles de la jambe est accompagnée d’un mouvement vers le haut.
Il en est de même pour tous les exemples que l’on voit.
D’un point de vue intuitif on pourrait donc dire que l’énergie résulte de la combinaison d’une
force et d’un déplacement (le déplacement étant dû à la force elle-même).
3
Le déplacement ne semble cependant pas indispensable pour dépenser de l’énergie car, même
pour exercer une force de façon statique nous dépensons de l’énergie.
Mais ceci est dû au fait que nos muscles ne sont pas des dispositifs parfaits et que, en
l’occurrence, ils dépensent de l’énergie pour rester simplement contractés de façon statique.
Ceci est illustré ici avec le schéma d’un bras portant un poids.
4
Mais cette simple action de porter de façon statique ne demande en réalité pas d’énergie.
Pour s’en rendre compte il suffit de remplacer le bras par un support solide comme le socle
cylindrique représenté ici.
Il est évident que dans cette situation il n’y a pas d’énergie dépensée.
Il en serait de même pour nous si nos muscles pouvaient se bloquer sans plus demander
d’alimentation en sucre et en oxygène.
5
Il en est de même quand nous poussons sur un mur.
Nous avons le sentiment que cette action requiert de l’énergie mais il n’en est rien.
6
Pour le comprendre il suffit d’imaginer que l’on remplace la main qui pousse par un objet pesant
s’appuyant sur le mur.
A nouveau on voit clairement qu’exercer une force ne suffit pas à dépenser de l’énergie.
7
Nous en concluons que l’énergie est bien le résultat de la combinaison d’une force et d’un
déplacement (dû à cette force).
Nous dirons de façon un peu schématique que l’énergie est le résultat de « forces en
déplacement ».
8
Cette vision de l’énergie comme étant le résultat de la combinaison d’une force et d’un
déplacement est universelle et on la retrouve dans toutes les formes d’énergie.
Considérons par exemple l’énergie calorifique symbolisée ici par le fer à repasser et le radiateur.
9
Si on étudie ce qui se produit à l’échelle microscopique dans ces appareils électriques on voit des
électrons qui constituent le courant électrique traversant les résistances chauffantes.
Dans leur mouvement les électrons rentrent en collision avec les atomes de la résistance.
Les collisions engendrent une force sur les atomes (flèche rouge sur le schéma ci-dessus) et
ceux-ci se déplacent sous l’effet de ces forces, ce qui provoque un accroissement de l’agitation
des atomes autour de leur position d’équilibre.
Cette agitation n’est rien d’autre que la chaleur.
On voit ainsi que la chaleur est due à des forces en déplacement (processus de collision).
10
Le principe de fonctionnement de la résistance chauffante est illustré ici.
Le courant électrique est représenté par les flèches attachées aux électrons (responsables de
l’échauffement par collisions).
11
Bien sûr l’énergie d’agitation thermique provient de l’énergie des électrons (ou du courant
électrique).
On peut se demander dès-lors d’où vient l’énergie du courant électrique.
A nouveau la réponse se trouve dans l’action d’une force en déplacement.
En effet le courant électrique est créé dans des fils conducteur en déplaçant ces fils dans un
champ magnétique.
Le parallélépipède rectangle représente ici un aimant.
Si le fil électrique est tiré vers le bas à l’aide d’une force (flèche rouge) il se déplacera vers le bas
dans le champ magnétique de l’aimant et les électrons subiront alors une force magnétique qui
les tire vers la droite pour créer le courant électrique (voir cours de physique générale)
responsable de l’échauffement.
A nouveau, on voit que l’énergie électrique provient de l’action d’une force en mouvement.
12
Ce principe est universel. Il est vrai pour les éoliennes par exemple.
Dans ce cas ce sont les molécules de l’air qui engendre des forces par collisions sur les pales de
l’éolienne dans laquelle on trouve un générateur électrique (illustré en bas à gauche) constitué
de fils électrique en déplacement dans un champ magnétique.
Pour les centrales hydroélectriques c’est la même chose à part que ce sont les molécules d’eau
qui engendre les forces qui permettent de faire tourner le générateur électrique (on voit la
turbine dans laquelle ces forces sont à l’œuvre en bas à droite).
13
Une fois cette idée acquise on peut rechercher comment l’énergie dépend du déplacement et de
la force qui cause ce déplacement.
Nous noterons l’énergie par la lettre « W » qui vient de « work » qui signifie travail en anglais.
Le mot travail traduit ici la notion d’énergie dans la mesure où il rappelle l’idée d’effort
musculaire.
Nous parlerons donc ici indifféremment d’énergie ou de « travail ».
Pour trouver l’expression du travail « W » en termes de la force « F » et de la longueur du
déplacement « L », considérons une situation simple dans laquelle on déplace un objet avec une
force « F » sur une longueur « L ».
Supposons par exemple que l’on doive lever une masse de poids « P » d’une hauteur « L=H ».
Cette action nous demande de façon évidente un effort, c’est à dire, de l’énergie.
Nous appellerons l’énergie nécessaire « W0 » ce sera l’énergie de référence pour notre
raisonnement.
14
Si on lève le poids « P » sur une hauteur deux fois plus grande, on dépense de façon évidente
deux fois plus d’énergie et ceci peut se généraliser à n’importe quel facteur multiplicatif.
Il est donc évident que le travail est proportionnel à la longueur du déplacement, comme indiqué
sous la ligne ci-dessus.
15
Si maintenant nous collons les poids l’un à l’autre et que l’on répète l’opération, c’est-à-dire
qu’on lève l’ensemble avec les deux bras.
16
On exercera une force totale « 2P » et l’énergie dépensée est bien sûr la même que quand les
blocs étaient détachés (le fait que les blocs soient collés n’a pas modifié notre effort).
On voit donc que la force « 2P » exercée sur une longueur « H » correspond à une énergie
« 2W0 », ce qui nous permet de conclure que le travail est également simplement proportionnel à
la force, comme indiqué sous la ligne ci-dessus.
17
On peut exprimer ces deux lois de proportionnalité en une seule en disant que le travail est égal
au produit de la force par la longueur sur laquelle elle se déplace.
18
Passons maintenant à la généralisation de l’expression du travail. L’écriture « W = F.L » n’est
effectivement pas toujours adaptée. Sur ce slide, la longueur du déplacement « L » est remplacée
par la différence des coordonnées extrêmes du déplacement, soit « L= x f − x i » où « x i » est la
coordonnée initiale de l’objet et « x f » est la coordonnée finale de l’objet. On peut également
l’écrire « Δx » de sorte que l’expression du travail devienne « W = F. Δx ».
Cette écriture est intéressante dans la mesure où elle permet de tenir compte du sens du
déplacement. Si le déplacement se fait vers le haut (dans le même sens que la force) alors
« xf > xi » et le produit « F. Δx » est positif. C’est la situation illustrée en haut à droite. Le travail
qui y correspond « W = F. Δx » est positif.
Lorsque le déplacement a lieu vers le bas alors « x f < x i » et le produit « F. Δx » est négatif. C’est
la situation illustrée en haut à gauche. Le travail qui y correspond « W = F. Δx » est négatif.
Comme l’illustre le skieur (nautique), cette situation de travail négatif correspond à la situation
où le travail est reçu par l’utilisateur. Le skieur reçoit l’énergie dans la mesure où la force qu’il
exerce lui permet d’avancer.
Dans la situation du travail négatif de gauche, celui qui exerce la force effectue le déplacement à
la force de ses muscles. C’est lui qui fournit le travail.
On voit ainsi apparaître naturellement une convention de signe. Quand force et déplacement ont
lieu dans le même sens le travail est positif et correspond à une énergie fournie tandis que quand
force et déplacement ont lieu en sens opposés le travail est négatif et correspond à une énergie
reçue.
19
Cette convention impose en réalité de donner un signe à la force également.
En effet, on peut facilement imaginer un déplacement vers les « x » positifs en même temps
qu’une force dirigée vers les « x » négatifs.
Dans ce cas, force et déplacement sont opposés et le travail résultant est un travail reçu qui selon
la convention doit être négatif.
C’est la situation du schéma inférieur gauche.
Dans ce cas d’après la formule « W = F.Δx » la force doit être définie négative.
Le schéma inférieur droit lui représente toujours la situation du skieur pour lequel le travail est
négatif.
En conclusion, on voit que déplacement et force doivent être définis avec des signes pour
répondre à la convention du travail fourni « W > 0 » ou reçu « W < 0 ». Sur le plan mathématique,
à la fois « F » et « Δx » sont des vecteurs, c’est d’ailleurs la raison pour laquelle ils sont notés à
l’aide de flèches sur les schémas.
Nous aurons l’occasion d’approfondir ces aspects plus loin.
20
Mais la formule du travail « W = F.Δx » n’est pas encore générale car elle ne peut pas être
appliquée dans le cas où la force varie au cours du déplacement. Prenons l’exemple d’un ressort
fixé à une extrémité, comme représenté ici. Si on laisse le ressort au repos, son extrémité droite
se trouve en « x = xi » (« i » pour position initiale). Si on exerce une force donnée, par exemple
« F=10 N », le ressort s’allonge. Si on augmente la force il s’allonge d’autant plus. Si on s’arrête
d’augmenter la force à « F = 20 N » on arrive à une position finale « x = xf ». Si on n’y prend pas
garde on serait tentés d’appliquer la formule « W = F.Δx », ce qui ne poserait pas de problème
avec « Δx » qui vaut « Δx = xf – xi » mais quelle valeur utiliser pour « F »? La valeur initiale qui est
nulle ou la valeur finale qui vaut 20 N. La réponse est bien entendu aucune des deux. La formule
du travail « W = F.Δx » n’a de sens que si la force est maintenue constante sur tout le
déplacement, c’est en tout cas dans ces conditions que nous l’avons construite.
On pourrait appliquer la formule « W = F.Δx » si on y considère des déplacements suffisamment
petits pour pouvoir négliger les variations de la force. Dans cette perspective, il apparaît naturel
d’exploité de formalisme du calcul différentiel de Newton.
Si on considère un déplacement infinitésimal « dx » entre les coordonnées « x » et « x+dx » il est
évident que l’on peut considérer la force constante puisque « dx » est par définition
arbitrairement petit. Le travail infinitésimal « dW » fourni sur cette distance peut donc être
donné par la formule à force constante qui donne ici « dW = Fdx ». Et le travail total est
simplement la somme de tous les travaux infinitésimaux dus aux déplacements infinitésimaux
contigus allant de « xi » à « xf ». L’expression du travail est donc l’intégrale de la force sur
l’intervalle « [ x i ,x f ] » telle qu’écrite en bas à droite.
Notez que cette intégrale représente l’aire sous le graphe de la force (voir aire colorée en vert
sur le graphe en haut à droite).
21
Mais qu’est-ce qu’une force au juste?
Il est difficile de répondre à cette question en dehors de l’idée intuitive que l’on se fait de la force
à partir de la notion d’effort musculaire.
La loi de Newton qui nous dit de façon assez abstraite que la force est une grandeur
proportionnelle à la masse et l’accélération d’un objet qui y est soumis dans l’espace libre mais
cela n’explique en rien la notion de force quant à sa nature ou son origine physique.
Les études de physiologie ont montré que la force musculaire est due à la contraction de
molécules complexes sous l’effet de réactions chimiques induites pas les influx nerveux du
cerveau.
Or les molécules trouvent leur cohésion dans la force électrique qui attire ou repousse les
atomes entre eux.
Ceci signifie que la force musculaire est un fait une force de nature électrique.
22
En fait dans la nature, il n’y a que trois grandes forces fondamentales, la force électrique, la force
gravitationnelle et la force nucléaire (souvent appelée l’interaction forte).
Toutes les forces qui s’exercent entre les composants de l’univers sont des forces qui impliquent
une ou plusieurs de ces trois forces fondamentales.
Ici est représentée la force d’attraction que la terre exerce sur la lune.
23
Considérons la force électrique qui attire l’électron (de charge électrique négative) sur le proton
(de charge électrique positive).
Si, par la pensée, on reliait ces deux particules par une petite tige. La tige subirait la force que
subit l’électron et on pourrait croire a priori que l’ensemble ainsi formé se déplacerait
spontanément dans l’espace en effectuant un MRUA (la force étant constante).
24
On pourrait également fixer la tige munie de ses deux charges électriques à un système
mécanique pour produire de l’énergie (force en déplacement pour effectuer une tâche telle que
lever un poids dans le champ gravitationnel de la terre par exemple).
On pourrait ainsi disposer d’une énergie infinie gratuite.
25
Mais malheureusement cela n’est bien sûr pas possible et la raison en est très simple: c’est que
toute force d’interaction entre particules de matière apparaît par couple de forces opposées.
C’est illustré ici avec la force électrique qu’exerce l’électron sur le proton : la tige subit une force
totale nulle et ne se déplace pas spontanément dans l’espace.
26
Et il en est bien sûr de même de toutes les forces quel que soit leur nature.
Les forces apparaissent toujours par couple de forces opposées.
La conséquence de cela est qu’il est impossible de créer de l’énergie à partir de rien.
En effet, si un travail positif est effectué par une force, la force opposée correspondante
effectuera un travail négatif (si le déplacement est dans le même sens que la première force, il
sera d’office dans le sens opposé à la deuxième force).
Cette remarque doit être complétée au cas où les particules (masses ou charges) en interaction
voient leur distance modifiée.
Nous verrons plus loin que cette situation correspond à la transformation du travail en d’autres
formes d’énergies.
Dans un système physique isolé de l’extérieur, l’énergie est une grandeur conservée.
On peut bien sûr communiquer de l’énergie de l’extérieur à un système physique (alors non
isolé) en y exerçant des forces, mais cette énergie sera inévitablement consommée à l’extérieur.
Il ne peut y avoir que des transferts ou des transformations d’énergie, mais pas de création pure
d’énergie.
C’est ce que l’on appelle le principe de conservation de l’énergie.
27
Le fait que les forces apparaissent par couple, implique une autre loi de conservation.
Pour le voir considérons deux particules matérielles (numérotées « 1 » et « 2 ») en interaction au
travers d’une des forces fondamentales de la nature.
La force « F1,2 » est la force que subit la particule « 1 » en raison de la présence de la particule
« 2 ». Et la force « F2,1 » est la force que subit la particule « 2 » en raison de la présence de la
particule « 1 ».
Comme nous venons de la voir on a toujours « F1,2 + F2,1 = 0 ».
Sur base de la loi de Newton, le développement ci-dessus montre très simplement que cette
relation de symétrie des forces implique que la quantité « m1v1 + m2v2 » ne dépend pas du temps,
soit « d(m1v1 + m2v2)/dt = 0.
On appelle « quantité de mouvement » le produit de la masse par la vitesse « m.v » et la relation
indique donc que la quantité de mouvement totale du système de deux particules est conservée.
On désigne la quantité de mouvement par la lettre « p » et on peut écrire « d(p1 + p2)/dt = 0 » ou
encore « dptot/dt = 0 » où « ptot » est la quantité de mouvement totale du système de deux
particules.
Remarquez que cette propriété n’est valable que si les particules ne subissent aucune autre force
de l’extérieur (le système doit être isolé de l’extérieur).
28
On peut généraliser le résultat à un système isolé comportant un nombre quelconque de
particules (ici numérotées par un indice allant de 1 à N).
Dans le développement ci-dessus, « Fm,n » est la force que subit la particule « m » en raison de la
présence de la particule « n ».
Cette force n’existe bien sûr que si « m » est différent de « n ».
Avec ces notation la relation de symétrie des paires de forces s’écrit « Fm,n + Fn,m = 0 ».
Si on écrit la loi de Newton pour chacune des particules en y introduisant la notion de quantité
de mouvement (c’est-à-dire, « mndvn/dt = dpn/dt » et que l’on somme toutes les relations
obtenues, on voit très facilement que la somme des dérivées des quantités de mouvement, c’est–
à-dire, la dérivée de la quantité de mouvement totale est nulle.
Autrement dit la quantité de mouvement totale d’un système de N particules isolées est une
grandeur conservée.
Nous verrons que cette loi de conservation est très précieuse en pratique pour résoudre des
problèmes de mécanique.
29
L’application du principe de conservation de l’énergie nous conduit au théorème de l’énergie
cinétique.
Son développement se base sur l’expression de la loi de Newton et l’expression mathématique du
travail.
Ce théorème s’applique au cas où l’on exerce une force à une masse libre de se mouvoir sans
frottement.
On peut effectivement dans ce cas, se poser la question de savoir ce que devient le travail
résultant du déplacement de la force.
Dans la perspective de la conservation de l’énergie, le travail est supposé se transformer en une
autre forme d’énergie, c’est cette nouvelle forme d’énergie que l’on va découvrir ici.
Comme le nom du théorème l’indique, il s’agit de l’énergie cinétique.
Nous considérons donc pour commencer une masse « m » à laquelle on exerce une force
quelconque « F(x) » sur l’intervalle de coordonnées « [xi,xf] ».
30
Le développement part de l’idée que l’énergie est conservée et donc nous partons de l’égalité
entre l’énergie cinétique et le travail fourni à la masse « m » en raison du déplacement de la force
« F(x) ».
Commençons par substituer l’expression de la force donnée par la loi de Newton dans l’intégrale
du travail.
On voit que l’intégrale contient le produit « (dv/dt)dx ».
Le schéma de droite illustre la signification des grandeurs qui apparaissent dans cette
expression. « dx » est la distance parcourue sur le temps « dt » et « dv » est l’accroissement de
vitesse acquis pendant ce déplacement.
Notez que le travail élémentaire exercé sur ce déplacement est donné
« dW = F.dx = m(dv/dt)dx » que l’on peut encore écrire « dW = F.dx = m(dx/dt)dv ».
par
Il est évident que le rapport « dx/dt » qui apparaît dans cette expression n’est autre que la
vitesse « v » elle-même.
Dans l’expression du travail total « SdW » on a donc en réalité affaire à l’intégrale de « vdv » qui
peut être calculée très facilement puisque la primitive est bien connue et vaut « v2/2 ». Le
résultat est donc évident « W = (m/2)(vf2-vi2) » où « vi » est la vitesse initiale et « vf » est la
vitesse finale obtenue au moment où le travail « W » est fourni entièrement.
31
Pour interpréter physiquement ce résultat, prenons le cas d’une vitesse initiale nulle « vi=0 » et
appelons « v » la vitesse finale, soit « vf = v ». On trouve alors « W = (m/2)v2 ».
D’après le principe de conservation de l’énergie, une fois le travail « W » fourni il est dépensé et
n’existe plus et il est donc remplacé par l’énergie cinétique qui caractérise la masse lorsqu’elle
est en mouvement à la vitesse finale « v ».
On peut donc en conclure que l’énergie cinétique d’une masse « m » se déplaçant à la vitesse « v »
possède une énergie cinétique égale à « EC = (m/2)v2 ».
Lorsque la vitesse initiale de la masse n’est pas nulle, elle a une énergie cinétique initiale égale à
« Eci = (m/2)vi2 » et on voit ainsi que le résultat général obtenu plus haut « W = (m/2)(vf2-vi2) »
exprime tout simplement que l’accroissement d’énergie cinétique vaut le travail appliqué à la
masse, soit « W = ΔEC ».
Ce qui est bien sûr conforme au principe de conservation de l’énergie.
Le théorème de l’énergie cinétique est précieux dans la mesure où il fournit une relation liant les
grandeurs physiques en jeu dans les systèmes mécaniques.
A titre d’exemple, on peut calculer la vitesse acquise depuis le repos (« vi=0 ») par une masse
recevant une énergie sous forme de travail « W », on trouve que cette vitesse vaut la racine de
« 2W/m ».
L’intérêt du théorème de l’énergie cinétique sera illustré au cours des séances d’exercices.
32
On peut encore questionner le principe de conservation de l’énergie avec l’expérience illustrée
ci-dessus. Ce schéma est celui utilisé plus haut pour introduire la notion de travail. Lever le poids
« P » de la hauteur « H » demande une énergie « W = P.H ». Dans cette situation le travail ne
conduit pas à une mise en vitesse de la masse puisque celle-ci est arrêtée une fois le travail
fourni. L’énergie cinétique de la masse est donc nulle et il est légitime de se demander où est
passée l’énergie fournie. Est-elle perdue? Si non quelle forme prend-elle?
Il suffit, par la pensée que l’on déséquilibre la masse pour la faire tomber et on comprend vite
qu’effectivement l’énergie n’est pas perdue car en tombant la masse acquière de la vitesse et
peut même faire des dégâts (si on la reçoit sur le pied par exemple, on réalise très bien que
l’énergie que l’on a donné à la masse n’était effectivement pas perdue).
Pour exprimer le principe de conservation de l’énergie dans les situations de ce type on introduit
la notion d’énergie potentielle. Il s’agit d’une forme d’énergie très abstraite que l’on définit
artificiellement en imposant le principe de conservation de l’énergie. On admet simplement « par
principe », que lorsqu’on lève une masse dans le champ gravitationnel terrestre on accumule de
l’énergie que l’on pourra retrouver en faisant redescendre la masse. Une vision acceptable de ce
principe se trouve dans l’idée que toute force apparaît en couple de forces opposées. Dans le cas
présent le poids « P » est la force exercée par la terre sur la masse. Lorsque la masse n’est pas
retenue et descend, cette force fournit un travail « W=P.Δx = P.H » positif et conduit à une
certaine énergie cinétique (due à la vitesse de chute). Lorsqu’on lève la masse notre force
musculaire fournit un travail positif « W=F. Δx = F.H » alors que la force gravitationnelle
engendre un travail négatif (sens du déplacement opposé à celui de la force), ce qui se traduit
par l’égalité « F = - P ». Les deux travaux sont donc égaux en valeur absolue mais opposés, ils se
compensent donc exactement: il y a conservation de l’énergie.
33
C’est un principe qui est utilisé dans les centrales hydroélectriques.
34
L’eau monte dans le champ gravitationnel terrestre grâce à un barrage et l’énergie accumulée
peut être récupérée sous forme d’énergie cinétique grâce à une turbine qui transforme cette
énergie cinétique en travail dans les générateurs électriques.
35
Le même principe peut s’appliquer à la force électrique. On parle dans ce cas d’énergie
potentielle électrique.
36
La pile électrique est l’illustration la plus évidente de l’énergie potentielle électrique.
La réaction chimique qu’il y a au sein de la pile provoque une séparation des charges électriques
opposées que représentent les protons et les électrons.
De la même manière que notre force musculaire éloigne une masse de la surface de la terre pour
gagner de l’énergie potentielle gravitationnelle, la réaction chimique place les électrons loin des
protons pour leur donner de l’énergie potentielle électrique.
Quand on relie les pôles de la pile par un fil électrique les électrons peuvent y circuler et ils sont
donc libérés de la pile et tombent dans le potentiel électrique exactement comme une masse
tombe dans le potentiel gravitationnel quand on lui en laisse la possibilité.
Cela résulte en pratique en l’apparition d’un courant électrique.
37
Reste maintenant à voir la représentation mathématique de l’énergie potentielle.
Nous avons déjà vu celle du travail et de l’énergie cinétique.
Pour l’énergie potentielle le problème est extrêmement simple dans la mesure où l’énergie
potentielle acquise lors d’un déplacement est, comme on vient de le voir, égale au travail fourni
pour ce déplacement (c’est l’expression du principe de conservation de l’énergie).
On peut donc dire que l’énergie potentielle acquise entre deux coordonnées « xi » et « xf » est
égale à l’intégrale du travail.
Le schéma ci-dessus illustre ce point de vue avec la force gravitationnelle « mg » exercée sur une
masse « m ».
Pour monter cette masse il faut exercer une force « F » égale en valeur absolue mais opposée, il
s’agit donc de la force « F = mg » dirigée vers le haut, comme l’est l’axe des « x » repérant la
hauteur de la masse (la force appliquée à la masse est donc ici positive alors que le poids en
termes de force vectorielle a bien un signe négatif « -mg ».
Cette force étant constante, l’intégrale du travail est simple à calculer et donne « W = mg(xf - xi) ».
Le principe de conservation de l’énergie nous dit que ce travail n’est pas perdu et s’est en réalité
transformé en énergie potentielle.
38
Autrement dit on peut dire que le travail « W = mg(xf - xi) » a résulté en un accroissement
d’énergie potentielle « ΔEP ».
L’expression mathématique de cet accroissement est donc « ΔEP = mg(xf - xi) ».
On peut alors introduire la notion de fonction « énergie potentielle » EP(x) en exprimant, comme
on le fait pour l’accroissement de n’importe quelle grandeur physique, que l’accroissement
d’énergie potentielle entre les points « xi » et « xf » est par définition « ΔEP = EP(xf ) - EP(xi) ».
Si on veut que cette dernière relation soit cohérente avec l’expression de l’accroissement
« ΔEP = mg(xf - xi) », il nous apparaît évident que la fonction énergie potentielle est donnée par
« EP(x) = mgx + cste » où « cste » est une constante quelconque dont on a le choix.
Ce choix est arbitraire mais il est évident qu’en pratique on fait un choix de constante qui rend
les calculs plus simples et plus intuitifs.
Par exemple pour le présent problème de la masse qui s’élève, on peut choisir une constante
nulle de sorte que l’énergie potentielle soit égale à zéro en « x =0 ».
Dans ce cas « x = 0 » représente par exemple le niveau du sol, ou le niveau de la table sur laquelle
on fait des expériences de mécanique avec la masse.
Dans ces conditions on peut écrire la fonction « énergie potentielle » comme suit: « EP(x) = mgx ».
Son graphe est donné en bas à droite.
Remarquez que le fait que l’énergie potentielle soit donnée à une constante près n’est pas un
problème en pratique car dans l’application du principe de conservation de l’énergie, c’est
toujours une différence d’énergie potentielle qui apparaît et la constante disparaît donc toujours
dans la soustraction que cette différence implique.
Remarquez également que la dérivée de la fonction énergie potentielle est égale à la fonction
force (qui est ici la constante « mg »), ce qui est évident dans la mesure où l’énergie potentielle
est obtenue par intégration de la force (intégrale du travail).
39
Le schéma ici montre que la fonction énergie potentielle indique pour une masse donnée « m » la
quantité d’énergie qu’il faut pour la lever jusqu’à la hauteur « x ».
Pour une masse « m » d’un kilo et en admettant que l’accélération « g » de la gravitation terrestre
vaut 10 m/s2, on calcule facilement que tous les mètres l’énergie potentielle augmente de 10
Joules.
40
Si on veut l’expression mathématique de l’énergie potentielle en fonction de la position « x » il
suffit de faire l’intégrale de la force depuis un point de référence (souvent pris comme étant
l’origine) jusqu’à la position « x ».
Le développement ci-dessus donne l’expression de l’énergie potentielle d’un ressort dont la force
est proportionnelle au déplacement « x » (en réalité il faudrait écrire « x – xi » mais on prend ici
« xi = 0 » pour des raisons évidentes de simplicité), soit « F = kx ».
L’intégrale de la force entre 0 et « x » donne donc l’expression de l’énergie potentielle en fonction
de la position « x » atteinte avec l’extrémité du ressort: « EP(x)= (k/2)x2 ».
41
Les graphes de gauche ci-dessus donnent l’interprétation géométrique de l’intégrale de la force.
Il s’agit de l’aire sous la courbe de la force.
Puisque, à l’abscisse « x » correspond l’ordonnée « kx », il apparaît effectivement évident que
l’aire sous la courbe de la force vaut « (k/2)x2 » (la demi surface du rectangle de côtés « x » et
« kx »).
La notion d’énergie potentielle sera approfondie en séance d’exercices.