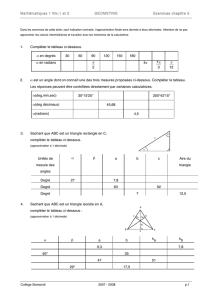
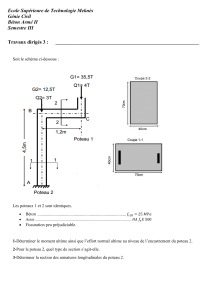
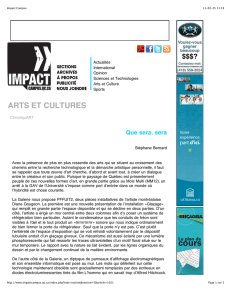
3π 8 2π 5 - Collège Sismondi

Mathématiques 2 Niv.1 et 2 GEOMETRIE Exercices chapitre 1
Collège Sismondi 2008 - 2009 p.1
1. Sachant que ABC est un triangle rectangle en C,
compléter le tableau ci-dessous.
c
!
"
α
(en radian)
β
(en radian)
a
(en cm)
b
(en cm)
c
(en cm)
Aire du triangle
0,7
480
3!
8
26,3
13,4
20
2. Sachant que ABC est un triangle isocèle en A,
compléter le tableau ci-dessous :
A
BC
a
bc
ha
hbhc
α
(en radian)
β
(en radian)
a
(en cm)
b
(en cm)
ha
(en cm)
Hb
(en cm)
2!
5
rad
5,6
0,663 rad
23,4
3. Résoudre les triangles suivants :
a) a = 70,24 b = 82,12 γ = 30,69° b) a = 20,46 β = 58,25° γ = 39,38°
c) a = 41,94 b = 96,92 c = 107,26 d) a = 98,06 b = 364,04 β = 30,65°
e) a = 57,89 b = 10,48 γ= 128,51° f) a = 85,67 β = 123,18° γ = 24,54°
g) a = 60,44 b = 93,83 c = 37,85 h) a = 460,14 b = 335,59 β = 39,37°
i) a = 85,80 c = 57,29 β = 117,81° j) c = 78,54 α = 67,66° β = 85,93°
k) a = 68,87 b = 35,57 c = 81,46 l) a = 345,45 b= 229,14 β = 15,48°
4. Dans lʼexercice ci-dessus, dire dans quel(s) cas, il est possible d'avoir deux solutions différentes.
5. Soit un triangle ABC rectangle en C. Un angle mesure 50° et la surface 60 m2.
Quelles sont les longueurs des côtés de ce triangle ?

Mathématiques 2 Niv.1 et 2 GEOMETRIE Exercices chapitre 1
Collège Sismondi 2008 - 2009 p.2
6. Un géomètre mesure une tour à l'aide d'un
théodolite placé à 1,60 m du sol et à 25 m du
pied de la tour. Il lit un angle de 32°.
Quelle est la hauteur de la tour ?
25 m
1,60 m
32°
Source de lʼimage : Wikipedia
7. Un projecteur dirigé vers un mur situé à 8 m de distance, y dessine un disque lumineux de 12,56 m2.
Quel est l'angle d'ouverture du projecteur?
8. Les faces latérales de cette pyramide sont des triangles équilatéraux
dont les côtés mesurent 10 m.
Quelle est la hauteur de la pyramide ? Quelle est la mesure de l'angle
que fait une face avec le plan horizontal ?
9. On veut connaître la distance qui sépare un point C
d'un point A et d'un point B distant de 300 [m|. On ne
peut pas mesurer cette distance directement, car une
rivière sépare les points A et B d'une part et C d'autre
part. On prolonge la droite CA jusqu'à un point D
distant de 175 m (cʼest-à-dire
!
AD
= 175) et on
mesure
!
BD
= 326 [m], puis on prolonge CB jusqu'au
point E et on mesure
!
BE
= 225 [m]. De plus,
!
DE
= 488 [m].
Calculer
!
AC
et
!
CB
.
A
B
E
D
C
Les exercices10 à 15 sont tirés de Trigonométrie, de Swokowski et Cole
10. Lorsque lʼangle dʼélévation du soleil est de 64°,
un poteau téléphonique qui penche dʼun angle
de 9° par rapport à une ligne formée par le pied
du poteau et le soleil projette une ombre de
6,3 m sur le sol. Calculer la longueur du poteau.
9°
64°

Mathématiques 2 Niv.1 et 2 GEOMETRIE Exercices chapitre 1
Collège Sismondi 2008 - 2009 p.3
11. Un téléphérique transporte des passagers dʼun
point A, qui se trouve à 2 km du point B situé au
pied de la montagne Les angles dʼélévation de P
aux points A et B sont respectivement de 21° et
65°.
a) Calculer la distance entre A et P.
b) Calculer la hauteur de la montagne.
P
21° 65°
A B
12. Les angles dʼélévation dʼun ballon à partir de
deux points au sol A et B distants de 8,4 km
sont respectivement de 24°10ʼ et 47°40ʼ.
Sachant que le ballon se trouve entre les deux
points, dans le même plan vertical, déterminer
lʼaltitude du ballon.
24°10ʼ 47°40ʼ
A B
13. Une route rectiligne forme un angle de 22° avec
lʼhorizontale. Observé dʼun point P sur la route,
lʼangle dʼélévation dʼun avion situé au point A est
de 57°. Au même moment, vu dʼun autre point Q,
situé 100 m plus loin sur la route (cʼest-à-dire
!
PQ
= 100), lʼangle dʼélévation est de 63°.
Sachant que les points P, Q et A sont dans un
même plan vertical, calculer la distance séparant
le point P de lʼavion.
A
P Q
22°
(Rappel : lʼangle dʼélévation se mesure par rapport à lʼhorizontale)
14. Un parallélogramme a des côtés de 30 cm et de 70 cm et un angle de 65°.
Calculer la longueur de chaque diagonale au cm près.
15. Un poteau haut de 10 m est planté sur le flanc
dʼune colline qui forme un angle de 17° avec
lʼhorizontale.
Calculer la longueur minimale dʼun câble tendu
entre le sommet du poteau et un point en
contrebas distant de 21,6 m de la base du
poteau.
C
D
A
B
1
7
°

Mathématiques 2 Niv.1 et 2 GEOMETRIE Exercices chapitre 1
Collège Sismondi 2008 - 2009 p.4
16. L'angle d'ouverture d'un cône circulaire de révolution (par exemple un cône de circulation) mesure 30°
et sa hauteur est de 14,95 [cm]. Calculer le rayon de la base du cône.
17. Une corde sous-tendant un arc de cercle de 82° est à 20 [cm] du centre. Quelle est la longueur de cette
corde ?
18. ABCD est un parallélogramme, sa hauteur
mesure 3 3 ;
α = 60° et
!
AB
= 8
Calculer :
!
AD
,
!
AC
,
!
BD
et l'angle ω.
AB
C
D
h
!
"
19, LEO A L'OEIL SUR OLGA !
O
E
ILG
A
40
24
LEO est un triangle rectangle
OLGA est un losange et
OEIL est un parallélogramme.
A vue d'oeil, lequel est le plus grand : LE ou
LA ?
Et en réalité ?
20. Un champ triangulaire a des côtés de longueurs a, b et c (en mètres). Calculer l'aire du champ sachant
que a = 115, b = 140 et c =200.
21. Un petit jardin en forme de parallélogramme a des côtés mesurant a et b (en mètres) et un des angles
intérieurs mesurant θ.
Calculer l'aire de ce jardin sachant que a = 12, b = 16 et θ = 40°.
22. Pour déterminer la distance séparant deux points A et B, un géomètre choisit un point C qui se situe à
375 m de A et à 530 m de B. Sachant que l'angle BAC mesure 49°30', calculer la distance entre A et B.
23. A l'origine, la tour de Pise était perpendiculaire à la surface du sol et mesurait 54 m de haut. Un côté
s'enfonçant dans le sol, elle penche maintenant d'un angle θ par rapport à la verticale. Lorsque le
sommet de la tour est observé à partir d'un point distant de 45 m du centre de la base, l'angle
d'élévation est de 54,3°.
a) Calculer l'angle .
b) Calculer la distance δ exprimant de combien le centre du sommet de la tour s'est éloigné de la
verticale.
24. Deux voitures quittent une ville en même temps et suivent chacune une autoroute rectiligne, dont les
directions diffèrent de 84°. Si les vitesses des deux voitures sont respectivement de 90 km/h et de 72
km/h, calculer la distance séparant les deux véhicules au bout de 20 minutes.