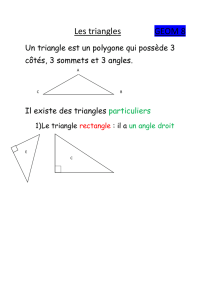
Géométrique, un sens et une intuition à développer (article 3)

Géométrique, un sens et une intuition à développer (article 3)
Robert Lacroix, Séminaire Salésien, Sherbrooke
[email protected]
ENVOL no 142 — janvier-février-mars 2008 43
GRMS
Dernièrement, j’étais proche de la porte d’entrée d’un res-
taurant et j’observais des poissons nager dans un aqua-
rium. Lorsque les poissons étaient dans une partie de
l’aquarium, ils m’apparaissaient plus gros, alors qu’en
d’autres parties, ils étaient plus petits que lorsqu’ils pas-
saient directement devant moi. Ainsi, je sais que, selon
l’emplacement des poissons dans l’aquarium, ils vont
m’apparaître de grosseurs différentes : je le sais parce que
je l’ai vu!
À un autre moment, je me trouve devant mon poêle à
l’huile, il dégage une bonne chaleur en cette journée de
tempête (dimanche 16 décembre 2007). Dans mes mains,
je tiens une tige de métal. M’éloignant du poêle tout en
tenant la tige, je ne suis pas sans penser (c’était assez fa-
cile puisque l’article était en gestation) qu’en éloignant la
tige de métal du poêle, elle se rétrécit. Je sais que les dif-
férences des températures font varier les dimensions des
objets : je le sais parce que je l’ai déjà mesuré. De plus,
les variations des dimensions dépendent des matériaux
qui constituent un objet.
Mais vous allez me dire que, pour l’aquarium, les défor-
mations ne sont qu’apparentes, alors que pour la tige de
métal, la dilatation (contraction) est négligeable. Ah oui?
Si c’est négligeable alors pourquoi les séparations des
rails de chemin de fer? Pourquoi mettre tant d’espace en-
tre les morceaux du tablier d’un pont?
Imaginons qu’à l’époque des grands géomètres, on se soit
aperçu qu’en déplaçant une tige de métal, elle changeait
de longueur, et si l’atmosphère avait été très stratiée et
sachant que la réfringence varie fortement d’une strate
à l’autre, variation tellement prononcée que les objets
auraient semblé changer de forme en les tournant autour
d’un point, aurait-on postulé l’existence des isométries?
Farfelues de telles questions? Ces questions ont déjà été
soulevées par le grand mathématicien français Henri Poin-
caré (dans son livre, Science et hypothèse, paru quelque
temps avant sa mort).
Ces quelques réexions m’amènent à me poser la question
suivante : quels arguments puis-je fournir qui me permet-
tent d’afrmer que toute translation est une isométrie, que
toutes les translations se font suivant la façon enseignée
en géométrie?
Comment puis-je entendre l’afrmation, sans trop sour-
ciller, qu’en faisant tourner un objet dans l’espace, l’objet
ne change pas de forme et il garde ses dimensions?
À propos des rotations : comment prouver que, si je fais
tourner une droite d’un angle q autour d’un point O situé
hors de cette droite, l’image que j’obtiens est une droite et
que cette image forme un angle q avec la droite objet?
« Ben voyons donc » tout le monde sait ça!
– Ah oui?
– Bien, c’est évident!
– Si c’est si évident, on devrait avoir les arguments pour
le prouver. Je me souviens avoir déjà eu des stagiaires in-
capables de le prouver.
– Alors, c’est quoi ta preuve?
– C’est ce que nous allons voir bientôt.
J’ai encore une autre question : « Quels sont les arguments
que je peux fournir pour prouver que les gures sembla-
bles existent (bref, que les homothéties existent)? »
D’autres questions me trottent dans l’esprit comme :
Comment puis-je être si certain que les hauteurs d’un
triangle se rencontrent en un même point? Ce fait avait
émerveillé Einstein quand il était jeune (12 ans) et, quand
il avait acquis la certitude que c’était vrai, il en a été bou-
leversé. Commença alors sa quête ou sa recherche de la
vérité, soupçonnant que la nature recèle une beauté in-
soupçonnée et qu’elle se laisse découvrir petit à petit
par...
Mais par quoi au juste? Et quelle était cette certitude?

ENVOL no 142 — janvier-février-mars 2008
44 GRMS
Qu’est-ce qui me fait dire, hors de tout doute raisonna-
ble, que la somme des angles d’un triangle donne toujours
180˚, quelle que soit sa forme et quelle que soit sa gros-
seur?
Lorsque j’ai commencé cette série d’articles sur la géo-
métrie, je comptais présenter des démonstrations de théo-
rèmes. Mais avec le temps, j’ai craint d’obtenir une litanie
de théorèmes avec leur démonstration; de faire fuir plus
d’un lecteur et plus d’une lectrice. Enn, dans ce qui suit,
je tente une présentation harmonieuse de théorèmes et de
problèmes à résoudre.
D’où, chères lectrices et lecteurs, je vous convie à résou-
dre les quelques problèmes qui émailleront la présenta-
tion.
Sans plus tarder, en voici quelques-uns.
Problème no 1 (de mon bon ami Christian Boissinotte)
Démontrer, que dans un triangle quelconque, le produit
des longueurs de deux côtés est égal au produit du diamè-
tre du cercle circonscrit par la distance séparant le troi-
sième côté et le sommet opposé à ce côté. (À l’aide de la
trigonométrie, ça se fait assez bien, une deuxième solu-
tion est alors requise à l’aide uniquement de théorèmes de
la géométrie, critère imposé par Christian)
Problème no 2
EAB
DCF
G
H
p
q
s
t
u
La gure ci-dessus nous montre un trapèze ABCD dont
les diagonales se rencontrent au point H et que les bases
ont pour longueurs p et q. On prolonge la grande base
BA
jusqu’au point E d’une longueur q et la petite base
DC
jusqu’au point F d’une longueur p. On trace le segment
EF
qui coupe la diagonale
AC
au point G. Les longueurs
des segments
AG
,
GH
et
HC
mesurent respectivement s,
t et u. Montrer que s = u.
D’autres petits problèmes suivront après la présentation
d’un peu de théorie.
Que verrons-nous dans cet article?
Dans cet article, nous ne pourrons pas aborder les répon-
ses à toutes les questions posées an d’avoir un article
d’une longueur raisonnable.
Dans cet article donc, j’aborderai les rotations et les trian-
gles semblables pour lesquels je trouve qu’on prend pour
acquis leurs propriétés, et je rappelerai quelques proprié-
tés des proportions.
Mais avant de regarder les rotations, jetons un regard sur
un théorème fondamental en géométrie : celui portant sur
la somme des angles intérieurs d’un triangle.
Un des plus grands théorèmes de la géométrie est celui
traitant de la somme des angles intérieurs d’un triangle.
Nous sommes tellement habitués de le rencontrer, qu’il
nous apparaît banal. Pourtant, il est à la base de la géomé-
trie d’Euclide et de la trigonométrie.
Examinons quelques preuves :
Preuve no 1
AB
C
D
Considérons un rectangle ABCD. La somme des angles
intérieurs est manifestement égale à 360˚. Si je trace la
diagonale
AC
, je partage le rectangle en deux triangles
rectangles qui ont exactement les mêmes mesures.
Ainsi, la somme des angles à l’intérieur d’un triangle
rectangle
360 180
2
= =
.
La preuve se poursuit sur l’autre page.

ENVOL no 142 — janvier-février-mars 2008 45
GRMS
C
AB
H
Traçons maintenant un triangle ABC et traçons
CH
, la
hauteur issue du sommet C. Ainsi, dans chacun des trian-
gles rectangles, la somme des angles = 180˚ pour un total
de 360˚. Maintenant, les angles formés au pied de la hau-
teur
AH
totalisent 180˚; ainsi, la somme des angles du
triangle ABC donne 180˚
Preuve no 2
AB
C
D
180° - B
180° - C
180° - A
Considérons un triangle ABC tel que dessiné dans la -
gure laissant voir les angles extérieurs au triangle. Main-
tenant, en partant du point D(épart) sur le côté
AB
, mar-
chons autour du triangle en suivant le èche pour revenir
au point D. En chacun des sommets rencontrés, (B, C, A)
il a fallu tourner de trois angles : 180˚- B, 180˚ - C et 180˚-
A pour partir et revenir au point D. On a donc tourné d’un
total 540˚ - (A + B + C), ce qui aurait donné le même effet
que de tourner sur place de 360˚ sans se déplacer. Ainsi,
A + B + C = 180˚.
Preuve no 3
AB
C
D
E
xx
y
z
z
La preuve classique est de tracer par un des sommets une
parallèle au côté opposé.
Sur la gure, nous avons tracé
DE
parallèlement au côté
AC
.
Soit x, y et z les mesures des angles intérieurs du triangle
ABC.
Par les propriétés des mesures des angles alternes-internes
déterminés par une sécante à deux droites parallèles, les
mesures x et z sont aussi celles des angles ABD et EBC.
Donc x + y + z = 180˚.
Seule cette dernière preuve a résisté aux critiques des
mathématiciens (je devrais dire géomètres) au cours des
deux derniers millénaires.
« Tournons » notre regard sur les rotations
Plusieurs afrmations sont formulées sur les rotations :
une rotation préserve les longueurs, une rotation préserve
les angles d’une gure, l’angle entre une droite et son
image par une rotation est une droite, etc. Ces afrmations
sont formulées dans des livres, mais sans être prouvées.
Dans ce qui suit, nous fournissons quelques preuves sim-
ples.
A
A' B
B'
C
C'
q
O
Pour étudier l’image de la rotation d’une droite autour
d’un point O d’un angle q, choisissons 3 points quelcon-
ques A, B et C sur cette droite. Soit A', B' et C' les images
de ces points par cette rotation.
Sur la gure, nous ne montrons qu’un seul arc cercle
AA'
pour illustrer le plus complètement la rotation du point A
d’un angle q autour du point O. Par cette construction :

ENVOL no 142 — janvier-février-mars 2008
46 GRMS
OA
=
OA'
de même on peut afrmer que
OB
=
OB'
et
OC
=
OC'
; de plus, les angles BOB' et COC' sont égaux à q.
Il nous faut montrer que les points A', B' et C' sont coli-
néaires et que la droite
A'B'
fait un angle q avec la droite
AB
.
A
A' B
B'
C
C'
q
O
α
α
Montrons que les segments
AB
et
A'B'
ont même lon-
gueur.
Pour cela, montrons que les triangles AOB et A'OB' sont
congrus par le postulat CAC.
À cette n, il faut montrer que les angles AOB et A'OB'
ont même mesure.
On sait que
AOB' B'OB AOB∠ − ∠ = ∠
AOB' AOA' A'OB'∠ − ∠ = ∠
B'OB AOA' q∠ = ∠ =
Donc,
AOB A'OB'∠ = ∠
Comme
OA
=
OA'
et
OB
=
OB'
alors les triangles AOB et
A'OB' sont congrus d’où
AB
=
A'B'
.
Par une suite d’arguments similaires, on prouve que
BC
=
B'C'
; et que
AC
=
A'C'
.
Puisque les points A, B et C sont colinéaires :
AB
+
BC
=
AC
=
A'B'
+
B'C'
=
A'C'
.
Ainsi, les points A', B' et C' sont colinéaires en vertu du
théorème sur l’inégalité du triangle.
Il nous reste à prouver que l’angle entre les droites
AB
et
A'B'
est q, la mesure de l’angle de rotation.
Soit I, le point d’intersection des droites
AB
et
A'B'
.
Montrons que
B'IB = q∠
.
Soit
= OAB = OA'B'a∠ ∠
α.
Dans le quadrilatère OAIA’, la somme des angles = 360˚ :
OAB + AOA' + OA'I + A'IA = 360°∠ ∠ ∠ ∠
d’où
+ + 180° - + 180° - B'IB = 360°qa a ∠
α
α.
D’où on tire aisément que
B'IB = q∠
.
Problème no 3
gure 3.0 gure 3.1 gure 3.2
gure 3.4gure 3.3
La suite des gures 3.0 à 3.4 illustre le fait suivant : nous
commençons par tracer un triangle équilatéral, gure 3.0;
à l’intérieur de ce triangle, nous découpons un triangle
équilatéral (triangle en foncé) formant ainsi un trou dans
le centre du premier triangle; les sommets du triangle
troué se situent aux milieux des côtés du premier triangle.
Nous répétons cette procédure pour chaque triangle équi-
latéral blanc apparaissant dans la gure 3.1 pour obtenir
la gure 3.2.
De la gure 3.2, nous pouvons obtenir la gure 3.3 qui,
lorsque trouée de la même manière, nous donne la gure 3.4.
Considérons les triangles blancs. Si nous nous étions ren-
dus à la gure 3.5 en partant de la gure 3.4, déterminer le
rapport entre l’aire totale des triangles blancs et l’aire du
I

ENVOL no 142 — janvier-février-mars 2008 47
GRMS
triangle de la gure 3.0. et déterminer le rapport entre la
somme des périmètres des triangles blancs et le périmètre
du triangle initial.
Regard sur les triangles semblables
L’intuition de l’existence des gures semblables vient du
fait qu’on peut concevoir des objets qui se ressemblent
tout en ayant des grosseurs différentes.
L’histoire raconte que Thales de Milet (-650) aurait pu dé-
terminer la hauteur de la Grande Pyramide en comparant
la longueur de son ombre projetée au sol avec l’ombre de
la Grande Pyramide.
Dans ce qui suit, je vais esquisser une démarche logique
qui amène aux triangles semblables et donc, à la notion
d’homothétie.
Pour commencer, voyons la gure suivante :
AA'
B B'
C'
C
Trois droites parallèles AA', BB' et CC' sont coupées par
deux sécantes AC et A'C'.
Nous avons appris l’existence de la proportion suivante :
s.1)
AB A'B'
=
BC B'C'
et que de cette proportion on tire la proportion qui suit :
s.2)
AB A'B'
=
AC A'C'
Deux questions sont soulevées : comment prouver la pre-
mière proportion? Et, d’où vient la deuxième?
Certains diront, comme je l’ai déjà entendu, que la pre-
mière vient des triangles semblables qui sont formés en
prolongeant
CA
et
C'A'
jusqu’à leur point d’intersection.
Sur le plan logique, cette réponse est parfaite. Mais d’où
viennent les propriétés des triangles semblables?
Sans tout rebâtir la géométrie, esquissons une démarche.
La clé réside dans le beau théorème suivant que j’ai l’ha-
bitude d’appeler : théorème milieu-milieu.
Théorème milieu-milieu
AA'
B B'
C'
C
Si trois droites parallèles découpent des segments de
même longueur sur une sécante, alors elles découpent sur
toute autre sécante des segments de même longueur.
Ainsi, si AA', BB' et CC' sont trois droites parallèles et
que B est au milieu de
AC
, alors B' est au milieu de
A'C'
.
La démonstration est assez simple à élaborer :
D
E
AA'
B B'
C'
C
Traçons
AD
et
BE
parallèlement à A'C'.
Nous avons donc 2 triangles congrus sur cette gure par le
postulat ACA. Ainsi, les segments
AD
et
BE
ont la même
longueur. Puisque nous avons aussi deux parallélogram-
mes, alors
AD
=
A'B'
et
BE
=
B'C'
.
Donc
A'B'
et
B'C'
ont la même longueur, d’où B' est au
milieu du segment
A'C'
.