Chapitre 8 : Les angles

Chapitre 8 : Les angles
Ils sont utilisés pour se repérer sur la Terre (GPS), dans les boussoles et en
astronomie, en optique (appareil photo, lunettes), en construction (pente d’une
route), …
1) Vocabulaire et notations :
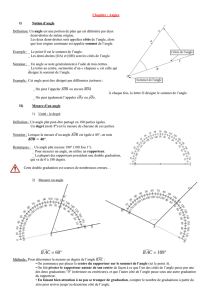
Un angle est formé par deux demi-droites qui ont la même origine.
Le sommet de l’angle est l’origine, les côtés de l’angle sont les demi-droites.
Exemple :
y
On trace un petit arc de cercle entre les deux demi-droites.
Remarque : une demi-droite se note de plusieurs manières donc un angle
aussi :
E BAD = CAD = CAE = … = A
D (le sommet est toujours au milieu).
A
B C
Rappel : sur une demi-droite, les points (B, D, C,…) s’écrivent à côté d’un petit
trait en prolongeant. Les directions (x, y, …) s’écrivent au bord sans trait.
Le sommet de l’angle est le point A.
Les côtés de l’angle sont les demi-
droites [Ax) et [Ay).
A x Cet angle se note xAy ou A.
x
le même angle de plusieurs manières :
O = = BOD = AOC = …
D C O (Le sommet est toujours au milieu)

2) Le rapporteur :
On mesure un angle avec un rapporteur, qui est un demi-cercle partagé en 180
parties égales.
L’unité est le degré, noté ° (comme pour les températures).
Les graduations vont de 0 à 180 degrés.
Souvent, le rapporteur a deux graduations en degrés :
- une graduation sur le demi-cercle extérieur avec le zéro à gauche.
- une autre graduation sur le demi-cercle intérieur avec le zéro à droite.
90°
45°
150°
90°60°
1150° 120° 30°
0° 180 0 180°
centre du rapporteur
Remarque : 30° est en face de 150°. Il ne faut pas les confondre : 30° est plus
petit que 90° qui est la mesure de l’angle droit, 150° est plus grand.

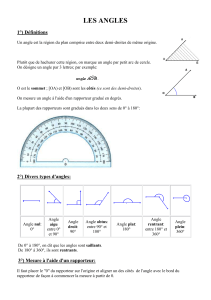
3) Mesurer un angle :
On lit 30° y
A x
La mesure d’un angle est le nombre de degrés entre les deux côtés de l’angle.
Pour mesurer l’angle xAy, on place le centre du rapporteur sur le sommet A de
l’angle. Puis on aligne le zéro d’une graduation (ici, le zéro intérieur situé à
droite) sur un côté de l’angle EN GARDANT LE CENTRE DU RAPPORTEUR sur
le sommet.
On lit alors la mesure de l’angle sur la graduation intérieure alignée avec le
deuxième côté de l’angle.
Remarques :
● Les demi-droites doivent dépasser du rapporteur pour lire la graduation.
Sinon, on les prolonge avec la règle ( même sans tracer si c’est sur un livre).
● On sait AVANT de mesurer si un angle est plus grand ou plus petit que 90° :
y
y
A x B x
angle plus petit que 90° angle plus grand que 90°
(angle aigu) (angle obtus)
● On compte toujours à partir de zéro pour ne pas confondre les deux
graduations et on vérifie que la mesure obtenue correspond bien à l’angle (plus
petit ou plus grand que 90° qui est l’angle droit).
● On tourne sa feuille ou son rapporteur si la première demi-droite n’est pas
horizontale.

4) Construire un angle :
Pour construire un angle xAy de 30°, on commence par tracer une demi-
droite [Ax) d’origine A.
Puis on pose le centre du rapporteur sur le point A en alignant le zéro de l’une
des deux graduations sur la demi-droite.
●
x
A
On repère la graduation 30° à partir de zéro et on trace un point en face de
cette graduation.
On enlève le rapporteur et on trace la demi-droite d’origine A passant par ce
point. On note la direction y sur la figure, on trace un petit arc de cercle
entre les deux demi-droites et on écrit 30° juste à côté.
Remarques :
● On trace un trait le plus long possible et d’au moins 7 cm pour les demi-
droites. Il faut que le trait dépasse du rapporteur pour aligner le zéro de la
graduation.
● Attention encore à ne pas confondre les deux graduations (les angles plus
petits ou plus grands que 90° ne se ressemblent pas ! )
● Attention aussi à ne pas tracer un angle de 48° au lieu de 52°.
(Deux degrés avant ou après 50°). Avec la graduation extérieure, on tourne
vers la droite, avec la graduation intérieure, on tourne vers la gauche.

Annexe : extrait du programme officiel 2016 :
Identifier des angles dans une figure géométrique.
Comparer des angles.
Reproduire un angle donné en utilisant un gabarit.
Reconnaitre qu'un angle est droit, aigu ou obtus.
Estimer la mesure d'un angle.
Estimer et vérifier qu'un angle est droit, aigu ou obtus.
Utiliser un instrument de mesure (le rapporteur) et une unité de mesure (le degré) pour :
- déterminer la mesure en degré d'un angle ;
- construire un angle de mesure donnée en degrés.
- Notion d'angle.
- Lexique associé aux angles : angle droit, aigu, obtus.
- Mesure en degré d'un angle.
Avant le travail sur les mesures, établir des relations entre des angles (sommes, partages, référence aux angles du triangle équilatéral, du
triangle rectangle isocèle).
Comparer des angles sans avoir recours à leur mesure (par superposition, avec un calque).
Différencier angles aigus et angles obtus
Estimer la mesure d'un angle, par exemple à 10° près, et vérifier à l'aide du rapporteur.
Utiliser des gabarits d'angles, l'équerre, le rapporteur. Le rapporteur est un nouvel instrument de mesure qu'il convient d'introduire à
l'occasion de la construction et de l'étude des figures.
Les angles : Au primaire, il s'agit d'estimer et de vérifier, en utilisant l'équerre si nécessaire, qu'un angle est droit, aigu ou obtus, de comparer
les angles d'une figure puis de reproduire un angle, en utilisant un gabarit. Ce travail est poursuivi au collège, où l'on introduira une unité de
mesure des angles et l'utilisation d'un outil de mesure (le rapporteur).