CONTRÔLE N°5 TS LA CALCULATRICE N’EST PAS AUTORISÉE

CONTRÔLE N°5 TS
LA CALCULATRICE N’EST PAS AUTORISÉE
Exercice 1 : Oscillations électriques (circuit RLC)
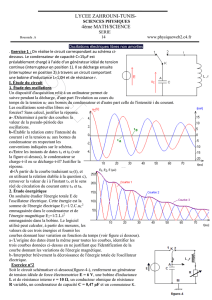
On réalise le circuit correspondant au schéma en dernière page figure 1.
Le condensateur de capacité C = 10 µF est préalablement chargé à l'aide d'un générateur idéal de tension
continue (interrupteur en position 1). Il se décharge ensuite (interrupteur en position 2) à travers un circuit
comportant une bobine d'inductance L et de résistance r.
1. Étude des oscillations
Un dispositif d’acquisition relié à un ordinateur permet de suivre, pendant la décharge, d’une part
l’évolution au cours du temps de la tension u
C
aux bornes du condensateur et d’autre part, celle de
l’intensité i du courant. On obtient la figure 2 de la dernière page.
1.a. Pourquoi parle-t-on d’oscillations libres ? Préciser la nature des oscillations observées.
1.b. Déterminer à partir des courbes la valeur de la pseudo-période des oscillations. La
représenter sur la figure.
1.c. En admettant que l'on peut assimiler cette pseudo-période à la période des oscillations non
amorties du circuit LC correspondant, donner une valeur approchée de l'inductance L de la bobine.
(On prendra π
2
≈ 10)
1.d. Etablir l'équation différentielle à laquelle satisfait la tension u
C
en respectant les conventions
indiquées sur la figure.
1.e. Quelle est la valeur de l'intensité à l'instant t = 0 ? En déduire la valeur de la tension u
L
(t=0)
aux bornes de la bobine. Justifier.
1.f. Établir la relation entre l'intensité du courant i et la tension u
C
aux bornes du condensateur en
respectant les conventions indiquées sur le schéma.
1.g. Entre les instants de dates t
A
et t
B
(voir la figure 2), le condensateur se charge-t-il ou se
décharge-t-il ? Justifier la réponse.
1.h. À partir de la courbe traduisant u
C
(t), et en utilisant la relation entre l'intensité du courant i et
la tension u
C
aux bornes du condensateur (en respectant les conventions indiquées sur le schéma),
retrouver la valeur de i à l'instant t
A
et le sens réel de circulation du courant entre t
A
et t
B
.
2. Modélisation
On considère que la résistance de la bobine est nulle.
2.a. Ecrire la nouvelle équation différentielle à laquelle satisfait u
C
.
2.b. Quelle est l'expression littérale de la période des oscillations qui prennent naissance dans le
circuit ?
2.c. Vérifier que u
C
(t) = U
m
cos(
t
T
2
0
π
) est solution de l'équation différentielle écrite en a.
2.d. En déduire l'expression de la charge du condensateur, puis de l'intensité dans le circuit en
fonction du temps.
3. Étude énergétique
On souhaite étudier l'énergie totale E de l'oscillateur électrique. Cette énergie est la somme de l'énergie
électrique E
1
=
2
1
C.u
2
emmagasinée dans le condensateur et de l'énergie magnétique E
2
=
2
1
L.i
2
emmagasinée dans la bobine. Le logiciel utilisé peut calculer, à partir des mesures, les valeurs de ces trois
énergies et fournir les courbes donnant leur variation en fonction du temps (voir figure 3 en dernière
page).
3.a. L'origine des dates étant la même pour toutes les courbes, identifier les trois courbes données
en figure 3, en ne justifiant que l'identification de la courbe donnant les variations de l'énergie
magnétique.

3.b. Interpréter brièvement la décroissance de l'énergie totale de l'oscillateur électrique.
3.c. On suppose maintenant que l'oscillateur ne comporte aucune résistance. Établir les
expressions:
- de l'énergie électrique en fonction de C, U
m
,T
0
et t;
- de l'énergie magnétique en fonction de C, U
m
,T
0
et t.
Montrer que, dans ce cas, l'énergie totale de l'oscillateur est conservée .
Exercice 2 : Restauration d’un boulet par électrolyse
Un boulet est retrouvé par un archéologue, qui le restaure par électrolyse en solution basique.
Ce procédé a pour but, notamment :
– d’éliminer la gangue (substance qui forme une enveloppe autour d’une autre matière) qui
entoure le boulet ;
– de débarrasser l’objet de tous les ions chlorure qui, au contact de l’humidité de l’air et du
dioxygène amènent à la formation d’acide chlorhydrique conduisant à la destruction rapide du
boulet. Ces ions chlorure sont également présents dans la gangue.
Le schéma de principe de l’électrolyse est représenté figure 4 en dernière page.
La lente destruction de la gangue libère dans l’électrolyte les ions chlorure qu’elle contenait.
L’équation de la réaction modélisant l’électrolyse est : 2 Cl
−(aq)
+ 2H
2
O
(l)
= Cl
2
(g) + H
2(g)
+ 2HO
−(aq)
Les couples d’oxydoréduction mis en jeu sont : Cl
2(g)
/Cl−
(aq)
et H
2
O
(l)
/H
2(g)
.
1. La réaction se produisant à l’anode est-elle une oxydation ou une réduction ?
2. Écrire l’équation de la réaction ayant lieu à l’anode. À quelle borne du générateur est reliée
cette électrode ?
3. À l’une des électrodes, on observe un dégagement de dihydrogène. L’équation de la réaction
électrochimique associée est : 2H
2
O
(l)
+ 2 e− = H
2(g)
+ 2HO
−(aq)
(1)
La pression exercée par le dihydrogène permet de décoller la gangue. L’élimination de la gangue se fait
sous une intensité I constante et pendant une durée ∆t qui dépendent, entre autres, de la nature de l’objet
et de son état de corrosion.
Données :
– Charge élémentaire : e = 1,6 × 10
−19
C;
– constante d’Avogadro : N
A
= 6,0 × 10
23
mol
−1
;
– intensité du courant : I = 1,0 A;
– durée de l’électrolyse : ∆t = 530 heures.
Aide au calcul
5,3 × 3,6 ≈ 19 ; 2 × 1,6 × 6 ≈ 19 ; 6,3
3,5
≈ 1,5 ;
6,1 62
×
= 7,5
On note Q la valeur absolue de la charge électrique totale ayant circulé dans le dispositif pendant la durée
∆t de l’électrolyse.
3.1. Donner l’expression littérale du nombre N d’électrons transférés et celle de la quantité
d’électrons n(e) en fonction des grandeurs données.
3.2. Pour simplifier, on fait l’hypothèse que la réaction correspondant à l’équation (1) est la seule
à se produire au niveau de l’électrode concernée. En s’aidant éventuellement d’un tableau
d’avancement, établir une relation entre la quantité n(H
2
) de dihydrogène dégagé et la quantité
d’électrons n(e) et en déduire que : n(H
2
) =
A
Ne2 tI ××
∆
×
3.3. Calculer la valeur de n(H
2
).
3.4. En déduire quel serait le volume de dihydrogène dégagé dans les conditions de l’expérience.
On donne le volume molaire des gaz dans les conditions de l’expérience : V
m
= 24 L. mol
−1
.

Nom : prénom :
Figure 1
Figure 2
Figure 3
Figure 4