Exo1-ETUDE D`UN DIPOLE RL 4pts

LYCEE ZAHROUNI-TUNIS-
SCIENCES PHYSIQUES
4ème MATH/SCIENCE
SERIE
Boussada .A 14 www.physiqueweb2.c4.fr
Oscillations électriques libres non amorties
. Exercice 1 : On réalise le circuit correspondant au schéma ci-
dessous. Le condensateur de capacité C=15µF est
préalablement chargé à l'aide d'un générateur idéal de tension
continue (interrupteur en position 1). Il se décharge ensuite
(interrupteur en position 2) à travers un circuit comportant
une bobine d'inductance L=1,0H et de résistance r.
I. Étude du circuit
1. Étude des oscillations
Un dispositif d'acquisition relié à un ordinateur permet de
suivre pendant la décharge, d'une part l'évolution au cours du
temps de la tension uC aux bornes du condensateur et d'autre part celle de l'intensité i du courant.
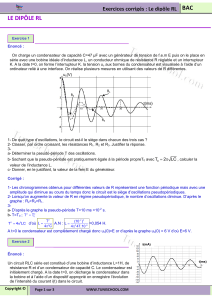
Les oscillations sont-elles libres ou
forcées? Sans calcul, justifier la réponse.
a- /Déterminer à partir des courbes la
valeur de la pseudo-période des
oscillations.
b-/Établir la relation entre l'intensité du
courant i et la tension uC aux bornes du
condensateur en respectant les
conventions indiquées sur le schéma.
c-/Entre les instants de dates tA et tB (voir
la figure ci-dessus), le condensateur se
charge-t-il ou se décharge-t-il? Justifier la
réponse.
d-/À partir de la courbe traduisant uC(t), et
en utilisant la relation établie à la question c),
retrouver la valeur de i à l'instant tA et le sens
réel de circulation du courant entre tA et tB.
2. Étude énergétique
On souhaite étudier l'énergie totale E de
l'oscillateur électrique. Cette énergie est la
somme de l'énergie électrique E1=1/2.C.uC2
emmagasinée dans le condensateur et de
l'énergie magnétique E2=1/2.L.i2
emmagasinée dans la bobine. Le logiciel
utilisé peut calculer, à partir des mesures, les
valeurs de ces trois énergies et fournir les
courbes donnant leur variation en fonction du temps (voir figure ci dessous).
a-/L'origine des dates étant la même pour toutes les courbes, identifier les
trois courbes données ci-dessus en ne justifiant que l'identification de la
courbe donnant les variations de l'énergie magnétique.
b-/Interpréter brièvement la décroissance de l'énergie totale de l'oscillateur
électrique.
Exercice n°2
Soit le circuit schématiser ci-dessous(figure-4-), renferment un générateur
de tension idéale de force électromotrice E = 6 V, une bobine d'inductance
L et de résistance interne r = 10 Ω, un conducteur ohmique de résistance
R variable, un condensateur de capacité C = 0,47 μF et un commutateur K.

A l'aide d'u oscilloscope, on enregistre les variations
de la tension aux bornes du condensateur.
1°) Lorsqu'on ferme le commutateur K sur la position 1, on remarque que la tension uAM s'établit instantanément.
Interpréter ce résultat.
2°) A une date t = 0, on bascule K sur la position 2
a- Quel phénomène se produit dés qu'on ferme K sur la position 2.
b- Etablir dans ce cas l'équation différentielle en uAM.
3°) Pour une certaine valeur de R, on obtient l'enregistrement suivant(fig5)
a- En quel régime fonctionne le circuit?
b- Déterminer la pseudo période T des oscillations du circuit.
c- Sachant que dans les conditions du circuit la pseudo période T peut-être exprimer par la relation:
T = 2π
LC
. Déduire la valeur de l'inductance L de la bobine.
4°) a- Calculer la valeur de l'énergie totale E1 du circuit à la date t1 = 0.
b- Calculer la valeur de l'énergie totale E2 du circuit après trois oscillations.
c- Comparer E1 et E2, conclure.
d- Interpréter cette variation d'énergie.
5°) En supposant que le rapport:
) t-( - 1
L
o
R
e 2
t
1
2=
E
E
avec Ro=R + r. Déduire
la valeur de R
On rappelle que : ln(ex ) = x.
EXERCICE N° 3
On réalise un circuit (RLC) série
comprenant :
- Un condensateur de capacité C
initialement chargé.
- Une bobine d’inductance L = 0,2
H et de résistance négligeable..
- Un résistor de résistance R
variable.
La tension uc aux bornes du condensateur
est observée à l’aide d’un oscilloscope.
1) Pour R =R1 = 10 Ω on obtient
la courbe suivante.
a- Déterminer la pseudo période des
oscillations.
b- Calculer la capacité C du
condensateur si l’on admet que la
pseudo-période est pratiquement
égale à la période propre T0 du
circuit (LC).
c- Etablir l’équation différentielle de
l’oscillateur amorti.
d- Montrer que l’énergie totale de l’oscillateur n’est pas conservée.
e- Evaluer l’énergie thermique dissipée dans le circuit au bout de 4 pseudo périodes.
2) Pour trois valeurs différentes R2, R3 et R4 de R, toutes différentes de 0 et telles que R2 R3 R4 ; on
obtient les courbes suivantes (a) ,(b) et (c).
a- Attribuer à chaque courbe la résistance correspondante. Justifier la réponse.
b- Indiquer dans chaque cas le régime de fonctionnement.
t
u
t
u
t
u
a
b
c
t(ms)
u(V)
0
π
2π
5
Fig 5
t(ms)