devoir 1 (hiver 2014) Alg`ebre moderne appliquée Le devoir est `a

devoir 1 (hiver 2014)
Alg`ebre moderne appliqu´ee
Le devoir est `a remettre au plus tard le 24 f´evrier. Vous pouvez faire le devoir en ´equipe
de 4 ou moins.
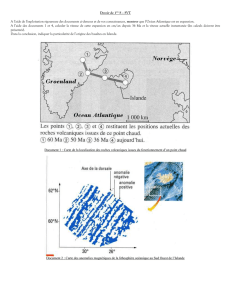
Exercice 1 Consid´erons une portion de la plan`ete Terre de 100 km2que l’on consid`erera
(pour simplifier) comme un plan ayant deux dimensions. Dans ce carr´e on a pla¸c´e 3 sis-
mographes (non-colin´eaires). Ces sismographes peuvent enregistrer les temps de vibration
d’une onde terrestre passant par leur position. On suppose que les sismographes ont des
horloges compl`etement synchronis´ees. Supposons qu’une m´et´eorite frappe le sol au temps
tet que l’onde de choc se d´eplace `a vitesse constante v m/s dans toutes les directions du
plan. Donner une mani`ere de calculer l’endroit exact o`u la m´et´eorite est tomb´ee. (Vous
devez justifier votre r´eponse)
Exercice 2 (exercices 15 et 16 `a la p. 39) On a vu en classe comment-est-ce qu’`a l’aide
d’un GPS il est possible de d´eterminer sa position terrestre. Le but de cet exercice est de
vous montrez qu’il est possible d’utiliser la position du Soleil dans le ciel `a midi (`a certains
moments pr´ecis dans l’ann´ee) afin d’obtenir de l’information sur sa position terrestre. Pour
tout cet exercice, on utilise les coordonn´ees sph´eriques telles que discut´es en classe.
L’axe de la Terre fait un angle de 23.5 degr´es (`a chaque instant) avec la normale au
plan de l’´ecliptique (le plan sur lequel gravite la Terre autour du Soleil)
(1) Le cercle polaire est situ´e `a 66.5 degr´es de latitude nord. Si vous ˆetes au cerlce polaire,
avec quel angle voyez-vous le Soleil au moment de l’´equinoxe? Au solstice d’´et´e? Au
solstice d’hiver? L’angle ici, correspond `a l’angle fait entre le z´enith (la direction
au-dessus de la tˆete) et le Soleil.
(2) Si le Soleil fait un angle θau-dessus de l’horizon `a midi au solstice d’´et´e, calculez
votre latitude?
Exercice 3 (exercice 11, p. 38) Montrer que, si une suite {an}n∈Zest p´eriodique de
p´eriode N, alors sa p´eriode minimale M, `a savoir le plus petit entier Mtel que an+M=an
pour tout n, est n´ecessairement un diviseur de N.
Exercice 4 (exercice 13, p. 38)
(1) Montrer que le polynˆome g(x) = x4+x3+x2+x+ 1 ∈F2[x] est irr´eductible, mais
n’est pas primitif.
(2) Calculer la suite g´en´er´ee par le r´egistre `a d´ecalage si on prend (q0, q1, q2, q3) =
(1,1,1,1) et les conditions initiales
(a0, a1, a2, a3) = (T(β), T (xβ), T (x2β), T (x3β)),
pour β=1∈Fg(x), o`u Fg(x)est le corps fini de cardinalit´e 24et Test la fonction
trace telle que d´efinie dans le livre (voir p. 24).
1

(3) Calculer la p´eriode minimale de la suite g´en´er´ee en (2).
Exercice 5 On consid`ere la sph`ere de rayon 1 et centr´ee en (0,0,0) dans R3. Donner
un formule explicite pour l’aire de la sph`ere comprise entre les valeurs de z,a≤z≤bpour
des valeurs de aet bcomprisent −1≤a≤b≤1.
Exercice 6 (exercice p. 40) Sur une carte obtenue par projection de Mercator, calculer
l’´equation de l’orthodromie joingant le point de longitude 0 et latitude 0 avec le point de
longitude 90 degr´es ouest et de la latitude 60 degr´es nord.
2