Leçon 01/p.14à17/XP

CALCUL MENTAL
cCalcul réfléchi b
Arrondis les nombres suivants
à la centaine la plus proche :
495 ; 862 ; 1 639 ; 2 485 ;
13 423 ; 15 000 ; 19 307.
Exemple :
495 ➤500
400 ➤495 – 95
500 ➤495 + 5
5 < 95
Arrondis les nombres suivants
au millier le plus proche :
8 748 ; 8 095 ; 6 772 ; 6 277 ;
94 618 ; 53 235 ; 572 824.
Exemple :
8 748 ➤9 000
8 000 ➤8 748 – 748
9000 ➤8748 + 252
252 < 748
AU CŒUR DES DOCUMENTS
•Les grands nombres se lisent
en regroupant leurs chiffres
par classe : milliards, millions,
milliers et unités.
•Dans un nombre écrit
en chiffres, on utilise zéro
pour signifier l’absence
d’unités, de dizaines,
de centaines de chaque
classe.
15
DOCUMENT
❶ Quelle est la température de l’Univers
après sa naissance ?
Écris ce nombre en chiffres.
DOCUMENT
❶Écris les nombres du tableau de la
superficie en lettres.
❷Écris les nombres de la population
en unités de milliers.
Exemple : 798 000 ou 798 milliers.
DOCUMENT
❶Combien de téléspectateurs du
monde (hors Amérique) assisteront
à ce XXXIIESuperbowl ?
Écris ce nombre en chiffres.
❷Combien d’Américains regardent
la finale de cette compétition ?
Écris ce nombre en lettres.
C
B
A
Quel curieux !
Les grands nombres
POUR RÉPONDRE
AUX QUESTIONS
Il n’y a aucun calcul à faire.
Il faut juste savoir lire les données.
Pour cela, tu peux utiliser
un tableau de numération.
24 240 600 se lit :
vingt-quatre millions deux cent
quarante mille six cents.
Pour bien lire un grand nombre,
groupe ces chiffres par trois
à partir de l’unité de la classe
des unités.
AU CŒUR DE LA NOUVELLE POUR ALLER PLUS LOIN
•Écrire les grands nombres
en chiffres et en lettres.
•Distinguer chiffre et nombre.
14
❶D’après Laura, quel est le nombre
exact de villages en Inde ?
Comment faire pour lire ce nombre ?
❷Fais la même recherche avec le
nombre d’habitants.
❸S’il y avait deux dizaines de milliers
d’habitants supplémentaires, quelle
serait la population de l’Inde ?
Écris ce nombre en chiffres et en
lettres.
❶Écris en lettres les deux nombres uti-
lisés par Laura : nombre de villages,
nombre d’habitants.
❷Écris les deux nombres de la nouvelle
de deux façons différentes :
– exprimés en centaines ;
– exprimés en centaines de milliers.
Julien ouvre la boîte aux lettres.
« Tiens ! Une carte pour Roxane… »
Curieux, il regarde de plus près.
Le timbre indique qu’elle vient
d’Inde et elle est signée d’une
camarade de classe partie
en vacances avec ses parents.
Il lit :
« Chère Roxane,
Nous avons fait un excellent
voyage. Ici, il fait très chaud,
jusqu’à 47 °C, et c’est la période de
la mousson. L’Inde est un très grand
pays qui comporte 600000 villages
pour 987000000 d’habitants. Cela
fait du monde !… Je t’embrasse.
Laura. »
« Roxane ? ! Tu as du courrier ! »
La petite fille saute de joie.
« Chouette ! Une carte de Laura ! »
Et elle se plonge dans la lecture.
« Tu te rends compte !… s’exclame-
t-elle en direction de Julien. En Inde,
il y a des centaines et des centaines
de villages. »
Et elle tente de relire le nombre
écrit par Laura, mais n’y arrive pas
précisément.
« Mais non ! renchérit Julien.
C’est beaucoup plus ! Elle te dit
qu’il y a des milliers et des milliers
de villages !
– Quoi ! s’étonne Roxane. Comment
le sais-tu ? Tu as lu ma carte ?…
Tu as osé ?… » ■
classe des
millions
classe des
milliers
c d u c d
2 4 2 4 0
u
6
c
0
d
0
u
POPULATION
POPULATION
EN 1999
FRANCE métropolitaine 58 518 000
Région PACA 4 506 000
Département des Bouches-du-Rhône 1 835 000
Commune de Marseille 798 000
SUPERFICIE
SUPERFICIE
EN KM2
FRANCE métropolitaine 549 000
Région PACA 31 400
Département des Bouches-du-Rhône 5 088
Commune de Marseille 240
B
Après La Nouvelle-Orléans, qui a
vu en 1997 la victoire des
Packers 35-21 aux dépens des
New England Patriotes, c’est la côte
Ouest qui accueille le sommet de la
saison NFL (National Football League).
Une saison où personne n’a démontré
de flagrante supériorité.
Difficile donc de parier sur les parti-
cipants à cette nuit magique qui tiendra
en haleine environ 125 000 000 d’Américains
à partir de 15 h 18, heure locale (tout est
programmé à la minute près…), ainsi
que huit cents millions de téléspectateurs
du monde entier, le Superbowl étant
retransmis dans environ 180 pays.
LE XXXIIESUPERBOWL
SE DÉROULE LE 25 JANVIER AU QUALCOMM STADIUM DE SAN DIEGO.
Nuit de folie où il est question de trouver un successeur aux Green Bay Packers…
C
Dans sa tendre enfance, l’Univers
était une boule de pure énergie.
Quelques microsecondes après
sa naissance, sa température
avoisinait mille milliards de
degrés ! Puis, à mesure qu’il se
dilatait, l’Univers se refroidissait
et la lumière se transformait
en particules de matière.
La « soupe » chaude de particules
s’est ensuite coagulée en nuages
de gaz, puis en amas de jeunes
galaxies avant de donner
les galaxies « froides » actuelles.
A
CHRIS BUTLER, BIG-BANG

POUR RÉALISER
LES EXERCICES
20 s’écrit vingt.
80 s’écrit quatre-vingts.
87 s’écrit quatre-vingt-sept.
Mille est invariable.
8 000 s’écrit huit mille.
Trouve, dans les nombres 17 835 927 et 199 609 800 :
– le chiffre des unités de millions ;
– le nombre de millions ;
– le chiffre des dizaines de milliers ;
– le nombre de dizaines de milliers ;
– le nombre de centaines.
1
Observe et complète.
trois cent soixante-… mille … cent vingt
sept … mille soixante
trente-… millions … cent dix mille
… cents
2
Écris en lettres les nombres suivants.
108 200 000 ; 142 900 ; 78 000 240 ; 588 016
3
Place les nombres des étiquettes ci-dessous sur la demi-droite numérique.
4
Trouve tous les nombres que tu peux écrire en utilisant une seule fois
chacun des trois mots : huit, cent, mille.
Écris-les en lettres puis en chiffres.
5
Recopie les nombres dont le chiffre des centaines de milliers est 5,
et ceux dont le nombre de centaines de milliers est 65.
46 582 500 ; 16 358 492 ; 316 250 ; 6 505 351 ;
418 655 ; 5 623 795 ; 126 512 ; 6 525 704
8
Ajoute 100 000 à chacun des nombres suivants et écris le nombre
que tu trouves.
999 ; 61 412 ; 555 400 ; 1 945 000
9
Relie les écritures des nombres qui vont ensemble.
Utilise la calculatrice pour vérifier les calculs.
10
Le Benelux regroupe
trois pays.
Calcule la superficie totale du Benelux.
Exprime la population de chaque pays en milliers d’habitants.
11
Trouve tous les nombres que tu peux écrire en utilisant une seule fois
chacune des quatre étiquettes.
Combien de dizaines a le plus petit nombre que tu as trouvé ?
Combien de centaines a le plus grand nombre que tu as trouvé ?
6
Devinette.
Je suis un nombre compris entre 300 000 et 400 000.
Je suis écrit à l’aide de deux chiffres dont l’un est le double de l’autre et
qui est répété cinq fois.
7
16
POUR RÉALISER
LES EXERCICES
se lit :
cent quarante-huit millions
deux cent quatre mille neuf cent
dix-sept.
chiffre des milliers : 4
nombre de milliers : 148 204
chiffre des dizaines : 1
nombre de dizaines : 14 820 491
1000 s’écrit mille.
1000 000 s’écrit un million.
1000 000 000 s’écrit un milliard.
100 s’écrit cent.
900 s’écrit neuf cents.
910 s’écrit neuf cent dix.
classe des
millions
classe des
milliers
c d u c d
1 4 8 2 0 4
u
9
c
1
d
7
u
22 372 205
22 649 833
568 321 x 39
14 347 237 + 8 024 968
346 372 x 64
34 729 207 – 12 079 374
6 278 492 + 16 662 636
22 167 808
22 941 128
22 164 519
17 825
..58..
.0....
.28..9. .
988 681 605 116 4830 012
trente cent mille cinq
population superficie (en km2)
Belgique 10 200 000 30 513
Pays-Bas 15 700 000 41 785
Luxembourg 410 000 2 586
classe des
millions
classe des
milliers
c d u c d
1 4 8 2 0 4
u
9
c
1
d
7
u
500 000
2 000 000 4 000 000
1000 000 3000 000 5000 000
Chaque mois, le papa de Roxane note le kilométrage de sa voiture.
En utilisant ces données, rédige un court énoncé mathématique
que tu résoudras ensuite.
Voici deux données :
La Terre mesure environ 12 800 kilomètres de diamètre.
Le compteur kilométrique d’une voiture marque 128 000 kilomètres.
Que peut-on calculer ?
Rédige la (les) question(s) et la (les) réponse(s) correspondante(s).
janvier 074 825
février 076 781
mars 079 206
avril 084 538
2
1
17

TRACÉS
cÀ main levée b
Dessine à main levée
sur une feuille blanche :
un triangle qui a un angle droit ;
un triangle qui a ses trois côtés
égaux ;
un carré dont aucun des côtés
n’est horizontal ;
un carré avec
une de ses diagonales ;
un rectangle dont la longueur
est le triple de la largeur.
Après chaque réalisation,
vérifie tes tracés avec l’outil
adapté.
Recommence si tu as fait
des erreurs.
AU CŒUR DES DOCUMENTS
•Pour les angles, ce n’est pas
la longueur des côtés qui est
importante.
•Un angle droit mesure 90°.
On le trace avec une équerre.
•La moitié d’un angle droit
mesure 45°, et le tiers
mesure 30°.
•Un angle plus petit que 90°
est un angle aigu.
•Un angle plus grand que 90°
est un angle obtus.
121
DOCUMENT
❶Cherche le gabarit construit précé-
demment qui recouvre exactement
les angles du panneau. Que cons-
tates-tu ?
DOCUMENT
❶Reproduis schématiquement cette
pyramide.
DOCUMENT
❶En utilisant un des gabarits cons-
truits précédemment, range les
angles dans deux ensembles :
– les angles plus grands que l’angle
droit ;
– les angles plus petits que l’angle
droit.
DOCUMENT
❶Quel(s) gabarit(s) recouvre(nt) l’an-
gle formé par les aiguilles lorsqu’il
est 3h ; 14h30 min ; 18h ; 5h ?
❷Dessine une pendule dont les aiguilles
forment un angle de même mesure
que le gabarit bleu; le gabarit orange;
le gabarit vert. Quelle heure as-tu
représentée sur chaque pendule ?
D
C
B
A
C
Trop, c’est trop !
Les angles
POUR RÉPONDRE
AUX QUESTIONS
Deux angles sont équivalents
lorsqu’on peut les superposer.
Exemple :
AU CŒUR DE LA NOUVELLE POUR ALLER PLUS LOIN
•Reconnaître des angles
superposables.
•Comparer deux angles.
•Construire par pliage
quelques angles
à partir d’un angle droit.
•Ranger des angles.
120
❶Reproduis les différents gabarits pro-
posés. Prolonge leurs côtés. Colorie.
À l’aide de ces gabarits, habille
chaque coin du triangle. Note pour
chacun d’eux la couleur du gabarit
qui convient.
❷Compare :
– deux gabarits de couleur bleue au
gabarit de couleur jaune.
– un gabarit orange ajouté à un
gabarit vert au gabarit jaune.
❶Pour deux triangles, les gabarits que
tu as fabriqués ne suffisent pas.
Trouve une solution en associant plu-
sieurs gabarits. Note les couleurs des
gabarits qui conviennent.
❷Cherche dans l’ensemble de la leçon
le nom que l’on peut donner au
gabarit jaune.
Pourquoi cette tête, les
enfants ?
– C’est la faute de madame
Tressévair, notre maîtresse.
– Ah bon !
– Oui, on a trop de gabarits à faire!
On ne pourra pas venir avec toi en
historoscope.
– Trop de gabarits!
– Oui, Tonton, regarde, il faut fabri-
quer des gabarits pour habiller tous
les coins rouges de ces triangles.
Et pas deux triangles identiques.
On en a pour des heures !
– Mais non, les enfants ! Une feuille
blanche et quatre gabarits vous
suffiront ! dit Eustache. Allez,
départ de l’historoscope dans
cinq minutes. Je vous attends dans
le hangar.
– Il se moque de nous ou il dit
vrai ? » ■
B
A
D
«
abc
df
e

Trace un cercle de centre O et de rayon 5 cm.
Trace un diamètre AB qui ne soit pas horizontal.
Trace une droite passant par O et perpendiculaire à AB.
Sur cette droite, place un point C à 0,7 dm de O.
Joins le point C à A et à B.
Mesure AC et BC. Que constates-tu?
1
123
POUR RÉALISER
LES EXERCICES
angle droit
angle aigu
angle obtus
Décalque les deux angles ci-dessous et découpe-les de façon à obtenir
deux gabarits.
À l’aide des gabarits, recherche les angles qui sont égaux à l’un des deux.
1
Fabriquer des éventails.
On va plier à partir d’une feuille de papier.
Prends un bord de la feuille entre le pouce et l’index et découpe
grossièrement les autres bords pour que seul reste droit celui que tu as saisi .
Plie la feuille en deux comme indiqué en . Tu obtiens ainsi le même gabarit
que celui fait avec le coin de la feuille blanche, mais celui-ci a un pli .
Avec trois feuilles de couleur ayant la même forme au départ, fais
les pliages ci-dessous et sépare chaque gabarit selon le trait fort indiqué.
Tu obtiens ainsi 7 gabarits (un blanc – deux bleus – deux orange –
deux verts). Range les 7 gabarits différents du plus petit au plus grand de
façon qu’on les voie tous un peu quand on fait coïncider un de leurs bords,
et colle ton éventail sur ton cahier.
3
122
POUR RÉALISER
LES EXERCICES
Deux angles sont égaux lorsqu’ils
se superposent exactement.
Exemple :
La valeur d’un angle est indépen-
dante de la longueur de ses côtés.
Exemple :
Reproduis et découpe les gabarits suivants.
Vérifie avec ces gabarits les angles que tu peux mesurer dans les figures
suivantes et complète le tableau.
2
figures
a
b
c
angles utilisés
A
B
C
A
^
D
^
E
^
B
^
C
^
Range ces angles du plus obtus au plus aigu.
4
A
^
C
^
B
^
D
^
E
^
F
^
1 2
1
23
1
1
2
2
3
3
b
a
c

CALCUL MENTAL
cCalcul réfléchi b
Pour multiplier un nombre par
25, il suffit de diviser ce nombre
par 4 et de multiplier le résultat
par 100.
Exemple : 24 x 25
24 l-4 = 6
6x 100 = 600
Calcule :
12 x 25 444 x 25
48 x 25 600 x 25
50 x 25 888 x 25
164 x 25 1 000 x 25
Pour diviser un nombre par 25,
il suffit de multiplier ce nombre
par 4 et de diviser le résultat
par 100.
Exemple : 300 l-25
300 x 4 = 1200
1200 l-100 ➙q = 12
Calcule :
100 l-25
250 l-25
500 l-25
1200 l-25
2000 l-25
AU CŒUR DES DOCUMENTS
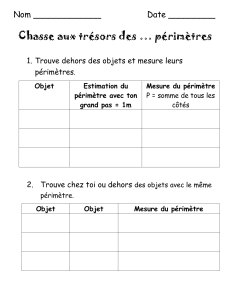
•Pour calculer un périmètre,
on mesure la longueur du
contour d’une figure fermée.
•Si L = longueur et l = largeur
Périmètre du rectangle
= (L + l) x 2.
Si c = côté
Périmètre du carré = c x 4.
147
DOCUMENT
❶Calcule le périmètre de l’espace
de la tente où l’on peut dormir
(personnes allongées) :
– pour la tente à 2 places ;
– pour la tente à 3 places.
DOCUMENT
❶Laquelle de ces trois définitions est
la définition géométrique du mot
périmètre ?
❷Dans quelles circonstances utilise-t-on
les deux autres sens de ce mot ?
DOCUMENT
❶Calcule le périmètre de ce terrain
de football.
❷Calcule le périmètre de la surface
de but.
❸Calcule le périmètre de la surface
de réparation.
C
B
A
Pas mal !
Calculer un périmètre
POUR RÉPONDRE
AUX QUESTIONS
Pour calculer le périmètre d’un
polygone, on ajoute les mesures
de tous ses côtés.
Exemples :
Périmètre du rectangle ABCD :
4 + 2 + 4 + 2 = 12
soit 12 cm
ou
(4 + 2) x2 = 12
soit 12 cm
Le périmètre du rectangle ABCD
est de 12 cm.
4 + 5 + 3 = 12
soit 12 cm
Le périmètre du triangle ABC
est de 12 cm.
AU CŒUR DE LA NOUVELLE POUR ALLER PLUS LOIN
•Calculer le périmètre d’un
polygone quelconque.
•Connaître les formules pour
calculer plus rapidement
le périmètre de certains
polygones réguliers.
146
❶Mesure, sur le plan proposé, les
dimensions et le périmètre de la salle
de bibliothèque avant et après les
travaux.
❷Calcule dans quelle salle on peut
exposer le plus de livres.
❶Avant d’effectuer les travaux, l’archi-
tecte avait proposé d’agrandir la
salle de 2 m sur la longueur et de 2 m
sur la largeur.
Dessine le plan de cette nouvelle salle
en respectant l’échelle.
Calcule quel aurait été alors son péri-
mètre.
Les travaux de la nouvelle salle de la bibliothèque sont
terminés! dit Roxane qui vient d’en
faire la visite avec sa classe.
– Et comment la trouves-tu ?
demande l’oncle Eustache.
–Ce n’est pas mal… Mais il y a moins
de place pour circuler.
–Oui, mais comme il y a des murs
supplémentaires, il y a plus de place
pour ranger les livres… affirme
Julien.
–La salle a donc changé de péri-
mètre? questionne malicieusement
l’oncle Eustache.
–Oui, sans doute! réplique Roxane.
–Tenez! Regardez les plans :
–Dans quelle salle peut-on mettre
le plus de rayonnages fixés au mur
pour exposer les livres ?
–Cela revient bien à chercher leurs
périmètres! constate Julien.
–Eh bien! À vos crayons… » ■
«
A
4 cm
2 cm 2 cm
4 cm
B
DC
A
B
C3 cm
4 cm
5 cm
12 m
6 m
6 m
4 m
12 m
4 m
4 m 4 m
PLANS D’AMÉNAGEMENT
DE LA BIBLIOTHÈQUE
Avant les travaux :
Après les travaux :
C
A
CAMPING
PASSION
Tente de camping
2 ou 3 places.
Forme dôme
avec auvent.
Périmètre
1/ Appareil permettant de mesu-
rer le champ visuel.
2/ Ligne qui définit le contour
d’une figure plane.
3/ Zone quelconque : périmètre de
sécurité.
B