realisation de microcircuit hyperfrequence pour l`excitation et l`etude

Augmentation de la stabilité thermique d’une paroi dans des
nanostructures magnétiques
F. Cayssol1, J.L Menendez1, D. Ravelosona1, C. Chappert1, J. Ferré2, J.P. Jamet2
1Institut d'Electronique Fondamentale, UMR CNRS 8622, Université Paris Sud, 91405
ORSAY Cedex, France.
2Laboratoire de Physique des Solides, UMR CNRS 8502, Université Paris Sud, 91405 Orsay
Cedex, France.
Récemment, il a été démontré que des éléments magnétiques peuvent effectuer des
opérations logiques analogues a celles de l’électronique semiconductrice. Un des avantages de
la logique magnétique est qu’elle permettrait le développement de concepts innovants telle
que la logique reprogrammable. Une proposition très prometteuse dans ce domaine est basée
sur le contrôle précis de la propagation d’une paroi magnétique dans des nanostructures [1]. Il
apparaît donc particulièrement intéressant d’étudier les processus fondamentaux de
propagation de paroi dans des éléments à géométrie confinée. Dans des films magnétiques
continus, le processus de propagation résulte de la compétition entre une énergie élastique qui
tend a rendre la paroi rectiligne et le désordre structural qui rend la paroi rugueuse par
piégeage local. Pour une faible force appliquée sur l’interface, cette compétition entraîne
l’apparition d’un régime de propagation très particulier, présent dans de nombreux systèmes
physiques, la reptation (creep regime). Dans le cas d’un film mince magnétique, le régime de
reptation de paroi est caractérisé par une loi de vitesse qui s’écrit sous la forme v
∝ exp(-
β Uc(Hc/H)
µ
), où β =1/kT , H est le champ appliqué, Hc est un champ critique du aux défauts
structuraux et Uc est une énergie caractéristique. L’exposant
µ dépend du désordre et de la
dimensionnalité du système. Ce phénomène qui dépend des fluctuations thermiques permet de
sonder la stabilité de l’interface dans la limite ou le champ H tend vers 0. Cette loi a été
vérifiée dans des films magnétiques continus 2D pour lesquels
µ =1/4 [2,3].
Pour la première fois à notre connaissance, nous présentons ici une étude approfondie
de la reptation d’une paroi magnétique 1D dans une géométrie confinée 2D [4]. Nous
démontrons que la rugosité de bord de la nanostructure permet d’augmenter la stabilité
thermique de la paroi.
Nous utilisons l’effet Hall extraordinaire (EHE) résolu en temps pour mesurer la
vitesse de propagation v(H) d’une paroi magnétique 1D de type Bloch (largeur 1nm) en
fonction du champ H dans des pistes submicroniques de largeur w0 réalisées dans un système
magnétique modèle: des films épitaxiés de Pt/Co(0.5nm<tCo<1nm)/Pt. Ces couches ultra-
minces de Co présentent une forte anisotropie perpendiculaire, et le retournement de
l’aimantation est dominé par la propagation facile de parois de domaines du à une faible
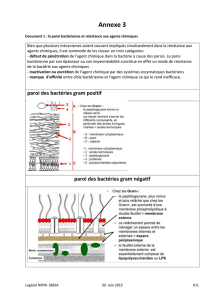
densité de défauts. Sur la figure 1 est tracé logV(H) en fonction de H-1/4 pour des pistes dont
la largeur w0 varie de 0.5 à 1.5 µm. De manière surprenante on observe une forte diminution
de la vitesse de propagation lorsque la largeur de la piste diminue, ce qui indique une forte
augmentation de la barrière d‘énergie pour la propagation. D’autre part, la loi de reptation
v
∝ exp(- β Ucw(Hcw/H)-1/4), valable pour les films continus, est vérifiée pour toutes les largeurs
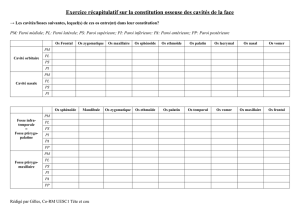
de piste. Finalement, comme l’indique la figure 1(b), le champ critique effectif dans les pistes
Hceff= déduit de la pente des courbes de la figure 1(a), est proportionnel à 1/w
H
Ucw
cw 4
)( β
0
indiquant un effet lié aux bords. Des mesures dans des pistes avec des défauts artificiellement
contrôlés nous montrent que cet effet est du à la présence de la rugosité de bords de la piste
Oral, thématiques 1,3,7

introduite pendant les étapes de nanostructuration. Nous avons développé un modèle
théorique concernant la reptation de paroi dans une piste où les bords présentent une rugosité
corrélée en se basant sur une théorie de piégeage collectif adaptée aux supraconducteurs.
Nous montrons alors en accord avec les résultats expérimentaux que la loi de reptation dans
une piste peut être renormalisée par rapport à un film continu en ajoutant au champ critique
Hc du film continu
Fig. 1(a) : Vitesse moyenne de la paroi en fonction
de H-1/4 pour des pistes de largeurs différentes (1.5,
1, 0.6 et 0.5 microns).
Fig. 1(b) : Champ critique effectif déduit de la
pente des courbes de la Figure 1(a) en fonction
de 1/w0. On observe une nette augmentation de
la barrière d’énergie pour la propagation
lorsque w0 diminue.
0,210 0,215 0,220 0,225 0,230 0,235 0,240 0,245
1E-9
1E-8
1E-7
1E-6
1E-5
1E-4
1E-3
0.5 µm
0.6 µm1 µm1.5 µm
Velocity (ms-1)
H-1/4
0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2
8,0x105
1,0x106
1,2x106
1,4x106
1,6x106
(βUcw)4 HCw (kOe)
1/w0 (µm-1)
(du aux défauts intrinsèques) un champ critique induit topologiquement par la rugosité de
bords et proportionnel à 1/w0 : )/)(/( 0
wka
MHH sccw
σ
+
=
où a est l’amplitude de la
rugosité de bord, k son vecteur d’onde et σ l’énergie de paroi. D’autre part, nous montrons
aussi que cette rugosité de bord permet de diminuer la rugosité de la paroi.
Il apparaît donc que plus le rapport ka/w0 est important, plus la barrière d’énergie que doit
franchir la paroi pour se propager est élevée. Ceci suggère de manière non intuitive qu’une
paroi peut être stabilisée dans un élément de petite dimension par la présence d’une
modulation de bord. Cette augmentation de la stabilité thermique de la paroi est confirmée par
des mesures de vitesse en fonction de la température (10-300K) dans des pistes à forte
rugosité artificielle. Ce résultat est très prometteur pour des applications à la logique
magnétique ou il est nécessaire de pouvoir stabiliser une paroi à une position déterminée dans
un élément de petite dimension..
[1] Allwood et al, Science 296, 5575 (2002).
[2] S. Lemerle et al, Phys. Rev. Lett 80, 849 (1998)
[3] Krusin-Elbaum et al, Nature 410, 444 (2001).
[4] F. Cayssol, D. Ravelosona, C. Chappert, J. ferré, J.P. Jamet, accepté à Physical Review
Letter.