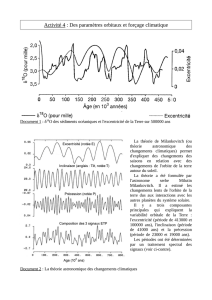
Calculez la masse du Soleil sachant que la Terre tourne autour de

Calculez la masse du Soleil sachant que la Terre tourne autour de celui-ci
avec une période de 365,2563 jours et que le rayon de l’orbite terrestre est
de 149 600 000 km.
commons.wikimedia.org/wiki/File:Sunset_in_Zadar_2.jpg
Découvrez comment résoudre ce problème dans ce chapitre.

Luc Tremblay Collège Mérici, Québec
Version 2016 1 – La gravitation 2
La force de gravitation joue un rôle d’une importance capitale en astrophysique. C’est
pourquoi on commence notre étude de l’astrophysique par l’étude de cette force.
Tous les objets qui ont une masse attirent tous les autres objets qui ont une masse. La force
d’attraction entre deux objets ponctuels est
Loi de la gravitation de Newton (formule générale)
1) Grandeur de la force
12
2
mm
FG
r
où
11 ²
²
6,674 10 Nm
kg
G
2) Direction de la force
Attraction des deux masses l’une vers l’autre
La formule
En astrophysique, on utilise rarement mgy comme formule de l’énergie gravitationnelle
puisque cette formule n’est valide que si on reste près de la surface de la Terre. On doit
donc prendre la formule générale de l’énergie gravitationnelle, qui est
Énergie gravitationnelle (U
g
) (formule générale)
g
GMm
Ur
Dans cette formule, r est la distance entre l’objet et le centre de la planète ou de l’étoile.
L’énergie gravitationnelle est toujours négative et s’approche de zéro à mesure que l’objet
s’éloigne de la planète ou de l’étoile. Ainsi, l’énergie gravitationnelle augmente à mesure
que l’objet s’éloigne de la planète ou de l’étoile.
Notez que quand on calcule l’énergie gravitationnelle d’un objet à proximité d’une planète,
ce qu’on obtient n’est pas l’énergie de l’objet uniquement, mais plutôt l’énergie du système

Luc Tremblay Collège Mérici, Québec
Version 2016 1 – La gravitation 3
planète-objet. Si l’énergie gravitationnelle se transforme en énergie cinétique, l’énergie
cinétique peut donc se retrouver dans l’objet et la planète et non pas uniquement dans
l’objet. La répartition dépend des masses et des contraintes sur le système. Cependant, si
la planète est nettement plus massive que l’objet, l’énergie gravitationnelle ira presque
exclusivement en énergie cinétique de l’objet.
Exemple 1.2.1
Une pierre de 10 kg est immobile à 10 000 km de la surface de la Terre. À quelle vitesse la
pierre va-t-elle frapper la surface Terre (si on fait comme s’il n’y avait pas d’atmosphère) ?
Le rayon de la Terre est de 6378 km et sa masse est 5 974 x 1024 kg.
L’énergie mécanique initiale est
2
11 24
²
²
6
8
1
2
6,674 10 5,974 10 10
016,378 10
2,434 10
terre
Nm
s
GM m
Emv r
kg kg
m
J
Quand l’objet arrive à la surface, son énergie mécanique est
2
11 24
²
²
2
6
28
1
2
6,674 10 5,974 10 10
110
26,378 10
5 6,251 10
terre
Nm
s
GM m
Emv r
kg kg
kg v m
kg v J
En égalant l’énergie initiale à l’énergie à la surface de la Terre, on obtient
82 8
2,434 10 5 6,251 10
8737 m
s
EE
Jkgv J
v

Luc Tremblay Collège Mérici, Québec
Version 2016 1 – La gravitation 4
Sachant que les objets s’attirent par la force de gravitation, on va déterminer comment un
objet très massif modifie la trajectoire des objets qui passent près de lui avec la force de
gravitation qu’il exerce.
Considérons initialement un objet à une certaine distance d’un astre dans la situation
suivante.
Notez que dans cette position initiale, la vitesse et la distance sont perpendiculaires l’une à
l’autre. À cette position, il y a un indice p pour la distance et la vitesse puisque nous
découvrirons dans ce chapitre que ce sont les position et vitesse de l’objet quand est au plus
près de la masse centrale.
On veut savoir la forme de la trajectoire à partir de ce point, ce qui signifie qu’on veut
savoir r en fonction de
. Les détails du calcul de la forme de la trajectoire dépassent le
cadre de cet ouvrage et on va se contenter d’en donner le résultat. La forme de la trajectoire
est
Forme de la trajectoire pour un objet près d’une masse centrale
1
1cos
p
e
rr e
où e est un facteur appelé excentricité qui vaut

Luc Tremblay Collège Mérici, Québec
Version 2016 1 – La gravitation 5
Excentricité
2
1
pp
c
vr
eGM
La forme exacte de la trajectoire dépend de la valeur de e. Nous examinerons les différentes
possibilités dans les sections suivantes.
Nous allons aussi trouver l’énergie mécanique de l’objet qui suit la trajectoire. Cette
énergie est
2
1
2
c
mec p p
GM m
Emvr
Selon la formule de l’excentricité, on a
2
2
1
1
pp
c
c
pp
vr
eGM
GM e
vr
L’énergie devient alors
2
1
2
1
1
2
11
2
12
2
1
2
c
mec p p
cc
pp
c
p
c
p
c
p
GM m
Emvr
GM e GM m
mrr
eGMm
r
eGMm
r
eGMm
r
Ce qui nous donne
Énergie mécanique
1
2
c
mec p
GM m e
Er