image,couleur et interaction

DEVOIR SURVEILLE N°2
PHYSIQUE-CHIMIE
Première Scientifique
DURÉE DE L’ÉPREUVE : 2h00
L’usage d'une calculatrice EST autorisé
CH01 vision et image
CH03 sources de lumière colorée
CH04 interaction lumière-matière
Exercice 1 Image relation de conjugaison (4 points)
On considère une lentille convergente de distance focale f’=5,00 cm. Son centre optique est noté O.
1) Calculez sa vergence C. Donnez le nom de son unité en toutes lettres, et son symbole ?
Représentez à l’échelle 1 la lentille, son axe optique, son centre optique et les foyer F et F’.
2) Un objet lumineux, représenté dans le plan de la figure par une flèche droite AB de 1 cm, est
placé perpendiculairement à l’axe optique, à 15,0 cm devant la lentille. Le point A est situé sur
l’axe optique.
a. Sans calcul, déterminez OA .
b. Déterminez par le calcul 'OA où A’ est le point image de A par la lentille.
c. Calculer la taille
B'
A'
de l’image de
AB
par la lentille, puis calculer le grandissement de
la lentille.
Exercice 2 Loi de Wien (5points)
Donnée : constante de la loi de Wien : 2,898.10
-3
m.K

Exercice 3 Niveaux d’énergie d’un atome (7points)
Le spectre de lumière émise par une lampe à vapeur de sodium fait apparaître principalement
deux raies jaunes, très voisines de longueurs d’onde : λ 2 = 589,0 nm et λ 1 = 589,6 nm.
Données : h = 6,626.10
-34
J.s ; c = 2,998.10
8
m.s
-1
; 1 eV = 1,602.10
-19
J
1) Expliquez la modification que subit un atome de sodium lorsqu’il émet de la lumière.
2) Un atome initialement dans son état fondamental peut-il contribuer à l’émission de lumière ?
3) Les transitions associées aux deux raies jaunes du spectre d’émission du sodium font
intervenir toutes les deux le niveau fondamental de l’atome dont la valeur d’énergie vaut
E 0 = – 5,139 eV.
a. Exprimez et calculez en J et en eV les énergies de transition ΔE 1 et ΔE 2 correspondant à ces
deux émissions de lumière.
b. Exprimez et calculez les valeurs des énergies des niveaux E 1 et E 2 .
4) Représentez sans souci d’échelle la partie du diagramme des niveaux d’énergie identifiés de
l’atome intervenant dans les transitions précédentes. Représentez ces transitions ainsi que
l’émission du rayonnement.
5) Sans calcul, donnez la valeur de l’énergie de transition correspondant à l’absorption d’un
photon d’énergie 3,373.10
-19
J. Justifiez son signe.
6) Dans un diagramme d’énergie, que représente E ∞ ? Quelle est la valeur d’énergie qui lui est
attribuée ?
Exprimez et calculez l’énergie de transition correspondant à la formation de l’ion sodium à partir
de l’état fondamental.
7) N’importe quel photon peut-il être absorbé par l’atome ?Justifier.

Exercice 4 : Interaction lumière-matière (4 points)
1. L’effet photoélectrique
Dans la deuxième moitié du XIX
ème
siècle, comme beaucoup de ses collègues, l’ingénieur allemand
Heinrich Rudolf Hertz consacre l’essentiel de ses recherches au domaine porteur de l’électromagnétisme.
En 1886, il fait une observation troublante.
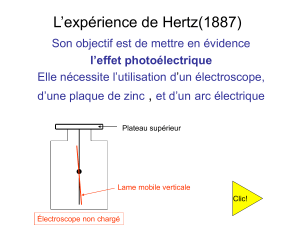
Remarque : un électroscope est constitué d’un plateau relié par un conducteur à deux feuilles conductrices
de masse très faible (feuilles d'or ou de PET métallisé). Une boite métallique avec des fenêtres vitrées
(pour l'observation des feuilles) sert d'écran électrostatique et protège les feuilles des courants d'air.
Quand les feuilles sont chargées, elles portent des charges de même signe qui se repoussent et les feuilles
s'écartent
1
. La déviation est d'autant plus importante que la charge est grande.
Questions
1.1.Pourquoi les feuilles de l’électroscope s’écartent-elles tout d’abord (Fig. 1) ?
1.2.Comment interpréter le fait qu’elles se rapprochent (Fig. 2) ?
1.3.Que se passe-t-il, d’après vous, si l’électroscope était initialement chargé positivement (baguette
d’ébonite frottée sur sac plastique) ?
Hertz interpose également une plaque de verre entre la source lumineuse et le zinc : l’électroscope ne se
décharge alors plus en utilisant la lumière du magnésium ou de la lampe à vapeur de mercure.
1.4.Comment peut-on interpréter l’action de la lame de verre ? Quelles sont visiblement les radiations
qui provoquent l’effet photoélectrique constaté par Hertz ?
Fig. 1
:
Electroscope initialement chargé
négativement : on utilise une baguette de
PVC frottée sur de la laine. Une fois
chargé, les feuilles de l’électroscope
s’écartent l’une de l’autre.
Fig. 2
:
Si la lame est éclairée
« correctement », les feuilles de
l’électroscope se rapprochent.
source de
lumière

CORRECTION DEVOIR SURVEILLE N°2
PHYSIQUE-CHIMIE
Première Scientifique
Exercice 1 image 4 points
On considère une lentille convergente de distance focale f’=5,00 cm. Son centre optique est noté O.
1. La vergence d’une lentille est définie par C = '
1
f et s’exprime en dioptries (
δ
).
Ici : C = =
05,0120
δ
2. On a :
cmABcmOA 0,10,15 =−=
Les conventions employées sont données par le petit signe :
3. La relation de conjugaison s’écrit : '
11
'
1f
OAOA =−
Donc :
==
−
+=+= ''
150,01 050,0 11 '
1
'
1OAoùd
OA
f
OA
4. Le grandissement s’exprime par :
OA
OA
AB
BA ''' ==
γ
On en déduit que : cm
OA
ABOA
BA 6.1
0.9 0.21.7'
'' −=
−×
=
×
=
Exercice 2 5 points
+
+

Exercice 3 niveaux d’énergie d’un atome (7points)
-
1) Un atome émet de la lumière lorsqu’il passe d’un niveau d’énergie supérieure à un niveau
d’énergie inférieure. Il émet alors un photon.
2) Un atome dans son état fondamental possède le niveau d’énergie minimale : il ne peut donc
pas céder d’énergie sous une forme ou une autre. Pour le faire, il doit donc être dans un état
excité correspondant à énergie supérieure à celle de l’état fondamental.
3) a. Lors d’une émission, l’énergie de transition est une grandeur négative qui va être égale à
l’opposée de l’énergie du photon.
Énergie du photon : E = h ν = h c / λ
ΔE 1 = - E 1 = - h c / λ 1 = - 6,626.10 -34 x 2,998.10 8 / 589,6.10 -9 = - 3,369.10-19 J
ΔE 1 = - 3,369.10 -19 / 1,602.10 -19 = - 2,103 eV
ΔE 2 = - E 2 = - h c / λ 2 = - 6,626.10 -34 x 2,998.10 8 / 589,0.10 -9 = - 3,373.10-19 J
ΔE 2 = - 3,373.10 -19 / 1,602.10 -19 = - 2,105 eV
b. Ces transitions se font de l’état excité vers l’état fondamental : E f = E 0 et E i = E 1 ou E 2
Énergie de transition : ΔE a = E f – E i
ΔE 1 = E 0 – E 1 E 1 = E 0 – ΔE 1 = – 5,139 - ( - 2,103) = - 3,036 eV
ΔE 2 = E 0 – E 2 E 2 = E 0 – ΔE 2 = – 5,139 - ( - 2,105) = - 3,034 eV
4) Diagramme d’énergie
E (eV)
E 2 = - 3,034
E 1 = - 3,036
E 0 = - 5,139
5) Cette transition se fait de l’état fondamental vers le niveau d’énergie E 1 : E f = E 1 et E i = E 0
L’énergie de transition correspondante a pour expression : ΔE = E 1 – E 0 avec E 1 > E 0 donc une
grandeur positive avec E(photon) = ΔE = 3,373.10 -19 J
6) E ∞ correspond au niveau d’énergie pour lequel l’électron très excité quitte l’atome. Il lui est
attribué la valeur de 0 eV.
Si l’électron quitte l’atome de sodium, il se forme l’ion sodium et l’énergie de transition
correspondante est :
E f = E ∞ et E i = E 0
Énergie de transition : ΔE ∞ = E ∞ – E 0 = 0,000 - ( - 5,139) = + 5,139 eV
7) Un photon ne peut être absorbé que si l’énergie qu’il transporte correspond à une transition
dans l’atome. Tout autre photon d’énergie différente ne sera pas absorbé.