Exercice n°3 – LA GRELE

2005 USA EXERCICE I – LA GRÊLE ( 4 points )
La grêle se forme dans les cumulo-nimbus situés entre 1000 m et 10000 m d’altitude où la température est très
basse, jusqu’à – 40 °C. Le grêlon tombe lorsqu’il n’est plus maintenu au sein du nuage. Au sol sa vitesse peut
atteindre 160 km/h.
On étudie un grêlon de masse 13 g qui tombe d’un point O d’altitude 1500 m sans vitesse initiale. Il peut être
assimilé à une sphère de diamètre 3,0 cm.
Le point O sera pris comme origine d’un axe Oz orienté positivement vers le bas.
L’intensité de la pesanteur sera considérée comme constante et de valeur go = 9,80 m.s-2.
Données : volume d’une sphère V =
3
3
4
r × π
; masse volumique de l’air ρ = 1,3 kg.m-3
A – CHUTE LIBRE
On admettra que le grêlon tombe en chute libre
1. En appliquant la deuxième loi de Newton, déterminer les équations horaires donnant la vitesse et la position
du centre d’inertie G du grêlon en fonction de la durée t de la chute.
2. Calculer la valeur de la vitesse lorsqu’il atteint le sol, ce résultat est-il vraisemblable ? Justifier.
B – CHUTE REELLE
En réalité le grêlon est soumis à deux autres forces, la poussée d’Archimède
A
F
et la force de frottement fluide
F
proportionnelle au carré de la vitesse telle que F = K×v².
1. Par une analyse dimensionnelle, déterminer l’unité du coefficient K dans le Système International.
2. Donner l’expression de la valeur de la poussée d’Archimède ; la calculer et la comparer à celle du poids.
Conclure.
3. On néglige la poussée d’Archimède.
a) Établir l’équation différentielle du mouvement.
Montrer qu’elle peut s’écrire sous la forme
2
B.vA
dt
dv
−=
b) On veut résoudre cette équation différentielle par une méthode numérique : la méthode d’Euler.
Le tableau suivant est un extrait d’une feuille de calcul des valeurs de la vitesse (v) et de l’accélération (a) en
fonction du temps (t). Il correspond aux valeurs
A = 9,80 m.s-2 et B = 1,56×10-2 m-1, pas de variation ∆t = 0,5 s.
t (s) v(m.s-1) a (m.s-2)
0,00 0,00 9,80
0,50 4,90 9,43
1,00 9,61 8,36
1,50 13,8 6,83
2,00 17,2 a4
2,50 v53,69
3,00 21,6 2,49
Déterminer a4 et v5 en détaillant les
calculs.
c) Exprimer littéralement la vitesse limite
atteinte par le grêlon en fonction de A et
B puis calculer sa valeur numérique.
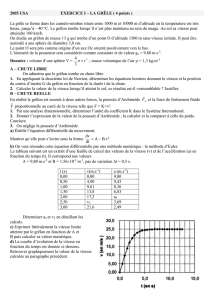
d) La courbe d’évolution de la vitesse en
fonction du temps est donnée ci-dessous.
Retrouver graphiquement la valeur de la vitesse
calculée au paragraphe précédent.

2003 Antilles Exercice II: Réalisation d'une pile nickel-zinc (6,5 points)
On réalise une pile formée à partir des couples Ni2+/Ni et Zn2+/Zn.
Chaque solution a pour volume V = 100 mL et la concentration initiale des ions positifs est
C = 5,0.10-2 mol.L-1.
Données :
M(Zn) = 65,4 g.mol-1
M(Ni) = 58,7 g.mol-1
Charge élémentaire de l'électron: e = 1,6.10-19 C
Constante d'Avogadro: N = 6,02.1023 mol-1 .
Charge d'une mole d'électrons: F = 96500 C
Pour la réaction suivante: Ni2+ + Zn = Zn2+ + Ni, la constante d'équilibre vaut K = 1018.
1. Réalisation de la pile
1.1. L’électrode positive de cette pile est l'électrode de nickel.
Légender le schéma de la figure 1 en annexe (à rendre avec la copie) avec les termes suivants:
électrode de zinc, électrode de nickel, pont salin, solution contenant des ions Zn2+, solution
contenant des ions Ni2+.
1.2. Équation des réactions.
Écrire les demi-équations des réactions se produisant aux électrodes.
Préciser à chaque électrode s'il s'agit d'une oxydation ou d'une réduction.
Écrire l'équation de la réaction globale qui intervient quand la pile débite.
Calculer la valeur du quotient réactionnel initial Qr,i. Cette valeur est-elle cohérente avec la polarité proposée ?
2. Étude de la pile
2.1. On fait débiter la pile dans un conducteur ohmique.
2.1.1. Compléter le schéma de la figure 1.
2.1.2. Préciser sur ce schéma le sens du courant et le sens de déplacement des électrons dans le circuit
extérieur.
2.2. Comment varie la concentration des ions positifs dans chacun des béchers ?
En déduire l'évolution du quotient réactionnel Qr.
2.3. Sachant que la masse des électrodes ne limite pas la réaction, pour quelle raison la pile
s'arrêtera-t-elle de débiter? Quelle est alors la valeur numérique de Qr ?
2.4. La réaction étant considérée comme totale, calculer l'avancement maximal xmax de la réaction.
2.5. Quelle relation existe-t-il entre xmax et la quantité de matière d'électrons qui ont circulé ?
En déduire la quantité totale d'électricité fournie par cette pile.
3. Décharge partielle de la pile
On prend une deuxième pile identique et on la laisse fonctionner pendant une heure. On supposera que
l'intensité reste constante.
On constate une augmentation de masse de l'électrode de nickel de ∆m = 100 mg.
3.1.1. Calculer la quantité de matière d'ions Ni2+ disparus notée ndisp(Ni2+) pendant cette durée.
3.1.2. Déterminer la quantité d'électricité correspondante notée Q.
En déduire la valeur de l'intensité du courant.
3.2. On donne les valeurs de l'absorbance, pour des solutions de sulfate de nickel de concentrations C
différentes, mesurées à une longueur d'onde égale à 390 nm.
C (mol.L–1 ) 0 0,010 0,020 0,030 0,040 0,050
A 0 0,20 0,41 0,61 0,82 1,02
Tracer la courbe de l'absorbance sur la figure 2 en annexe (à rendre avec la copie) en fonction de
la concentration C.
3.3. On mesure l'absorbance de la solution dans laquelle plonge l'électrode de nickel. La valeur mesurée est
A = 0,67.
En déduire graphiquement la concentration des ions Ni2+ restant en solution.
Quelle est la quantité d'ions Ni2+ disparus ?
Ce résultat est-il conforme avec le calcul du 3.1.1. ?

ANNEXE À RENDRE AVEC LA COPIE
Figure 1
A
C (mol.L–1)
0 0,01 0,02 0,03 0,04 0,05
1,00
0,50
0
Figure 2
TOUTES LES ANNEXES, COMPLETEES OU NON, DOIVENT ETRE REMISES
AVEC LA COPIE
+–