Document
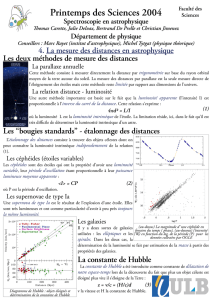
Comment arpenter l’Univers?
L’explosion de la sphère des fixes
Vers 1610, Galilée pointe sa lunette vers la voie lactée et voit des myriades d’étoiles
Panorama à 360° de la Voie Lactée du point de vue terrestre
1. – Méthodes trigonométriques
Plus un objet est proche,
plus il semble grand
Pour l’œil,
« Grand » =
Grand angle
Relation
Angle-distance
Thalès ~ 624-547 ACN
Triangulation
Base de triangulation a
d?
b g
a
Plus d est grand, plus a
doit être grand
d = a/(cotb+cotg)
+ b + g= 180°
sin sin b sin g
a b c
cb
= =
base
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
1
/
37
100%
