TP PHYSIQUE n°12 : Radioactivité, décroissance

T.P. PHYSIQUE n°12 : Radioactivité, décroissance radioactive
1. Stabilité et instabilité des noyaux atomiques :
•
Un atome est constitué par un noyau (très petit, dimension de l’ordre du Femto mètre 1fm=10−15m) situé au
centre d’un espace beaucoup plus grand (de l'ordre de 10–10m) dans lequel se trouvent les électrons.
Le noyau est lui-même constitué de particules appelées nucléons
que l’on peut classer en 2 catégories : les protons et les neutrons.
Compare ces particules :
La représentation symbolique du noyau d'un atome est
A
ZX
X est le symbole de l'élément chimique de numéro atomique Z
Z est le numéro atomique = nombre de protons dans le noyau (appelé aussi nombre de charges)
A est le nombre de masse = nombre de nucléons dans le noyau
N = A–Z est le nombre de neutrons dans le noyau
•
Des noyaux ayant le même numéro atomique Z ont le même symbole X et ils appartiennent au même
élément chimique (par exemple l’élément oxygène si Z=8).
Mais si malgré cela ils n’ont pas le même nombre de nucléons A, ce sont des isotopes.
Donne le symbole de 3 isotopes de l’oxygène :
•
On connaît aujourd’hui plus de 1500 noyaux différents correspondant à seulement 112 éléments chimiques.
Mais seulement 260 d’entre eux sont stables !
Les autres se désintègrent spontanément et évoluent ainsi vers une forme plus stable.
Le diagramme de Segré ci-dessous permet d’étudier comment sont répartis les noyaux stables et instables.
La zone centrale en rouge est appelée « vallée de stabilité ».
A quoi correspond-elle ?
Compare le nombre de protons et le nombre de neutrons
pour les isotopes stables.
Comment trouver les isotopes d'un élément donné ?
Où se situent les noyaux émetteurs β− ?
Quel est leur point commun ?
Où se situent les noyaux émetteurs β+ ?
Quel est leur point commun ?
stables
–
noyaux
Où se situent les noyaux émetteurs α ?
Quel est leur point commun ?
émetteurs β
+
émetteurs β
émetteurs
α
1
Z
1
•
Quelles sont les forces que tu connais qui s’exercent entre les différents nucléons dans un noyau ?
Permettent-elles d’expliquer la cohésion du noyau ?
•
Compare les caractéristiques de la force électrique et de la force nucléaire (particules concernées, portée,
intensité, attractive ou répulsive,...)
•
Explique pourquoi les noyaux "lourds" sont instables et éjectent spontanément une particule α constituée
par 2 protons et 2 neutrons.
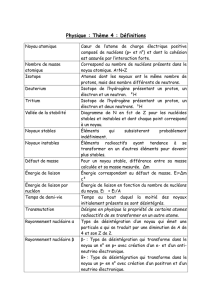
2. Différents types de radioactivité :
Lorsqu’un noyau est instable, il subit une transformation spontanée aboutissant à la formation d’un nouveau
noyau plus stable : ce phénomène porte le nom de radioactivité.
Le noyau « père » donne ainsi naissance à un noyau « fils » : cette transformation radioactive s’accompagne de
l’émission de particules et de rayonnements électromagnétiques.
•
Lois de conservation :
Au cours d’une réaction nucléaire, il y a conservation de la charge électrique (donc du numéro
atomique Z total) et conservation du nombre total de nucléons A.
Caractéristiques des particules émises:
•
4
2
α ou 42He
0 –
β
–1
ou
0 –
e
–1
0 +
β
+1
0 +
ou +1
e
La radioactivité α :
Les particules α sont arrêtées par quelques centimètres d’air ou une feuille de papier.
Le rayonnement α est donc peu pénétrant mais il est très ionisant (altération des membranes cellulaires): il
est dangereux si des poussières radioactives α sont inhalées ou directement en contact avec la peau.
•
La radioactivité β− :
Les particules β− sont assez pénétrantes : il faut plusieurs mm d’aluminium pour les arrêter.
2
•
La radioactivité β+ :
Les particules β+ ont une durée de vie très courte dans la matière car lorsqu’elles rencontrent un électron, les
deux particules s’annihilent en donnant un rayonnement γ .
Remarque: La radioactivité β+ ne concerne que les isotopes créés au laboratoire et qui n'existent pas dans la
nature (radioactivité "artificielle").
Ainsi, une feuille d'aluminium bombardée par des particules α donne des noyaux de phosphore radioactifs β+ :
27
Al
13
capture une particule alpha et réémet immédiatement un neutron.
Un isotope stable de l'aluminium se transmute ainsi en un isotope instable du phosphore
30
15P
qui est radioactif β+
Ecris les équations des réactions nucléaires correspondantes.
•
Le rayonnement γ :
Un rayonnement non chargé, de même nature que la lumière mais de beaucoup
plus grande fréquence, accompagne ces trois types de radioactivité.
Il est émis lorsque le noyau fils, créé dans un état excité noté Y*, évolue vers un état plus stable Y suite à un
réarrangement des nucléons les uns par rapport aux autres.
Il est très pénétrant et nécessite plus de 20cm de plomb pour s’en protéger !
3. Décroissance radioactive :
•
Un noyau instable est susceptible à tout moment de se transformer en un noyau plus stable, grâce à une
transformation nucléaire appelée désintégration.
Mais attention ! un noyau instable ne vieillit pas : il se transforme en un autre noyau d’un seul coup, sans
avoir subi de modifications progressives.
Un noyau jeune a autant de chances de se désintégrer qu’un noyau âgé.
Avant d’avoir subi une désintégration, tous les noyaux sont identiques et il est impossible de prévoir lequel
va se désintégrer en premier : le phénomène de désintégration d’un noyau est aléatoire, c’est à dire qu’il
respecte les lois du hasard, et inéluctable (inévitable) car la probabilité de désintégration d'un noyau est
constante au cours du temps.
•
Ce caractère aléatoire de la désintégration radioactive d’un noyau permet par contre d’interpréter le
comportement d’une population macroscopique (un grand nombre de noyaux identiques) par une loi
statistique et de prévoir ainsi son évolution.
On ne peut pas prévoir l'évolution d'un noyau, mais on peut prévoir l'évolution d'un ensemble
constitué par un grand nombre de noyaux.
•
Analogie avec un lancer de dés (cube en bois dont une face est peinte en rouge)
On lance un dé. Quelle est la probabilité pour que la face supérieure soit rouge ?
Peut-on prévoir, pour un dé donné, au bout de combien de lancer on obtiendra une face supérieure rouge ?
3
Etude théorique:
On dispose d'un échantillon de 1000 dés identiques.
Combien de dés vont présenter la face rouge vers le haut après un premier lancé ?
On élimine les dés qui ont présenté leur face rouge vers le haut, puis on effectue un deuxième lancé avec
les dés restants. Combien de dés vont présenter la face rouge vers le haut après ce deuxième lancé ?
On continue ainsi en suivant les mêmes règles. Complète le tableau ci-dessous, en expliquant comment
tu fais pour remplir une case à partir de la valeur contenue dans la case précédente :
nombre de lancers
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
nombre de dés restants 1000
Que représente un dé qui présente sa face rouge vers le haut dans cette analogie avec l'étude des
désintégrations radioactives?
Et un lancer de dés ?
Trace le graphe représentant le nombre de dés restants en fonction du nombre de lancers.
nombre de dés restants
nombre de lancers
En supposant que l'on effectue un lancer par minute, détermine à partir de cette courbe le temps
nécessaire pour que le nombre de dés restants passe de 1000 à 500, puis de 500 à 250, ou de 800 à 400.
Que constates-tu ?
A quelle date t1 le nombre de dés restants sera-t-il égal à N1 = 400 ?
Peut-on prévoir au bout de combien de temps il ne restera plus de dés ?
4
Vérification expérimentale:
Effectue un premier lancer de 20 dés dans la boite.
Elimine les dés qui présentent leur face rouge vers le haut.
Note le nombre de dés restants dans le tableau ci-dessous, puis relance-les.
Répète l'étape précédente de façon à effectuer 15 lancers.
Ceci constitue une première série de lancers, notée série 1.
Répète le même protocole pour chacune des quatre autres séries.
Additionne pour chaque colonne les valeurs obtenues sur l'ensemble des 5 séries. Remplis la ligne "total"
Peut-on dire que les résultats obtenus sont les mêmes que si on avait effectué une seule série de lancers
avec 100 dés ?
Est-il préférable de lancer 20 dés, 100 dés ou 3000 dés pour essayer de vérifier les résultats théoriques ?
Complète donc la dernière ligne du tableau en prenant en compte les résultats obtenus par l'ensemble
des élèves de la classe.
t
0
Série 1
Série 2
20
20
Série 3
20
Série 4
20
Série 5
20
Total
100
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Classe
Le tableur Excel permet de tracer la courbe expérimentale pour l'ensemble de la classe, ou pour un seul
élève, et de la comparer à la courbe théorique établie précédemment (ramenée à un même nombre initial
de dés).
On note t le numéro du lancer (modélisation du temps qui passe), N le nombre de dés restants.
Que constates-tu ?
4. Activité d'un échantillon radioactif :
L’Activité A d’un échantillon contenant N noyaux radioactifs à une date t
correspond au nombre de noyaux qui se désintègrent par seconde.
Son unité est le Becquerel (Bq) qui correspond à une désintégration par seconde.
Elle peut se mesurer avec un compteur Geiger (voir animation)
La demi-vie t½ d'un isotope donné est la durée nécessaire pour que la moitié de la
quantité initiale de noyaux radioactifs contenus dans l’échantillon se désintègre.
•
Quel type de relation peut-on prévoir entre l'activité d'un échantillon radioactif et le nombre N de noyaux
radioactifs qu'il contient.
•
Comment varie l'activité d'un échantillon radioactif au cours du temps ?
Connais-tu des applications de ce phénomène ?
5