Système International d`Unités

S. Tisserant – PHY11 : Electromagnétisme I - 1
Système International d’Unités
En physique-chimie les grandeurs sont très souvent de natures différentes. Nous ne pouvons,
par exemple, pas additionner une longueur à un volume. Nous caractérisons la nature de
chaque grandeur physique par sa dimension. D’autre part, pour pouvoir exprimer la mesure
d’une grandeur physique nous avons besoin d’associer une unité à toute valeur numérique.
Ces unités font l’objet d’une normalisation internationale. Celle-ci définit unités
fondamentales, unités dérivées, symboles, règles d’écriture ainsi que multiples et sous-
multiples.
A. Unités fondamentales
Les unités fondamentales sont au nombre de sept. Elles sont présentées dans la table suivante
avec leur symbole et la dimension associée.
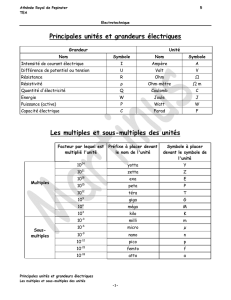
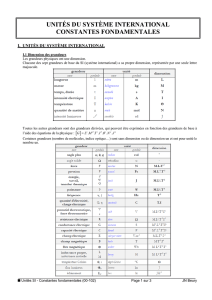
Grandeur Unité Symbole Dimension
Longueur mètre m L
Masse kilogramme kg M
Temps seconde s T
Intensité électrique ampère A I
Température kelvin K Θ
Intensité lumineuse candela cd J
Quantité de matière mole mol N
Table 1 : Les grandeurs fondamentales.
A ces unités fondamentales on ajoute deux unités sans dimension :
Grandeur Unité Symbole
Angle radian rad
Angle solide stéradian sr
Table 2 : Unités fondamentales sans dimension.
B. Equation aux dimensions et unités dérivées
Même si les autres grandeurs physiques peuvent avoir leurs propres unités, elles s’expriment
en fonction de ces unités fondamentales.
La notion de dimension est essentielle pour contrôler la validité d’une relation. Si la
dimension des grandeurs fondamentales s’identifie avec les lettres majuscules indiquées dans
la dernière colonne de la table 1, la dimension d’une autre grandeur X est notée [X]. Celle-ci
peut s’exprimer en fonction des dimensions fondamentales, par exemple :

S. Tisserant – PHY11 : Electromagnétisme I - 2
- une vitesse est homogène à une longueur divisée par un temps : [v] = L⋅T
-1
;
- une surface est homogène au carré d’une longueur : [S] = L
2
.
L’expression de la dimension d’une grandeur en fonction des dimensions fondamentales est
appelée équation aux dimensions.
Il est évidemment impossible de rassembler toutes les grandeurs physiques avec leurs unités
et leurs dimensions. Dans la table suivante nous présentons, à titre d’illustration, quelques
grandeurs physiques, a priori déjà connues.
Grandeur Unité Symbole
Dimension
Surface mètre carré m
2
L
2
Volume mètre cube m
3
L
3
Vitesse mètre(s) par seconde m⋅s
-1
L⋅T
-1
Vitesse angulaire radian(s) par seconde rad⋅s
-1
T
-
1
Accélération mètre(s) par seconde carrée
m⋅s
-2
L⋅T
-2
Fréquence hertz Hz T
-
1
Masse volumique kilogramme par mètre cube
kg⋅m
-3
M⋅L
-3
Force newton N L⋅M⋅T
-2
Pression pascal Pa L
-1
⋅M⋅T
-2
Energie, travail joule J L
2
⋅M⋅T
-2
Puissance watt W L
2
⋅M⋅T
-3
Résistance électrique ohm Ω A
-2
⋅L
2
⋅M⋅T
-3
Conductance électrique siemens S A
2
⋅L
-2
⋅M
-1
⋅T
3
Température Celsius degré Celcius °C Θ
Table 3 : Exemples de grandeurs avec leurs unités et leurs dimensions.
Une équation dont les deux membres sont de même dimension, ce qui doit toujours être le
cas, est dite homogène.
Les fonctions mathématiques (cosinus, sinus, logarithme, exponentielle, etc.) admettent des
arguments sans dimension.
Précisons également quelques règles d’écriture des symboles et des noms d’unités :
- les symboles s’écrivent en minuscules (m, s, sr, etc.) sauf qu’ils correspondent à
l’abréviation du nom propre (Hz, A, N, K, etc.) ;
- les symboles sont invariables, en particulier ils ne prennent pas de s au pluriel (risque de
confusion avec seconde) ;
- les noms d’unités s’écrivent en minuscules, sauf en début de phrase, même s’ils
correspondent à des noms propres et s’accordent ;
- une division de symbole est indiquée par un barre oblique (/) ou par un exposant
négatif ;
- pour éviter les ambiguïtés on ne peut utiliser qu’une barre oblique, à moins d’utiliser
des parenthèses ;
- on ne peut pas combiner symboles et noms d’unités.

S. Tisserant – PHY11 : Electromagnétisme I - 3
C. Multiples et sous-multiples
Les multiples et sous-multiples sont formés à partir de vingt préfixes que nous avons
rassemblés dans la table suivante accompagnés de leurs symboles.
Valeur
Préfixe Symbole Valeur Préfixe Symbole
10 déca da 10
-
1
déci d
10
2
hecto h 10
-
2
centi c
10
3
kilo k 10
-
3
milli m
10
6
méga M 10
-
6
micro µ
10
9
giga G 10
-
9
nano n
10
12
téra T 10
-
12
pico p
10
15
péta P 10
-
15
femto f
10
18
exa E 10
-
18
atto a
10
21
zeta Z 10
-
21
zepto z
10
24
yotta Y 10
-
24
yocto y
Table 4 : Multiples et sous-multiples.
Les préfixes doivent être accolés aux noms d’unités (pas d’espace ni de trait d’union). De
même les symboles des préfixes doivent être accolés aux symboles des unités.