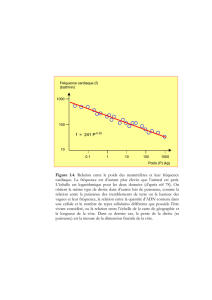
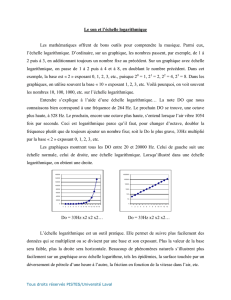
Notes de cours sur les régression non linéaires

Régression pour les modèles autres que linéaires
Lorsqu’on recueille des données expérimentales mettant en relation deux
variables il est souvent intéressant de trouver le modèle mathématique sous-
jacent. Le premier outil dont nous disposons est le diagramme de dispersion. En
effet, il est souvent possible de déceler à première vue le type de fonction qui
met en relation les variables. Dans le cas où les points forment une droite nous
avons vu qu’il était facile de trouver l’équation modélisant les données et même
qu’il était possible de quantifier la qualité d’ajustement des points à notre modèle
linéaire grâce au coefficient de détermination.
Dans les cas où le modèle mathématique est autre que linéaire et afin d’utiliser
les outils que nous possédons déjà, (droite de régression et coefficient de
corrélation); il faudra linéariser les données et par le fait même le modèle
mathématique. Les principaux modèles que nous pourrons linéariser sont :
-le modèle logarithmique : 01
ln
y
kkx=+
-le modèle exponentiel : 01
x
ykk=
-le modèle puissance : 1
0k
ykx=
Comment trouver un modèle non linéaire plausible à partir du diagramme
de dispersion
Les diagrammes de dispersion suivants présentent les modèles plausibles selon
la disposition des points.
Comment linéariser une série de données
Il est possible de linéariser un modèle non linéaire en remplaçant les valeurs de
la variable indépendante (X) ou indépendante (Y) ou encore des deux variables
par leur logarithme. Idéalement il est préférable de reconnaître d’abord le modèle
qui semble s’ajuster le mieux au nuage de points puis vérifier ensuite si ce
modèle est le bon.

Comment vérifier si le modèle décelé est le bon :
Si vous croyez qu’il s’agit d’un modèle exponentiel :
Calculer le logarithme de chacune des valeurs de Y puis retracer le
diagramme de dispersion avec ces nouvelles valeurs. Une autre méthode
consiste simplement à tracer le diagramme de dispersion avec les valeurs
initiales non modifiées, mais cette fois sur du papier semi-log où l’échelle
logarithmique sera sur l’axe des Y. Dans un cas comme dans l’autre, si le
nuage de points s’apparente à une droite c’est qu’il s’agit
vraisemblablement d’un modèle exponentielle.
Si vous croyez qu’il s’agit d’un modèle logarithmique :
Calculer le logarithme de chacune des valeurs de X puis retracer le
diagramme de dispersion avec ces nouvelles valeurs. Une autre méthode
consiste simplement à tracer le diagramme de dispersion avec les valeurs
initiales non modifiées, mais cette fois sur du papier semi-log où l’échelle
logarithmique sera sur l’axe des X. Dans un cas comme dans l’autre, si le
nuage de points s’apparente à une droite c’est qu’il s’agit
vraisemblablement d’un modèle logarithmique.
Si vous croyez qu’il s’agit d’un modèle puissance :
Calculer le logarithme de chacune des valeurs de X et des valeurs de Y,
puis retracer le diagramme de dispersion avec ces nouvelles valeurs. Une
autre méthode consiste simplement à tracer le diagramme de dispersion
avec les valeurs initiales non modifiées, mais cette fois sur du papier log-log
où l’échelle logarithmique sera sur les deux axes. Dans un cas comme
dans l’autre, si le nuage de points s’apparente à une droite c’est qu’il s’agit
vraisemblablement d’un modèle puissance.
Équation du modèle et équation du modèle linéarisé
Voici les relations qui existent entre chacun des modèles et leur modèle linéarisé
Pour le modèle exponentiel :
On peut montrer facilement que :
01
01
01
01
01
ln ln
ln ln ln
ln ln ln qui est une équation de la forme:
si ln , ln et ln
x
x
x
ykk
ykk
yk k
ykxk
yabxa kb k y y
=
=
=+
=+
′′
=+ = = =

On notera évidemment que tel que nous l’avions précisé, on peut obtenir un
modèle linéaire à partir d’un modèle exponentiel si les valeurs de Y sont
remplacées par le logarithme de celles-ci.
NB : On utilise aussi parfois pour le modèle exponentiel la forme suivante :
1
0kx
yke=
De même façon, on peut montrer que :
1
1
1
0
0
0
01
01
01
ln ln
ln ln ln
ln ln ln puisque (ln 1) on aura
ln ln qui est une équation de la forme:
si ln , et que ln
kx
kx
kx
yke
yke
yk e
ykkxe e
ykkx
yabxa kbk y y
=
=
=+
=+ =
=+
′′
=+ = = =
Plusieurs modèles de calculatrice utilisent cette forme de l’équation
exponentielle, le lecteur devra être alors vigilent pour écrire correctement le
modèle mathématique.
Pour le modèle logarithmique
On peut montrer facilement que :
01
01
ln qui est une équation de la forme:
on voit bien ici que , et que ln
yk k x
y
abx ak bk x x
=+
′′
=+ = = =
On notera évidemment que tel que nous l’avions précisé, on peut obtenir un
modèle linéaire à partir d’un modèle exponentiel si les valeurs de X sont
remplacées par le logarithme de celles-ci.
Pour le modèle puissance
On peut montrer facilement que :
1
1
1
0
0
0
01
01
ln ln
ln ln ln
ln ln ln qui est une équation de la forme:
si ln , et que ln et que ln
k
k
k
ykx
ykx
yk x
ykkx
yabx a kbk y y x x
=
=
=+
=+
′′ ′ ′
=+ = = = =

On notera évidemment que tel que nous l’avions précisé, on peut obtenir un
modèle linéaire à partir d’un modèle puissance si les valeurs de X et de Y
sont remplacées par le logarithme de celles-ci.
Comment calculer la droite de régression d’une série linéarisée
Une fois que vous aurez linéarisé vos données, le calcul des coefficients (a et b)
de la droite de régression s’effectuera comme avec des données purement
linéaire. Consulter le volume pour plus de précisions sur le calcul des coefficients
de la droite de régression.

Utilisation de la calculatrice
Il est extrêmement pratique d’utiliser votre calculatrice pour le calcul d’un modèle
mathématique. La difficulté réside toutefois dans la recherche du modèle
adéquat. Il existe une méthode non graphique de recherche du modèle
mathématique basé sur le coefficient de corrélation. Il suffit simplement de
calculer un coefficient de corrélation pour chacun des modèles qu’offre votre
calculatrice. Le modèle mathématique le mieux adapté à vos observations sera
celui qui aura produit le coefficient de corrélation le plus près de 1 ou -1. Pour ce
qui est du calcul des coefficients de votre modèle (généralement a et b sur votre
calculatrice) les valeurs obtenues sont DIRECTEMENT celles recherchées.
Aucun calcul n’est nécessaire. Proprement dit le a que votre calculatrice trouvera
correspond directement à K0 et le b correspond à K1.
Exemples : Voici trois séries de données, trouvons le modèle mathématique le
plus approprié pour chacune d’elle.
Série 1 Série 2 Série 3
x y
x y x y
2 8,9
1 2,2 1 2,00
4 10,9
2 4,9 2 11,31
6 12
3 10,8 3 31,18
8 12,8
4 23,8 4 64,00
10 13,4
5 52,7 5 111,80
12 13,9
6 116,5 6 176,36
14 14,3
7 259,28
Traçons le diagramme de dispersion de chacune des séries :
Série 1
0
2
4
6
8
10
12
14
16
0 5 10 15
Y
X
Diagramme de dispersion