Documents de Physique-Chimie – M. MORIN 1 Devoir de Physique

Documents de Physique-Chimie – M. MORIN
1
Devoir de Physique-Chimie DST3
TS
Durée : 3 h 30 min Date : vendredi 8 avril 2016
M. MORIN
Les calculatrices sont autorisées
I. Etude de quelques molécules et réactions en chimie organiques. 6 points.
1. La palytoxine.
La palytoxine est un puissant vasoconstricteur considéré comme l'une des substances toxiques non-peptidiques les
plus puissantes connues.
Elle a été isolée pour la première fois à Hawaï en 1971 à partir de cnidaires de l'ordre des Zoantharia, et sa
structure chimique a été publiée en 1982. Sa synthèse totale a été réalisée en 1994.
Il s’agit de l’une des molécules naturelles jamais reconstituée par l’homme.
Sa formule brute est C129H223N3O54
Elle possède 64 centres symétriques et 8 doubles liaisons.
1.1 Entourer en bleu 4 doubles liaisons en indiquant si elles sont de configuration Z ou E.
1.2. Placer des astérisques sur 8 carbones symétriques.
1.3. Le carbone asymétrique indiqué par une flèche est de configuration R. Représenter sa configuration S.
1.4. Entourer en rouge 4 fonctions alcools en Indiquant leur classe correspondante (Iaire, IIaire ou IIIaire).
1.5. Entourer en vert, une fonction amide.
1.6. Entourer en noir une fonction amine en indiquant sa classe.
1.7. Les chimistes ne peuvent pas réaliser une synthèse empirique de cette molécule étant donné le très grand
nombre d’isomères possibles. (1019 environ). Il faut qu’il suivre une stratégie de synthèse bien précise. Sa
synthèse a demandée 9 ans de recherche.
Justifier par un calcul ce nombre d’isomères.

Documents de Physique-Chimie – M. MORIN
2
2. Mécanismes réactionnels.
2.1. Représenter les flèches courbes modélisant le mécanisme réactionnel mis en jeu dans la réaction suivante.
A quelle grande catégorie de réactions organiques appartient-elle ?
2.2. Représenter les flèches courbes modélisant le mécanisme réactionnel mis en jeu dans la réaction suivante.
A quelle grande catégorie de réactions organiques appartient-elle ?
2.3. Présentation générale de la réactivité des alcools.
Proposer 4 produits obtenus par les différentes réactions présentées sur le schéma ci-dessus.
2.4. Alkylation des amines. Synthèse de Hoffmann.
Après avoir compléter donner les représentations de Lewis des réactifs, décrire le mécanisme de cette réaction en
utilisant des flèches courbes.
Ecrire la formule topologique du produit obtenu.
+ H+

Documents de Physique-Chimie – M. MORIN
3
2.5. Réaction de l’eau sur un alcène.
Le mécanisme décrit ci-dessus permet d’obtenir l’alcool 1 mais selon la stéréochimie des mécanismes il peut
apparaître d’autres alcools tels que l’alcool 2 et l’alcool 3 représentés ci-dessous
- A quelle grande catégorie de réactions de chimie organique, cette réaction appartient-elle ?
- Indiquer quelles sont les relations existantes entre ces trois différents alcools (identiques, énantiomères ou
diastéréoisomères) ?
Alcool 1
Alcool 2
Alcool 3

Documents de Physique-Chimie – M. MORIN
4
II. La physique dans Star Wars. 9 points.
Partie A : La chute du chasseur TIE.
Lorsque Finn et Poe Dameron ont été touchés par les tirs des soldats du premier ordre, ils sont tombés sur la planète
Jakku.
L’état du TIE tombé au sol, montre qu’il a été soumis à des échanges thermiques importants.
Les échanges thermiques ont lieu dans l’atmosphère puis avec le sol lors de l’atterrissage
Données :
Le chasseur TIE arrive dans l’atmosphère avec une vitesse faible égale à v = 10 m.s-1
Il chute dans l’atmosphère de Jakku d’épaisseur 30 km, que l’on considérera homogène.
La masse du TIE et son équipage est égale à m = 10 tonnes.
La capacité thermique du TIE est égale à ct = 500 J.kg-1.K-1 (notion vue en 1ère S).
Conversion Kelvin-degré Celsius :T (K) = T(°C) +273
La température dans l’espace à 30 km d’altitude est égale à Tinitiale = – 173 °C.
Le rayon de la planète Jakku est égal à R = 5 000 km et sa masse est égale à M = 2,8 × 1024 kg
La constante de gravitation universelle est égale à G = 6,67 × 10-11 u.S.I.
La vitesse d’arrivée du chasseur TIE lors du premier contact au sol est égale à 200 km.h-1.
Il glisse sur le sol sur une distance d = 200 m avant de s’arrêter définitivement.
La vitesse finale au sol est nulle.
Partie A.I. : Chute dans l’atmosphère.
1. Après avoir donné l’expression du champ de gravitation gJ en fonction de M, R et G, régnant sur Jakku, vérifier par
un calcul que sa valeur est égale à 7,5 m.s-2
On considérera que la valeur de la pesanteur dans l’ensemble de cet exercice est constante.
2. Déterminer la valeur de la variation d’énergie potentielle Ep du chasseur TIE entre le moment de sa rentrée dans
l’atmosphère et le premier contact au sol.
3. Déterminer la valeur de la variation d’énergie cinétique Ec entre le moment de sa rentrée dans l’atmosphère et le
premier contact au sol.
4. Toute l’énergie potentielle du TIE s’est-elle convertie en énergie cinétique ? Pourquoi ? Evaluer la valeur de
l’énergie thermique Q dispersée lors de la rentrée dans l’atmosphère.
5. Déterminer la température Tfinale (°C) de la coque du TIE quand il prend contact avec le sol à partir de la relation
suivante : Q = m.ct. (Tfinale- Tinitiale)
m : masse du TIE
ct : capacité thermique massique du TIE
Partie A.II : Freinage sur la surface sablonneuse de Jakku.
1. Dessiner de profil le chasseur TIE et représenter sur votre dessin sans soucis de grandeur, les forces s’exerçant sur
le chasseur TIE lors de son contact avec la surface de Jakku.
2. Donner l’expression des différents travaux des forces mis en jeu sur la distance d.
3. Appliquer le théorème de l’énergie cinétique qui s’écrit Ec = ∑𝑊𝑑
afin d’en déduire la valeur de la force de frottement au sol 𝑓
⃗

Documents de Physique-Chimie – M. MORIN
5
Partie B : Le pistolet laser de Han Solo
Lorsque Han Solo tir sur les soldats de l’empire, il subit un recul de son arme. Le pistolet laser bien que très complexe dans sa
conception, est équipé d’un système relativement simple de compensation du recul.
Il dispose d'un système solide-ressort constitué d'un mobile de masse m = 250 g accroché à l'extrémité d'un ressort à spires non
jointives, de masse négligeable et de raideur k = 10 N.m-l.
Le système de tir laser assimilé à son centre d'inertie G peut osciller horizontalement sur une tige parallèlement à l'axe Ox
(figure 1). On étudie son mouvement dans le référentiel de la planète Hoth supposé galiléen. Le point O coïncide avec la position
de G lorsque le ressort est au repos.
1. Dans un premier temps, on néglige les frottements du mobile sur son rail de guidage.
1.a) Faire l'inventaire des forces exercées sur le mobile.
1.b) Reproduire la figure 1 sur la copie et représenter les différents vecteurs forces sans souci d'échelle.
2. Le mobile est écarté de sa position d'équilibre et lâché à l'instant t = 0 s, sans vitesse initiale, de la position
x0 = + 2,0 cm, et xM > 0.
Calculer la période propre T0 = 2
m
k
du mouvement.
II. On suppose maintenant que les frottements ne sont plus négligeables et peuvent être modélisés par une force dont la valeur
est proportionnelle à celle de la vitesse et dont le sens est opposé à celui du mouvement :
.vf
( > 0).
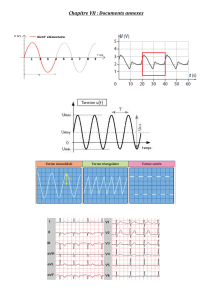
Un dispositif d'acquisition de données permet de connaître à chaque instant la position du mobile (figure 2 sur la page suivante).
Un logiciel de traitement fournit les courbes de variation, en fonction du temps, de l'énergie mécanique (Em) , de l'énergie
cinétique (Ec) et de l'énergie potentielle élastique (Ep) du système solide-ressort (figure 3 sur la page suivante).
1. À l'aide de la figure 2, déterminer la pseudo-période T du mouvement. Comparer sa valeur à celle de la période propre calculée
au I.3.
2. Identifier par leur lettre (A ou B) les courbes de l’énergie cinétique Ec (t) et de l’énergie potentielle Ep(t) de la figure 3 en
justifiant les réponses.
3. Pourquoi l'énergie mécanique du système diminue-t-elle au cours du temps ?
4. Sur les figures 2 et 3 sont repérés deux instants particuliers notés t1 et t2.
En utilisant la figure 2 et en justifiant la réponse, indiquer auquel de ces instants la valeur de la vitesse du mobile est :
a) maximale ; b) nulle.
5. Que peut-on en conclure quant à la valeur de la force de frottement à chacun de ces instants ?
6. Justifier alors la forme « en escalier » de la courbe de l’énergie mécanique Em(t) de la figure 3.
Ainsi, Han Solo peut effectuer une série de tirs, sans prendre le risque d’une luxation de l’épaule !
m
G
O
Figure 1
i
x