Chapitre 5 - Fonction logarithme népérien

TES Chapitre 5 - Fonction logarithme népérien 2012-2013
Chapitre 5 - Fonction logarithme népérien
I La fonction logarithme népérien
TD1 : Fonction exponentielle et réciproque
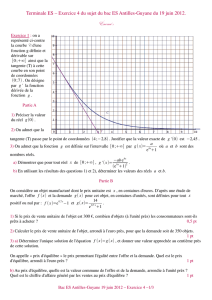
1. Soit fla fonction définie sur Rpar f(x)=ex. On note Cfsa courbe représentative.
(a) Tracer la courbe Cfdans un repère orthonormé d’unité graphique 2 cm, en s’aidant du
graphique donné par la calculatrice (on veillera à laisser l’axe des ordonnées se poursuivre
jusqu’à la valeur −5).
(b) Donner le tableau de variation de fsur R.
(c) Déterminer les solutions des équations f(x)=1et f(x)=e.
(d) Déterminer graphiquement un encadrement d’amplitude 0,5des solutions des équations
f(x)=2et f(x)=3. On note α2et α3ces solutions.
(e) À l’aide de la calculatrice, déterminer une valeur approchée , à 10−2près, de α2et α3.
(f) À l’aide de la calculatrice, conjecturer le nombre de solutions de l’équation f(x)=kpour
kréel, en fonction des valeurs de k.
2. (a) On note ln kl’unique solution de l’équation ex=kpour tout kstrictement positif.
En utilisant la question précédente et sans calculatrice, déterminer ln eet ln 1.
(b) Utiliser la touche ln de la calculatrice pour comparer α2et α3avec ln 2 et ln 3.
3. On note Cgla courbe représentative de la fonction gdéfinie sur ]0; +∞[par g(x)=ln x.
(a) Sur le même graphique que Cf, placer les points de Cgd’abscisses 1,e,α2et α3.
(b) À l’aide de la calculatrice, déterminer les ordonnées des points de Cgd’abscisses 0,1;0,25 ;
0,5et 5.
Tracer alors Cgdans le même repère que Cf.
Rappel : On a vu au chapitre 3 que la fonction exponentielle est une fonction continue et strictement
croissante sur Ret que exest strictement positif.
D’après le théorème des valeurs intermédiaires, quel que soit le réel strictement positif k, l’équation
ex=kadmet une unique solution dans R.
Définition 1
◇On appelle logarithme népérien du réel strictement positif k, l’unique solution de l’équation
ex=k. On note cette solution ln kqui se lit « logarithme népérien de k».
◇La fonction logarithme népérien est la fonction qui, à tout réel strictement positif x, associe
y=ln x.
y=ln xet x>0équivaut à ey=x
-1-

TES Chapitre 5 - Fonction logarithme népérien 2012-2013
On dit que la fonction ln est la fonction réciproque de la fonction exponentielle.
Les courbes représentatives des fonctions ln et exponentielle sont symétriques par rapport à la droite
d’équation y=x(voir TD1).
Propriété
◇La fonction ln est définie et continue sur ]0; +∞[.
◇Pour tout réel x,ln(ex)=xet pour tout réel xstrictement positif, eln x=x.
◇ln 1 =0et ln e=1.
Exemple
ln(e3)=3et eln 3 =3.
Pour tout xréel, ln(e2+ex)=ln(e2+x)=2+x.
Pour tout xréel strictement positif, eln(x+1)+eln(x+3)=(x+1)+x(3)=2x+4.
TD2 : À la découverte d’une dérivée
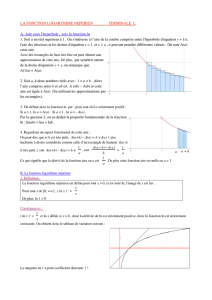
Dans le graphique ci-dessous sont tracés la courbe représentative Cfde la fonction fdéfinie pour
tout xde ]0; +∞[par f(x)=ln x, et les tangentes à Cfaux points A,Bet Cd’abscisses 1,2et 5.
(Rappel : le nombre dérivé de fen x0, noté f′(x0), est le coefficient directeur de la tangente à la
courbe représentative de fau point d’abscisse x0.)
1. À l’aide du graphique ci-dessus, déterminer les valeurs approchées de f′(1),f′(2)et f′(5).
Quelle conjecture peut-on faire sur la valeur de f′(x)pour xréel strictement positif ?
2. Dans cette question, on va utiliser la calculatrice pour vérifier cette conjecture, car elle permet
de calculer une valeur approchée d’un nombre dérivé.
-2-

TES Chapitre 5 - Fonction logarithme népérien 2012-2013
Casio
Sélectionner le menu TABLE.
Dans la ligne Y1, saisir ln(X) .
Dans la ligne Y2, compléter la commande d/dx
en saisissant ln(X),X .
On obtient la commande d/dx avec les touches
OPTN , puis CALC, puis d/dx.
Texas
Appuyer sur la touche f(x)
Dans la ligne Y1, saisir ln(X) .
Dans la ligne Y2, compléter la commande
nbreDérivé( en saisissant ln(X),X,X .
On obtient la commande nbreDérivé( avec les
touches math , puis 8 .
Régler les paramètres de la table pour obtenir des valeurs de xde 0à10 avec un pas de 0,5.
Saisir une formule dans la ligne Y3 qui permette de confirmer la conjecture faite à la question 1.
Propriété
(1) On admet que la fonction ln est dérivable sur ]0; +∞[et ln′(x)=1
x.
(2) La fonction ln est strictement croissante sur ]0; +∞[.
(3) 0<x<1équivaut à ln x<0et x>1équivaut à ln x>0.
(4) Pour tous réels aet bstrictement positifs, a=béquivaut à ln a=ln bet a<béquivaut à
ln a<ln b.
Démonstrations :
(2) La fonction ln est dérivable sur ]0; +∞[et sa dérivée xz→ 1
xest strictement positive sur cet
intervalle donc la fonction ln est strictement croissante sur ]0; +∞[.
(3) En appliquant la fonction ln, strictement croissante, à l’inégalité 0<x<1, on obtient : ln x<ln 1
soit ln x<0. De même si x>1alors ln x>0.
(4) Cette propriété se déduit de la stricte croissance de la fonction ln.
Exemple
0<7
11 <1donc ln 7 11<0et 15 13 >1donc ln 15 13>0.
Sur ]0; +∞[,ln(x+2)=ln 3 si et seulement si x+2=3soit x=1.
II Relation fonctionnelle du logarithme népérien
TD3 : Additionner pour calculer un produit
1. (a) À l’aide de la calculatrice, donner des valeurs approchées à 10−3près de :
A=ln 5 +ln 7 ;B=ln 3 +ln 11 ;C=ln 13 +ln 6 ;D=ln 33 ;E=ln 78 ;F=ln 35.
Quels regroupement peut-on faire ?
(b) Compléter le tableau ci-dessous et émettre une conjecture.
a2 4 3 5 40
b3 7 10 2 27
ln a+ln b
ln(ab)
-3-

TES Chapitre 5 - Fonction logarithme népérien 2012-2013
2. En utilisant la relation fonctionnelle de la fonction exponentielle, comparer
eln a+ln bet eln(ab)pour aet bréels strictement positifs. Que peut-on en
déduire ?
3. Les tables de logarithmes de Néper permettaient, à une époque sans calcu-
latrice, d’effectuer plus rapidement des multiplications grâce à la relation :
ln a+ln b=ln(a×b)pour tous réels positifs non nuls aet b.
En se servant uniquement de l’extrait de table de logarithmes ci-contre et
de la relation précédente, donner une valeur approchée de 15,3×7.
xln x
6,9 1,931
7 1,946
7,1 1,960
... ...
15,1 2,715
15,2 2,721
15,3 2,728
... ...
107,1 4,674
107,2 4,675
107,3 4,676
Théorème
Pour tous réels aet bstrictement positifs, ln(a×b)=ln a+ln b.
On dit que la fonction ln vérifie la relation fonctionnelle suivante : f(a×b)=f(a)+f(b)pour tous
réels aet bstrictement positifs.
Exemple
ln 5 =ln(3×5)=ln 3 +ln 5.
ln 10 −ln 14 =ln(2×5)−ln(2×7)=ln 2 +ln 5 −(ln 2 +ln 7)=ln 5 −ln 7.
Pour x∈]1; +∞[:ln(x−1)+ln(x+1)=ln((x−1)(x+1))=ln(x2−1).
Si dans la relation fonctionnelle, on prend a=b, on obtient : ln(a×a)=ln a+ln asoit ln(a2)=2 ln a.
De la même façon, on obtient :
ln(a3)=ln(a2×a)=2 ln a+ln a=3 ln aet ln(a4)=ln(a3×a)=3 ln a+ln a=4 ln a.
On peut généraliser avec la propriété suivante :
Propriété
Pour tout entier naturel net tout réel astrictement positif : ln(an)=nln a
Exemple
ln(54)=4 ln 5 ;ln 8 −ln 4 =ln(23)−ln(22)=3 ln 2 −2 ln 2 =ln 2.
Propriété
(1) Pour tout réel bstrictement positif, ln 1
b=−ln b.
(2) Pour tous réels aet bstrictement positifs, ln a
b=ln a−ln b.
(3) Pour tout entier naturel net tout réel astrictement positif, ln(a−n)=−nln a.
(4) Pour tout réel astrictement positif, ln √a=1
2ln a.
-4-

TES Chapitre 5 - Fonction logarithme népérien 2012-2013
Démonstrations :
(1) On a 1
b×b=1donc ln 1 b×b=ln 1 donc ln 1 b+ln b=0donc ln 1 b=−ln b.
(2) On a a
b=a×1 bdonc ln a b=ln a×1 b=ln a+ln 1 b=ln a−ln b.
(3) a−npeut s’écrire 1
andonc ln(a−n)=ln 1 an=ln 1 −ln(an)=0−nln a=−nln a.
(4) On a 2 ln √a=ln √a2=ln adonc ln √a=1
2ln a.
Exemple
Pour aet bréels de ]0; +∞[,ln a7
b+2 ln(a−3)=7 ln a−ln b+2×(−3)ln a=ln a−ln b.
1
2ln 25 +2 ln √3=ln √25+2×1 2ln 3 =ln 5 +ln 3.
III Équation xn=ket concavité de la fonction ln
III.1 Équation de la forme xn=k
TD4 : Une nouvelle équation
1. On donne les représentations graphiques des fonctions fndéfinies sur Rpar fn(x)=xnpour
n=2,3,4et 5. Dresser le tableau de variation de chacune de ces fonctions sur R.
2. (a) Soit kun réel positif. À l’aide de l’animation sur Geogebra, donner le nombre de solutions
sur ]0; +∞[de l’équation xn=k, où nest un entier naturel.
(b) Par lecture graphique, donner une valeur approchée de la solution de l’équation x5=20.
3. On admet que, pour tout kpositif, l’équation xn=kadmet une unique solution positive quel
que soit l’entier naturel n.
(a) Vérifier que le réel x=eln k
nest la solution de l’équation xn=k.
(b) En déduire la valeur exacte de la solution de l’équation x5=20 et comparer avec la réponse
donnée à la question 2.(b).
-5-