SUITES NUMÉRIQUES 1ère S DEVOIR SURVEILLÉ - ambition

Première'S'Devoir'surveillé'Mme'MAINGUY'
'
!
!
!
!
!
!SUITES NUMÉRIQUES 1ère S
DEVOIR SURVEILLÉ
!
!
!
!
Exercice 1
1) Dans!chacun!des!cas!ci-dessous,!calculer!les!quatre!premiers!termes!de!la!suite!
un
( )
!:!
cas'1':!pour!tout!
n∈!∗
,!!!
un=−1
( )
n
+6
n
!
! !
u1=−1
( )
1+6
1=−1+6=5 ; u2=−1
( )
2+6
2=1+3=4
u3=−1
( )
3+6
3=−1+2=1 ; u4=−1
( )
4+6
4=1+3 2=5 2
!
!
cas'2':!
u0=2
pour tout n≥1, un=un−1
( )
2−10n+3
⎧
⎨
⎪
⎩
⎪
!
!
!
u0=2 ; u1=u0
( )
2−10 ×1+3=22−10 +3=−3
u2=u1
( )
2−10 ×2+3=−3
( )
2−20 +3=−8 ; u3=u2
( )
2−10 ×3+3=−8
( )
2−30 +3=37
!
!
!
2) On!considère!la!suite!
vn
( )
!définie!pour!tout!entier!naturel,!par!:!
vn=3n−4
.!
Calculs!de!
vn+1,vn+1, vn−1,vn−1
!:!
! ! ! ! !
vn+1=3n+1
( )
−4=3n+3−4=3n−1
vn+1=3n−4+1=3n−3
vn−1=3n−1
( )
−4=3n−3−4=3n−7
vn−1=3n−4−1=3n−5
!
!
!
!
Exercice 2
Soit!la!suite!
un
( )
!définie!par!:!
u0=0,2
!et!pour!tout!
n∈!
,!!!
un+1=1
4
un
2+1
.!
!
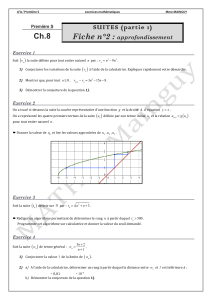
1) Construction!dans!le!repère!orthonormé!ci-dessous!des!cinq!premiers!termes!de!la!suite!(construction!en!
chemin).!
On!placera!les!termes!de!la!suite!sur!l’axe!
Ox
( )
.!
!

Première'S'Devoir'surveillé'Mme'MAINGUY'
'
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
2) Par!lecture!graphique,!il!semble!que!
lim
+∞
un=2
.!!
En!effet,!la!suite!
un
( )
!est!définie!par!une!relation!de!récurrence!de!la!forme!
un+1=f un
( )
!avec!
f
!fonction!définie!
sur!
0 ; +∞
⎡
⎣⎡ ⎣
!par!:!
f x
( )
=1
4x2+1
.!Sur!le!graphique,!on!a!tracé!la!courbe!
Cf
!et!la!droite!d’équation!
y=x
.!La!limite!!
est!l’abscisse!(ou!l’ordonnée)!du!point!d’intersection!de!cette!droite!et!de!
Cf
.!
!
3) On!admet!que!la!suite!
un
( )
!admet!une!limite!finie!
l
!lorsque!
n
!tend!vers!
+∞
.!
La!limite!
l
!vérifie!l’équation!
l=f l
( )
.!On!a!alors!:!!
! ! !
l=1
4
l2+1⇔1
4
l2−l+1=0
⇔l2−4l+4=0
⇔l−2
( )
2
=0
⇔l=2
!
!
4) a/!Algorithme!an!langage!naturel!qui!affiche!le!rang!
N
!à!partir!duquel!
un−l<10−4
.!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
Variables':! !sont!des!nombres.!
!
Début':!! Affecter!à! !la!valeur! !
!Affecter!à! !la!valeur! !
!
Traitement':!! Tant!que! !faire!
!Affecter!à! !la!valeur! !
!Affecter!à! !la!valeur! !
!Fin!Tant!Que!
!
Sortie':!! Afficher! !

Première'S'Devoir'surveillé'Mme'MAINGUY'
'
!
!
b/!!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
5) On!pose!maintenant!
u0=2,2
.!
a/!Algorithme!en!langage!naturel!qui!affiche!en!sortie!la!valeur!de!
un
,!pour!
n
!entré!par!l’utilisateur!:!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
b/!Programmer!cet!algorithme!sur!calculatrice!et!donner!les!valeurs!de!
u10 ,u25 et u30
.!
!
!
!
!
!
!
!
!
!
!
!
!
!
Variables':! !sont!des!nombres.!
!
Début':!! Affecter!à! !la!valeur! !
!
Traitement':!! Pour! !allant!de! !à! !
!Affecter!à! !la!valeur! !
!Fin!Pour!
!
Sortie':!! Afficher! !

Première'S'Devoir'surveillé'Mme'MAINGUY'
'
!
!
Exercice 3
!
Une!chaîne!de!télévision!est!implantée!dans!trois!villes!A,!B!et!C.!Elle!propose!des!abonnements!que!l’on!peut!renouveler!
ou!non!tous!les!trimestres.!
!
Voici!ses!résultats!actuels!:!
-'Ville'A':!1000!abonnés!et!320!abonnés!supplémentaires!tous!les!trimestres.!Les!abonnés!sont!satisfaits!et!se!réabonnent!!
!!!!!tous.!
-'Ville'B':!400!abonnés!et!une!progression!de!10%!tous!les!trimestres.!Les!abonnés!sont!satisfaits!et!se!réabonnent!tous.!
!
-'Ville'C':!1500!abonnés!mais!à!chaque!fois,!seulement!80%!des!abonnés!se!réabonnent.!Ils!sont!en!revanche!rejoints!par!!
!!!!600!abonnés!supplémentaires!chaque!trimestre.!
!
On!nomme!
an
,!
bn
!et!
cn
!le!nombre!d’abonnés!dans!les!villes!A,!B!et!C!après!
n
!trimestres!pour!
n≥0
.!
On!a!donc!
a0=1000
,!
b
0=400
!et!
c0=1500
.!
!
1) En!utilisant!les!données!de!l’énoncé,!déterminer!les!valeurs!de!
a1
,!
b
1
!et!
c1
.!
a1=1000 +320 =1320
!!!;!!!
b
1=400 +10
100
×400 =440
!!!!;!!!
c1=80
100
×1500 +600 =1800
!
!
!
2) On!veut!comparer!l’évolution!des!nombres!d’abonnés!dans!les!villes!A,!B!et!C!au!bout!des!40!premiers!trimestres.!
a/!Voici!les!dernières!lignes!de!la!feuille!de!calcul!:!
!
! ! !
!
!
!
!b/!Formules!entrées!dans!les!cellules!A3,!B3,!C3!et!D3!:!
!!!!!!Formule!dans!la!cellule!A3!:!!!
=
!A2
+1
!
!!!!!!Formule!dans!la!cellule!B3!:!!!
=
!B2
+
320 !
!!!!!!Formule!dans!la!cellule!C3!:!!!
=
!C2
+0,1×
C2 !
!!!!!!Formule!dans!la!cellule!D3!:!!!!
=
!
0,8 ×
D2
+600
!
!
!
!
3) Il!semble!que!dans!la!ville!A,!le!nombre!d’abonnés!continuera!à!progresser!avec!régularité!;!dans!la!ville!B,!le!
nombre!d’abonnés!semble!augmenter!d’un!trimestre!à!l’autre.!Quant!à!la!ville!C,!le!nombre!d’abonnés!semble!
stagner!à!une!valeur!proche!des!300!abonnés.!
!
!

Première'S'Devoir'surveillé'Mme'MAINGUY'
'
!
Exercice 4
Soit!
vn
( )
!la!suite!définie!par!
v1=1
!et,!pour!tout!
n≥1
,!!!!
vn+1=1
1+1
vn
.!
1)
v1=1 ; v2=1
1+1
v1
=1
1+1
1
=1
2;v3=1
1+1
v2
=1
1+1
1
2
=1
1+2
=1
3;v4=1
1+1
v3
=1
1+1
1
3
=1
1+3
=1
4
!!!!!!;!…!
Il!semble!donc!que!pour!tout!
n≥1
,!on!ait!:!
vn=1
n
.!
2) Soit!
wn
( )
!la!suite!définie!pour!tout!
n≥1
,!par!
wn=1
n
.!
On!a!alors!:!
w
1=1
1
=1
.!
De!plus!:!
1
1+1
wn
=1
1+1
1
n
=1
1+1×n
1
=1
1+n
=wn+1
.!
Ainsi,!on!a!
v1=w
1
!et!pour!tout!entier!
n≥1
,!
wn=vn=1
n
.!Les!deux!suites!
vn
( )
!et!
wn
( )
!sont!alors!égales.!
3) Les!suites!
vn
( )
!et!
wn
( )
!étant!égales,!elles!ont!les!mêmes!variations.!
La!suite!
wn
( )
!est!de!la!forme!
wn=f n
( )
!et!la!fonction!
f
!est!la!fonction!inverse.!
La!suite!
wn
( )
!et!la!fonction!
f
!ont!les!mêmes!variations.!
La!fonction!inverse!étant!décroissante!sur!
0 ; +∞
⎤
⎦⎡ ⎣
,!on!en!déduit!que!les!suites!
wn
( )
!et!
vn
( )
!sont!décroissantes.!
!
Exercice 5
Faustin!propose!à!son!amie!Soline!le!marché!suivant!pendant!vingt!jours.!
«!Le!premier!jour!tu!me!donnes!un!euro!et!je!t’en!donne!10!;!le!second,!tu!m’en!donnes!
22
!et!je!t’en!donne!20,!le!troisième!
tu!m’en!donnes!
32
!et!je!t’en!donne!30,!et!ainsi!de!suite.!»!
On!note!
un
!le!nombre!de!bonbons!perdus!ou!gagnés!par!Faustin!le!
n
-ième!jour.!Ainsi,!
u1=1−10 =−9
.!
1) Calcul!de!
u2,u3,u4et u5
!:!
u2=22−20 =−16 ; u3=32−30 =−21 ; u4=42−40 =−24 ; u5=52−50 =−25
!
!
2) On!a!donc!pour!tout!entier!naturel!
n≥1
,!!
un=n2−10n
.!
Variations!de!la!suite!
un
( )
!:!étudions!le!signe!de!
un+1−un
!:!
un+1−un=n+1
( )
2
−10 n+1
( )
−n2−10n
( )
=n2+2n+1−10n−10 −n2+10n
=2n−9
!
2n−9>0⇔n>9
2
!
conclusion!:!pour!
n
!compris!entre!1!et!5,!
un+1−un<0
,!la!suite!
un
( )
!est!strictement!décroissante.!
! ! !!!!!!!!pour!
n≥5
,!
un+1−un>0
,!la!suite!
un
( )
!est!strictement!croissante.!
!
3)
u20 =202−10 ×20 =400 −200 =200
.!
Au!bout!de!vingt!jours,!Faustin!aura!gagné!200!bonbons.!
!