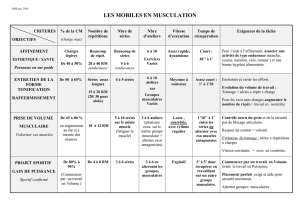
Probabilités : Exercice de piles et faces en prépa BCPST

Exercice de khôlle de maths sur les probabilités, prépa
BCPST: Séries de piles et de faces
Mise en contexte :
Cet exercice, dont l’énoncé est dans l’encadré un peu plus bas, m’a été donné lorsque j’étais
en première année de classe prépa filière BCPST, à l’occasion d’une khôlle de maths. Il se base sur le
jeu de pile ou face, et fait intervenir insidieusement la loi des séries.
Mais tout d’abord, qu’est-ce que la loi des séries ? C’est une loi qui dit grosso modo que si
un événement assez exceptionnel se produit, cela entraîne des événements de même type à se
produire à sa suite, comme si ces événements s’attiraient (typiquement: « un malheur n’arrive
jamais seul »). Peut-être vous souvenez-vous des 3 crashs de trains en Europe (et 1 au Québec) en
Juillet 2013 ? A l’époque les médias avaient en toutes lettres invoqué la loi des séries. Idem pour les
5 crashs d’avions en 22 jours de l’été 2005, sauf que là une explication mathématique (qui avait fait
l’objet de plusieurs articles de journaux) invoquant la loi des probabilités (et non des séries) a été
proposée : environ 20 00 vols ont lieu chaque jour, et il y a en moyenne un crash (enfin, un accident,
qu’il soit relativement mineur ou assez majeur, au décollage comme ailleurs durant le vol) tous les
500 000 vols, ce qui fait 1 chance sur 10 que 5 crashs se produisent en 22 jours !
Bref, on pourrait alors penser que cette loi des séries n’est qu’un artefact médiatique (un
drame incite les médias à relater plus d’histoires impliquant ce même drame, histoire de faire dans
le sensationnel, et le commun des mortels pense alors qu’un drame en appelle un autre identique).
Mais, au risque de gâcher la surprise, l’exercice proposé ici est (à mon sens) une super illustration
que cette loi existe… sous certaines conditions ;) A l’époque ça m’avait décoiffé ! Et 4 ans et demi
plus tard j’arrive enfin à le refaire, avec quelques conseils de ma prof de maths de spé, Florence
Gaja, et poussé par des interrogations de quelques amis à qui j’avais parlé de cette fameuse loi et de
cet exercice.
J’ai essayé d’être le plus rigoureux possible au niveau mathématique tout en essayant de
rendre le contenu accessible à pas mal de niveaux différents en maths (d’où les lignes et les lignes
d’explications, afin de notamment traduire en français le langage mathématique :) ). Notamment, les
principaux résultats sont encadrés et en rouge, histoire que ceux qui ne veulent pas s’embêter avec
les démonstrations puissent trouver facilement les réponses ;) Si vraiment vous n’avez que 5
minutes à accorder à cet exercice, sa réponse se trouve au point 5), et sa transposition dans la
« vraie vie » au point 8) ! J’espère avoir limité au maximum les erreurs et les interprétations ou
explications imprécises voire limite incorrectes. Bref, allumez vos cerveaux, c’est parti !
Kévin Maurin, Mai 2015

L’énoncé :
On lance plusieurs fois une pièce de monnaie ayant une probabilité p de donner pile (P) et 1-p de
donner face (F). Les lancers sont indépendants.
Cette séquence de piles et de faces constitue des séries d’un même côté de pièce, que l’on
numérote. Ce numéro augmente à chaque fois qu’une nouvelle série commence (voir l’exemple ci-
dessous).
Côté de pièce PPP FFFFF PPPP FF PPPP F PPPP FFFFFF P
Suite numéro 1 2 3 4 5 6 7 8 9
Question : calculer la longueur moyenne des séries de numéros pairs.
Résolution :
Commençons d’abord par les définitions des lettres qui vont apparaître par la suite (histoire
de savoir de quoi on parle !) :
- La longueur d’une série d’un même côté de pièce : variable aléatoire notée , qui prend
des valeurs (une série infinie d’un même côté de pièce est improbable, mais pas
impossible (on dit alors quasi-impossible), ce qui est une différence importante en maths
– et qui devrait l’être un peu plus dans la « vraie vie » ;) )
- Le numéro d’une série : . Enfin, pas tout à fait : les séries de numéros pairs seront
notées (2n donnant alors des numéros pairs, qui commencent bien à 2 qui est le
premier numéro pair de série, pour : 2, 4, 6, 8…) et les séries de numéros impairs
notées (2n-1 donnant alors des numéros impairs, qui commencent bien à 1 qui est
le premier numéro impair de série, pour : 1, 3, 5, 7…)
1) L’idée pour calculer la probabilité qu’une série de F soit de longueur k : il faut que l’on
fasse k F de suite après une série de P, et faire un autre P à la fin qui termine la série de F. Chaque F
ayant une probabilité 1-p et le P une probabilité p de sortir, on en déduit que la probabilité qu’une
série de F soit de longueur k est donnée par :
Suivant le même raisonnement, la probabilité qu’une série de P soit de longueur k est
donnée par :
Là, il y a un petit point conceptuel : pourquoi mettre exposant k-1 et non k ? Ma prof m’a
expliqué qu’il ne faut pas compter le premier jet d’une série car il est indispensable pour commencer
la série, sans lui la série n’existe pas. En gros la probabilité que le premier jet d’une série soit de
même nature que la série qu’il commence est de 1, donc il n’y a que k-1 P qui ont une vraie
probabilité p de sortir sur les k P que compte la série (ou du moins c’est comme ça que je l’ai

compris – et le raisonnement est le même pour les F). Ce n’était pas mon raisonnement quand
j’avais fait l’exercice à l’époque (enfin je crois – je ne m’en souviens plus à vrai dire…), mais ça donne
le même résultat final alors bon ^^’
2) Avant de vraiment s’intéresser à l’aspect pair ou impair des numéros des séries,
commençons par chercher la probabilité de la longueur d’une série indépendamment de sa nature
(c’est-à-dire qu’elle soit de P ou de F).
Il faut pour cela utiliser la formule des probabilités totales, ce que l’on peut faire car
l’ensemble des événements {« c’est une série de P » ; « c’est une série de F »} est un système
complet d’événements (il n’y a que 2 types de série possibles avec deux côtés de pièce). En toutes
lettres d’abord, la formule dit alors :
« La probabilité qu’une série soit de longueur k » = « la probabilité qu’une série soit de
longueur k sachant que c’est une série de F » x « la probabilité que ce soit une série de F » + « la
probabilité qu’une série soit de longueur k sachant que c’est une série de P » x « la probabilité que
ce soit une série de P »
Puis en langage plus mathématique :
Or on connaît les deux probabilités conditionnelles (voir point 1) ) :
Equation (1)
Les deux dernières inconnues, à savoir les probabilités que l’on parle d’une série de F ou de
P, vont dépendre de si l’on s’intéresse à des séries de numéros pairs ou impairs.
3) Maintenant, comment formaliser dans le calcul qu’une série est de numéro pair ? Ce qui
était le super problème que j’ai eu en essayant de refaire l’exercice ^^
Si on jette un œil à l’énoncé plus haut, on remarque que les séries de numéros pairs sont des
séries de F. Si l’on veut que les séries de numéros pairs soient des séries de P, on voit qu’il suffit de
remplacer chaque F par un P et vice-versa.
Ce qui change ? Tout bien sûr, mais en particulier le tout premier jet : si les séries de
numéros pairs sont des séries de F, c’est un P, et vice-versa ! C’est donc « tout simplement » le côté
de pièce sorti au premier jet qui détermine de quelle nature sont les séries de numéros pairs !
Donc, pour des séries de numéros pairs :
et

4) Désormais, on peut intégrer l’aspect « numéro pair de la série » pour répondre à la
question de l’énoncé.
On obtient alors enfin la probabilité qu’une série de numéro pair soit de longueur k :
Je laisse volontairement les carrés développés pour faire la différence entre le tout premier
jet, qui donne le caractère pair au numéro de la série, et le jet qui termine la série.
5) Et ENFIN, on peut répondre à la question de l’énoncé, en calculant l’espérance de
(l’espérance mathématique étant le moyen de donner la vraie valeur moyenne d’une
variable aléatoire), avec la formule :
Je vous passe le calcul, mais pour ceux qui veulent s’amuser à le refaire, un petit rappel ;)
Et Ô magie, miracle, THE résultat qui sur le coup m’a fait regarder mon tableau en mode
« WTF ? » en cherchant l’erreur :
Oui, simplement 2. La longueur d’une suite de numéro pair a en moyenne une longueur de
2, et ce même si la pièce est truquée (ce qui est le truc le plus ouf de cette histoire !). Mais je
reviendrai là-dessus un peu plus bas (voir point 8) ).
6) Comme j’avais fini ces calculs en à peine 20 minutes à l’époque (alors qu’au cumulé, j’ai
bossé presque 4h30 à refaire cet exercice maintenant (sans compter le temps passé à rédiger ce
document) – comme quoi quand on quitte la prépa y’a des réflexes qui se perdent !), et qu’une
khôlle dure normalement 1h, le prof m’avait fait calculer d’autres choses sur le même exercice.
Heureusement pas de variances, que je n’ai d’ailleurs pas envie de calculer maintenant non plus (ça
n’illustre pas mieux le propos de toute façon – ou presque).
Tout d’abord, rebelote mais en considérant les séries de numéros impairs. La méthode est la
même, les calculs sont de même nature mais les résultats diffèrent.
Reprenons d’abord l’équation (1), dans le cas où l’on s’intéresse aux séries de numéros
impairs :
et
On obtient alors la probabilité qu’une série de numéro impair soit de longueur k :

Puis on en calcule l’espérance, et on obtient :
De manière tout aussi surprenante que le résultat pour les séries de numéros pairs, la
longueur moyenne des séries de numéros impairs dépend elle de p, donc de si la pièce est truquée
ou équilibrée !
7) Et si l’on testait un peu tout ça ? ;)
Ces résultats semblant assez surprenants, pourquoi ne pas aller les vérifier après tout ? Ce
n’est pas à proprement parler une partie de la résolution du problème, mais ça m’amusait ;) Et c’est
intéressant aussi !
J’ai donc pris une pièce d’1$ néozélandais, et j’ai tiré à pile ou face 100 fois en notant à
chaque fois le côté qui sortait du jet. J’ai ensuite délimité les séries, compté leurs longueurs, et fait
les calculs de moyenne des longueurs. J’ai répété cela 20 fois.
Non je rigole, j’ai demandé à un ordinateur de le faire pour moi ! Ça permet de faire bien
plus de tirages pour une même séquence et de réaliser bien plus de séquences que n’importe qui en
aurait eu la patience ;) Enfin, ce n’est pas aussi simple que de le demander, il a fallu faire un peu de
programmation sous R (version 3.1.2). Mon script, que vous pouvez trouver à la fin de ce document,
n’est pas très élégant d’un point de vue de programmeur : il y a très certainement moyen
d’optimiser le nombre de lignes de codes, surtout quand j’utilise les mêmes boucles plusieurs fois, et
surtout j’insiste pour travailler avec des matrices, ce qui rajoute des lignes de code dont j’aurais sans
doute pu me passer ^^’ Mais je l’ai construit en suivant la logique de résolution de l’exercice (qui est
plus logique pour moi en tout cas).
Voici donc les résultats de cette expérience, pour différentes valeurs de p, volontairement
prises « en miroir » autour de ½ :
p = 1/5
p = 1/4
p = 1/3
p = 1/2
p = 2/3
p = 3/4
p = 4/5
2.023469
±
1.84187
2.193948
±
1.657151
2.025328
±
0.7422293
2.010931
±
0.3262646
1.996188
±
0.7961163
2.0018
±
1.219517
2.142271
±
1.602829
4.489319
±
1.739573
2.990809
±
1.03441
2.490302
±
0.8563335
2.024394
±
0.3489073
2.528058
±
0.8757788
3.446491
±
1.385318
3.960846
±
1.796049
En faisant mes petites manips sur R, je me suis aperçu qu’en fait ça valait le coup de calculer
les variances. Du moins de les faire calculer par R, et sans point de comparaison avec une valeur
donnée par le calcul (le calcul à la main des expressions de ces variances étant légèrement relou)…
De toute façon, R ne calcule pas directement une variance mais son estimateur sans biais (qui lui est
largement équivalent pour ce que je vais en faire ici). Et de toute façon bis, la variance (enfin, son
estimateur sans biais) ne sert qu’à illustrer qualitativement les phénomènes suivants : (1) les
variances de et augmentent lorsque p s’éloigne de ½ ; (2) ces conclusions se répètent « en
 6
6
 7
7
 8
8
 9
9
1
/
9
100%