Division euclidienne (rappels)

Division euclidienne (rappels)
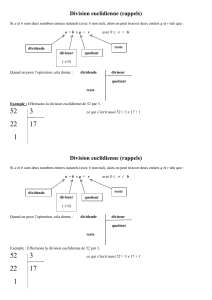
Si a et b sont deux nombres entiers naturels (avec b non nul), alors on peut trouver deux entiers q et r tels que :
a = b x q + r avec 0 ≤ r < b
Quand on pose l’opération, cela donne : dividende diviseur
quotient
reste
Exemple : Effectuons la division euclidienne de 52 par 3.
52 3 ce qui s’écrit aussi 52 = 3 x 17 + 1
22 17
1
Division euclidienne (rappels)
Si a et b sont deux nombres entiers naturels (avec b non nul), alors on peut trouver deux entiers q et r tels que :
a = b x q + r avec 0 ≤ r < b
Quand on pose l’opération, cela donne : dividende diviseur
quotient
reste
Exemple : Effectuons la division euclidienne de 52 par 3.
52 3 ce qui s’écrit aussi 52 = 3 x 17 + 1
22 17
1
dividende
diviseur
( ≠ 0)
quotient
reste
dividende
diviseur
( ≠ 0)
quotient
reste

Exercices sur la division euclidienne
Exercice 1 : Effectuer les divisions euclidiennes et vérifier les résultats à la calculatrice
138 5 192 6 369 3
138 = 5 x + 192 = 6 x + 369 = 3 x +
Par exemple, pour le premier, la suite de touches sur lesquelles il faut taper est : (sur la Casio fx-92)
138 5
Exercice 2 : 271 élèves d’un collège doivent participer à une course d’orientation. 30 adultes seront présents pour
encadrer cette sortie.
1/ Le déplacement doit s’effectuer dans des bus de 55 places maximum. Combien de bus faut-il ?
2/ Les professeurs décident de constituer le plus d’équipes possibles de 8 élèves. Combien d’équipes complètes feront-
ils ?
Exercice 3 : On a 12 croissants et 18 pains au chocolat que l’on veut répartir dans des corbeilles ayant toutes le même
contenu. Combien faut-il prévoir de corbeilles ? (Chercher toutes les possibilités)
Exercice 4 : Le célèbre pirate Edward Teach, dit « Barbe-noire », pille, en 1 718, un
navire chargé d’or. Il dit à ses 300 hommes : « Comptez ces pièces d’or. Partagez-les de
façon à ce que chacun en ait le même nombre et donnez-moi le reste ! » Le décompte
montre que le butin s’élève à 6 850 pièces d’or.
Que peut-on dire de ce partage ?
Exercice 5 : Madame Champ vient de recevoir un arrivage de 84 grandes marguerites et 48 roses. Elle souhaite répartir
toutes ces fleurs dans des bouquets identiques. (Tous les bouquets sont pareils)
1/ Peut-elle faire 7 bouquets ? 3 bouquets ? Si oui, quelle est alors la composition de chaque
bouquet ? (combien y a-t-il de roses, et combien y a-t-il de grandes marguerites ?)
2/ Ecrire la liste de tous les diviseurs de 48, puis la liste des diviseurs de 84. Entourer les
diviseurs communs aux deux listes.
3/ En déduire les nombres possibles de bouquets identiques que peut faire Madame Champ.
4/ En fait, elle veut réaliser le nombre maximal de bouquets identiques. Quel est ce nombre ?
Quelle est alors la composition de chaque bouquet ?
Le nombre trouvé dans la question 4 s’appelle le PGCD (plus grand des diviseurs communs) de 84 et 48.
Réponses partielles : exo 2 : 1/ 6 bus 2/ 33 équipes complètes exo 3 : 1 ; 2 ; 3 ou 6 corbeilles exo 5 : 4/ 12 bouquets de
7 grandes marguerites et 4 roses.

Fiche d’exercices récapitulative sur les nombres premiers
Exercice 1 : Le PGCD de deux entiers est le plus grand diviseur commun à ces deux entiers.
1/ Déterminer le PGCD de 15 et 25 en listant les diviseurs.
2/ Déterminer le PGCD de 17 et 81 en listant les diviseurs.
3/ Déterminer le PGCD de 910 et 105 à l’aide de l’algorithme d’Euclide.
4/ Déterminer le PGCD de 2 450 et 675 à l’aide de l’algorithme d’Euclide.
Exercice 2 : Numération binaire
Le système de numération binaire est un moyen de représenter les nombres avec deux symboles : 0 et 1.
Il est constamment utilisé en informatique.
Exemple : Le nombre 1 1 0 1 en écriture binaire correspond au nombre 13 en écriture décimale. On écrit :
= 8 + 4 + 0 + 1
= 13
1/ Trouver les nombres (en écriture décimale) correspondant aux nombres en écriture binaire
1 0 1 1 1 0 0 1 1 1 1 0 1
2/ On veut écrire 125 en écriture binaire :
 vérifier que la plus grande puissance de 2 contenue dans 125 est  donc 64 ;
 trouver le reste de la division euclidienne de 125 par 64, on peut alors écrire       ;
 trouver la plus grande puissance de 2 contenue dans 61 (le dernier reste), on peut alors écrire     ;
 recommencer le processus.
On peut alors écrire       et trouver ainsi son écriture en numération binaire.
3/ Trouver l’écriture binaire de 24 ; 36 ; 102
Exercice 3 : les ballons
1/ A la fin d’une fête de village, tous les enfants présents se partagent équitablement les 428
ballons de baudruche qui ont servi à la décoration. Il reste alors 37 ballons. Combien
pouvait-il y avoir d’enfants ?
2/ L’année suivante, ces mêmes enfants se partagent équitablement la totalité des 828 ballons
utilisés cette année là. Combien d’enfants étaient présents ?
Exercice 4 : Programme de calcul
« Je prends un nombre entier. Je lui ajoute 3 et je multiplie le résultat par 7. J’ajoute le triple du nombre de départ au
résultat et j’enlève 21. J’obtiens toujours un multiple de 10. »
Est-ce vrai ? Justifier.