Cours Cours

Chapitre 10 : Vitesse Moyenne
Chapitre 10 : Vitesse Moyenne
I]
I] Définition Définition
Définition
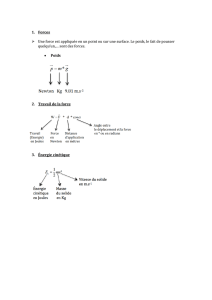
Définition Vitesse moyenne
La vitesse moyenne d'un mobile sur un parcours est le quotient de la distance parcourue par la
durée du parcours.
Exemple : Une tortue parcourt 500 mètres en 1 heure, elle avance à une vitesse moyenne de 500 m/h notée
aussi 500 m.h-1 (écriture scientifique).
II]
II] Unités de vitesse Unités de vitesse
Distance en ... m m km mm mm
Durée en ... s h h min s
Vitesse en ...
m.s-1
ou
m/s
m.h-1
ou
m/h
km.h-1
ou
km/h
mm.min-1
ou
mm/min
mm.s-1
ou
mm/s
Exemple :
Convertir une vitesse de 130 km.h-1 en m.s-1
v=130 km
1h
d = 130 km = 130 000 m
t = 1 h = 3 600 s
v=130000
3600 ≈36
m.s-1
➢Conversion de durées
Convertir 2,4 h en heures/minutes : t = 2,4 h = 2 h + 0,4 h
Durée (en h) 1 0,4
Durée (en min) 60 x = ?
L'égalité des produits en croix donne : x × 1 = 0,4 × 60. Donc, x = 24 min.
Donc, t = 2,4 h = 2 h 24 min.
Vitesse moyenne
Durée du parcours
Distance parcourue
v=d
t
1/3
On complète la 1ère colonne en utilisant les égalités de durée :
1 h = 60 min ; 1 min = 60 s ; 1 h = 3 600 s ; ….
Autre méthode :
En 1h, on parcourt 130 km.
En 3600 s, on parcourt 130 000 m.
En 1 s, on parcours 130 000/3 600 ≈ 36 m.
Donc, 130 km.h-1 ≈ 36 m.s-1.

Convertir 312 min en heures : t = 312 min = 5 × 60 min + 12 min = 5 h + 12 min
Durée (en h) 1 y = ?
Durée (en min) 60 12
III]
III] Calculs Calculs
➢Calcul de la vitesse
Une sortie scolaire est organisée en car pour aller au Futuroscope. Le départ se fait au collège à 6 h 00 et le
car arrive à destination à 11 h 00 après avoir parcouru une distance totale de 363 km.
Quelle était la vitesse moyenne du car ?
On sait que : t = 11 h 00 – 6 h 00 = 5 h ; d = 363 km ; v = ? (en km.h-1).
Or,
v=d
t
. Donc,
v=d
t=363 5=72,6
km.h-1 . Le car a roulé à une vitesse moyenne de 72,6 km.h-1.
➢Calcul de la distance :
Une voiture de course a roulé à 210 km.h-1 pendant 12 min.
Quelle distance a été parcourue pendant cette durée ?
On sait que : t = 12 min = 12 ÷ 60 h = 0,2 h ; v = 210 km.h-1 ; d = ? (en km)
Or,
v=d
t
. Donc,
210
1 = d 0,2
.
210
1 d 0,2
L'égalité des produits en croix donne :
d=210×0,2
1=42
km.
Cette voiture de course a donc parcouru 42 km.
➢Calcul de la durée :
Sarah court à une vitesse moyenne de 8 km.h-1.
Combien de temps mettra-t-elle pour faire une course de 3,8 km ?
On sait que : d = 3,8 km ; v = 8 km.h-1 ; t = ? (en h)
Or,
v=d
t
. Donc,
8
1=3,8 t
.
8
1 3,8 t
L'égalité des produits en croix donne :
t=3,8×1
8=0,475
h .
Donc, t = 0,475 × 60 min = 28,5 min = 28 min 30 s.
Sarah mettra 28 min 30 s pour terminer sa course.
L'égalité des produits en croix donne : y × 60 = 1 × 12.
Donc, x =12 ÷ 60 h = 0,2 h.
Donc, t = 5 h + 0,2 h = 5,2 h.
2/3

➢Trajet en plusieurs étapes
Ghislaine rend visite à son amie Léa. A l'aller, elle a mis 45 minutes pour parcourir les 30 km qui les séparent.
Au retour, elle n'a mis que 30 minutes.
(1) Déterminer sa vitesse moyenne VA à l'aller. (en km.h-1)
(2)Déterminer sa vitesse moyenne VR au retour. (en km.h-1)
(3) Déterminer sa vitesse moyenne V sur l'ensemble du trajet.
(1) On sait que : dA = 20 km ; tA = 30 min = 0,5 h
Or,
vA=dA
tA
. Donc,
vA=20
0,5
=40
km.h-1. A l'aller, sa vitesse moyenne était de 40 km.h-1.
(2) On sait que : dR = 20 km ; tR = 20 min = 1/3 h
Or,
vR=dR
tR
. Donc,
vR=20
1
3
=20×3
1
=60
km.h-1. Au retour, sa vitesse moyenne était de 60 km.h-1.
(3) On sait que : d = dA + dR = 20 km + 20 km = 40 km ; t = tA + tR = 0,5 h + 1/3h = 5/6h.
Or,
v=d
t
. Donc,
v=40
5
6
=40×6
5
=48
km.h-1.
Sur l'ensemble du trajet, sa vitesse moyenne était de 48 km.h-1.
Attention, sur un trajet en plusieurs étapes la vitesse moyenne de l'ensemble du trajet est obtenue
en divisant la distance TOTALE du trajet par la durée TOTALE du trajet.
Elle n'est généralement pas égale à la moyenne des vitesses sur chaque étape.
Exemple :
vA+vR
2=40+60 2=100 2=50
≠ 48.
!
3/3