Exercice 2 : Satellites

Exercice 1 : MOUVEMENTS PLANS
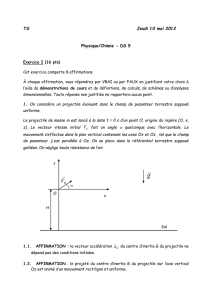
1. On considère un projectile évoluant dans le champ de pesanteur terrestre supposé uniforme.
Le projectile de masse m est lancé à la date t = 0 s d’un point O, origine du repère (O, x, z). Le vecteur

vitesse initial V 0 fait un angle  quelconque avec l’horizontale. Le mouvement s’effectue dans le plan

vertical contenant les axes Ox et Oz , tel que le champ de pesanteur g est parallèle à Oz. On se place dans
le référentiel terrestre supposé galiléen. On néglige toute résistance de l’air.
z

V0
O

g

x
H
Sol

1.1. AFFIRMATION : le vecteur accélération aG du centre d’inertie G du projectile ne dépend pas des
conditions initiales.
1.2. AFFIRMATION : le projeté du centre d’inertie G du projectile sur l’axe vertical Oz est animé d’un
mouvement rectiligne et uniforme.
1.3. AFFIRMATION : dans le cas où le projectile est lancé d’une hauteur H au dessus du sol avec une

2H
vitesse V 0 horizontale, l’abscisse de son point de chute est x = V0
g
On rappelle qu’à t = 0 s, le projectile est en O, origine du repère.
Exercice 2 : Satellites
Satellite
On considère un satellite artificiel soumis uniquement à la force
gravitationnelle de la Terre. Le satellite de masse m, situé à
l’altitude h par rapport au sol terrestre est animé d’un mouvement
circulaire et uniforme à la vitesse V. On se place dans le référentiel
géocentrique supposé galiléen.
On donne :
le rayon de la Terre :
RT = 6380 km
Terre
la masse de la Terre :
MT = 5,981024 kg
la constante de gravitation universelle :
G = 6,6710 -11 S.I.
h
RT
2.1. AFFIRMATION : la constante de gravitation universelle G s’exprime en m.s-2.

2.2. AFFIRMATION : le vecteur accélération aG du centre d’inertie du satellite est centripète.
2.3. AFFIRMATION : la vitesse du satellite est donnée par la relation V =
GM T
( RT  h)
2.4. AFFIRMATION : à l’altitude h = 12 800 km, la période de révolution du satellite vaut 2,64104 s
EXERCICE 3 : Energie dans un circuit RLC
On a réalisé le montage ci-dessous avec les composants suivants : un conducteur ohmique de résistance
R = 4,0102 , une bobine d’inductance L = 0,40 H (résistance interne de la bobine négligée) et un
condensateur de capacité C = 1,0. 10-6 F.
L
1
2
B
On charge le condensateur,
A
commutateur basculé en position
commutateur
1, puis, à l’instant de date t0 = 0, le
R
C
commutateur est basculé en E = 4,0 V
position 2.
i
M
Les points A, B et M sont reliés
à un ordinateur ou à un système
d’acquisition. Grâce à un
logiciel adapté on observe
l’évolution des tensions au
cours du temps (schéma ciaprès).
1. A propos des courbes
La courbe 1 visualisée est :
a. la tension aux bornes
du condensateur
b. la tension aux bornes
du conducteur ohmique
c. la tension aux bornes de la bobine
La courbe 2 visualisée est :
d. la tension aux bornes de la bobine
e. la tension aux bornes du conducteur ohmique
2. A propos des énergies
A l’instant initial le circuit RLC a emmagasiné une énergie E1 de :
a. 8,0 mJ
b. 8,0. 10-6 J
c. 2,0. 10-6 J
3. Lorsque les deux courbes se coupent pour la première fois, la valeur de l’intensité du courant vaut :
a. 5,0 mA;
b. 7,7 mA
c. 4,2 mA
4. Lorsque les deux courbes se coupent pour la première fois, la somme des énergies emmagasinée dans la
bobine et dans le condensateur notée E2 est :
a. 7,0. 10-6 J
b. 5,0. 10-6 J
c. 2,0. 10-6 J
5. Lorsque les deux courbes se coupent pour la première fois, l’énergie qui a été dissipée dans la résistance
vaut :
a. 3,0. 10-6 J
b. 1,0. 10-3 J
c. 10 mJ
On donne le graphe représentant en fonction du temps l’énergie cinétique et l’énergie potentielle élastique
d’un système solide–ressort horizontal, écarté de sa position d’équilibre, lâché sans vitesse initiale à l’instant
t = 0 s et à l’abscisse x0.
L’origine des abscisses correspond à la position d’équilibre du système.
1. La courbe correspondant à l’énergie cinétique est représentée en trait plein.
2. On suppose que l’énergie potentielle de pesanteur est nulle au niveau horizontal où se situe le
système. Le système de masse m, comporte un ressort de raideur k.
1
L’expression de l’énergie mécanique du système est donnée par l’expression : E m  kx02
2
3. L’allure des courbes permet d’affirmer qu’il n’y a pas de frottements.
EXERCICE 4 : énergie dans une pile
On dispose d’une solution de nitrate d’argent Ag+(aq) + NO3-(aq) de concentration 0,10 mol.L-1, d’une solution
de sulfate de cuivre de concentration 0,50 mol.L-1, d’un fil d’argent, d’une lame de cuivre et d’un pont salin
au nitrate de potassium.
On peut former une pile par l’association des couples Ag+(aq) / Ag(s) et Cu2+(aq) / Cu(s).
Soit l’équation de réaction :
2 Ag+(aq) + Cu(s) = 2 Ag(s) + Cu2+(aq)
La constante d’équilibre est K = 2,0.1015.
1. On relie les deux métaux constituant les bornes de la pile par une chaîne conductrice, le quotient de
réaction initial de ce système, pour l’équation donnée est :
a) Qr, i = 50, alors la réaction est spontanée dans le sens direct.
b) Qr, i = 50, alors la réaction est spontanée dans le sens inverse.
c) Qr, i = 0,02, alors la réaction est spontanée dans le sens direct.
d) Qr, i = 0,02, alors la réaction est spontanée dans le sens inverse.
2. Lorsque cette pile fonctionne (ou débite) son quotient de réaction :
a) augmente.
b) diminue.
c) ne varie pas.
3. Quel est le pôle négatif de la pile :
a) l’électrode d’argent ?
b) l’électrode de cuivre ?
Une pile de ce type a une f.é.m. E = 2,0 V ; elle est prévue pour fonctionner pendant 10 h si elle débite de
manière constante un courant d’intensité 320 mA.
Données :
1 F = 9,65.104 C.mol-1
1. L’énergie maximale disponible de cette pile est égale à :
a) 11,5 J ;
b) 1,15.104 J ;
c) 2,30.104 J.
2. La quantité d’électrons qui circulent pendant la durée totale du fonctionnement est égale à :
a) 0,12 mol ;
b) 1,0 mol ;
c) 2,0 mol.
Exercice 5 Propagation d'une onde.
 On fixe un vibreur à l'extrémité d'une corde tendue. Une onde sinusoïdale de fréquence f = 25 Hz se
propage le long de la corde. Le milieu n'est pas dispersif.
Affirmation 1 : l'onde est transversale.
Affirmation 2 : la célérité de l'onde est v = 20 m.s-1.
Affirmation 3 : la célérité de l'onde dépend de la fréquence de la source.
Affirmation 4 : au moment de la prise de vue, le point M descend.
 Dans un milieu non dispersif, une onde rectiligne sinusoïdale traverse une fente dont la largeur, fixe, est de
l'ordre de grandeur de la longueur d'onde.
Affirmation 5 : le phénomène de diffraction est d'autant plus marqué que la fréquence de l'onde est grande.
Exercice 6 Radioactivité.
 Le graphe ci-contre (figure 2) représente l'évolution
temporelle de l'activité A d'un échantillon de radon
222.
Affirmation 6 : la demi-vie du radon 222 est :
t1/2 = 5,5 jours
Affirmation 7 : à l'instant de date t = 1,0 jour, il reste
environ 2,4  108 noyaux de radon 222 dans
l'échantillon.
Exercice 7 Évolution des systèmes électriques RC et RL
• La résistance du circuit de la figure 3 est réglable. Le générateur
délivre une tension constante E = 6,0 V. Le condensateur a une capacité
C = 1,0 µF
Un système d'acquisition permet d'enregistrer l'évolution
de la tension aux bornes du condensateur en fonction du
temps (figure 4).
À l'instant de date t = 0 s, on ferme l'interrupteur.
Affirmation 8 : à l'instant de date t = 0 s, le
condensateur est déchargé.
Affirmation 9 : en régime permanent l'intensité du
courant qui circule dans le circuit est nulle.
Affirmation 10 : pour obtenir la courbe 1, il faut donner à la résistance la valeur R = 2,0 k.
Affirmation 11 : pour passer de la courbe 1 à la courbe 2, il suffit de diminuer la valeur de la résistance.
• La résistance du circuit de la figure 5 est réglable. Le générateur
délivre une tension constante E = 6,0 V. La bobine a une résistance
interne négligeable devant R et une inductance L.
Un système d'acquisition permet d'enregistrer l'évolution au cours du
temps de l'une des tensions indiquées sur le schéma.
A l'instant de date t = 0 s, on ferme l'interrupteur.
Affirmation 12 : l'intensité du courant qui circule dans le
L di
E
circuit vérifie l'équation différentielle : i –
R dt
Affirmation 13 : la courbe de la figure 6 représente la
tension aux bornes du conducteur ohmique.
Exercice 8. Évolution des systèmes chimiques.
• La courbe l de la figure 7 représente
l'évolution au cours du temps de l'avancement
de la réaction entre une mole d'acide
éthanoïque et une mole d'éthanol à
100°C sans catalyseur. La réaction conduit
à un équilibre chimique.
Affirmation 14 : à l'instant de date t = 0 h,
la vitesse de la réaction est nulle.
Affirmation 15 : une élévation de température
du
milieu
réactionnel
modifie
la vitesse de réaction.
Affirmation 16 : la vitesse de la réaction
diminue au cours du temps.
Affirmation 17 : l'ajout d'un catalyseur
dans le milieu réactionnel permet d'obtenir
la courbe 2.
 On étudie la réaction d'oxydation de
l'acide oxalique HOOC-COOH (solution
incolore)
par
l'ion
permanganate
MnO 4 (aq) en milieu acide (solution de
couleur violette). Le suivi de la réaction
est
réalisé par
un enregistrement
spectrophotométrique. La transformation
est totale. Parmi tous les réactifs et
produits
présents
dans
le
milieu
réactionnel, seul l'ion permanganate est
coloré et absorbe à la longueur d'onde
choisie. L'évolution de l'absorbance du
milieu réactionnel en fonction du temps est donnée sur le graphe ci-contre (figure 8).
Affirmation 18 : l'ion permanganate n'est pas le réactif limitant.
Exercice 9 : piles
 On réalise une pile avec les couples Fe3+(aq)/Fe2+(aq) et Ag+(aq)/Ag(s) (voir schéma de la figure 9).
La constante d'équilibre associée à la réaction (1) ci-dessous :
Fe3+(aq) +Ag(s) = Fe2+(aq) + Ag+(aq) vaut K = 0,31
Tous les ions en solution ont initialement la même
concentration :
[Fe2+(aq)] ini = [Fe3+(aq)]ini = [Ag+(aq)] ini = 0,20 mol.L–1
Affirmation 19 : quand le courant circule dans le circuit
extérieur, la transformation qui s'effectue dans la pile est une
transformation forcée.
Affirmation 20 : le sens spontané d'évolution de la réaction
(1) est le sens direct.
Affirmation 21 : en multipliant par 2 la concentration initiale des ions Ag+(aq) sans changer les autres
concentrations, on inverse le sens d'évolution de la réaction (1).
Exercice 10 : Toute la chimie
1  Autoprotolyse de l’eau.
1.1. L’équation de la réaction d’autoprotolyse de l’eau est :
1.1.1. H3O+ + HO = 2 H2O
1.1.2. H2O + H2O = H3O+ + HO
1.1.3. 2 H2O + 2 e = H2 + 2 HO
Aucune justification demandée
1.2. La constante d’équilibre associée à l’équation de la réaction d’autoprotolyse de l’eau est appelée :
1.2.1. le produit de solubilité de l’eau.
1.2.2. le quotient de réaction de l’eau.
1.2.3. le produit ionique de l’eau.
Aucune justification demandée
1.3. On peut également interpréter cette constante d’équilibre comme :
1.3.1. la constante d’acidité du couple H2O / HO.
1.3.2. la constante d’acidité du couple H3O+/ H2O.
1.3.3. la constante d’acidité du couple H3O+/ HO.
2  On met en présence 0,6 mole d’acide
carboxylique et 0,6 mole d’alcool puis,
sans intervenir en aucune façon, on
laisse évoluer le mélange maintenu à
une température T constante.
Le suivi cinétique de la transformation
qui se déroule a permis de tracer les
courbes 1 et 2, représentant l’évolution
de l’avancement x au cours du temps :
2.1. La vitesse volumique de réaction :
2.1.1. est nulle à l’instant de date t = 0 s.
2.1.2. est maximale à l’instant de date t = 0 s.
2.1.3. est exprimée en mol.min1.
2.2. La courbe 3 :
2.2.1. peut être obtenue en réalisant la transformation à une température T3 supérieure à T2.
2.2.2. peut être obtenue en réalisant la transformation à une température T3 supérieure à T2 et en
présence d’un catalyseur.
2.2.3. ne peut pas être obtenue dans les conditions décrites.
2.3. L’ester obtenu a pour formule semi-développée :
O
HC
Son nom est :
2.3.1. le propanoate de méthyle.
2.3.2. le méthanoate de propanyle.
2.3.3. le méthanoate de propyle.
O  (CH2)2  CH3
Aucune justification demandée
3  À une transformation chimique est associée la réaction d’équation : 2 A + B = 2 C + 3 D où les espèces
chimiques A, B, C et D n’ont pas besoin d’être précisées.
Les mesures ont permis d’établir le tableau d’avancement suivant :
État initial
État final
Avancement
0
xfinal
2A
0,40
0,30
+
3.1. Le taux d’avancement final de cette transformation est :
3.1.1.  = 0,25
3.1.2.  = 0,50
B
0,30
0,25
=
2C
0
0,10
+
3D
0
0,15
3.1.3.  = 0,75
3.2. Dans les conditions de l’expérience, la constante d’équilibre K associée à cette équation est
K = 1,08
Cette valeur :
3.2.1. dépend de la composition initiale du système.
3.2.2. dépend de la composition initiale du système et de la température.
3.2.3. dépend de la température.
Aucune justification demandée
3.3. Le taux d’avancement final de la transformation :
3.3.1. dépend à la fois de la constante d’équilibre K et de la composition initiale du système.
3.3.2. ne dépend que de la composition initiale du système.
3.3.3. ne dépend que de la constante d’équilibre K.
Aucune justification demandée
4  On considère un acide noté AH. Lors de la préparation d’une solution aqueuse, la transformation de
cet acide avec l’eau est quasi totale. On titre cette solution par une solution aqueuse d’hydroxyde de
sodium de concentration molaire en soluté apporté connue.
4.1. L’équation de la réaction de titrage est :
4.1.1. AH + HO = H2O + A
4.1.2. H3O+ + HO = 2 H2O
4.1.3. A + H3O+ = AH + H2O
4.2. Le suivi pH-métrique de
ce titrage a permis d’obtenir
la courbe ci-contre :
Pour réaliser un suivi colorimétrique de ce titrage (voir données page suivante) :
4.2.1. seul le bleu de bromothymol convient.
4.2.2. le bleu de bromothymol et le rouge de crésol conviennent.
4.2.3. le bleu de bromothymol, le rouge de crésol et le bleu de bromophénol conviennent.
Données :
Indicateur coloré
bleu de bromophénol
bleu de bromothymol
rouge de crésol
Teinte acide
jaune
jaune
jaune
Zone de virage
3,0  4,6
6,0  7,6
7,2  8,8
Teinte basique
bleu
bleu
rouge
5  On réalise le montage suivant Générateur
:
de tension
+
5.1. Ce montage permet de réaliser :
5.1.1. une pile.
5.1.2. une électrolyse.
5.1.3. une transformation spontanée.

Lames de plomb
Seul le couple Pb2+/ Pb intervient.


Solution aqueuse d'éthanoate de plomb ( Pb(2aq
)  2CH 3COO( aq ) ) acidifiée.
5.2. Au bout de quelques minutes, on observe :

5.2.1. +
5.2.2. +

5.2.3.
+

dégagement gazeux
6  On considère


 une solution aqueuse S1 de nitrate de plomb (II) : ( Pb(2aq
) + 2 NO3( aq ) ) telle que

 3 mol.L1
[ Pb(2aq
) ] =1,0 × 10


 une solution aqueuse S2 de chlorure de fer (II) : ( Fe(2aq
) + 2 Cl( aq ) ) telle que

2
[ Fe(2aq
mol.L1
) ] = 4,0 × 10

2
La constante d’équilibre K associée à la réaction d’équation : Pb(2aq
) + Fe(s) = Pb(s) + Fe( aq ) vaut
3,0 × 1010.
6.1. Une pile est constituée des deux demi-piles suivantes, reliées par un pont salin :
 une lame de plomb plongeant dans la solution S1
 une lame de fer plongeant dans la solution S2
On la branche aux bornes d’un conducteur ohmique de résistance R = 100 .
Après une durée de fonctionnement de 30 minutes :
6.1.1. la masse de la lame de fer a augmenté.
6.1.2. la masse de la lame de fer a diminué.
6.1.3. la valeur de la résistance R n’a aucune influence sur la variation de masse des lames.
6.2. Dans un bécher, on plonge une lame de plomb dans un mélange de 20 mL de la solution S1 et de
20 mL de la solution S2 :
6.2.1. le système n’évoluera pas.
6.2.2. on observera la formation d’un dépôt de fer sur la lame de plomb.
6.2.3. la masse de la lame de plomb va augmenter.
Exercice 11 : chimie organique
Le chimiste français T.J. Pelouze fût le premier, au XIX ème siècle, à décrire la synthèse d’un
triglycéride : la butyrine (notée E dans tout l’exercice), principal constituant du beurre.
Le texte ci-dessous est inspiré de son mémoire, paru dans les Annales de Chimie et Physique, en
1844 :
L’acide butyrique (ou acide butanoïque) a été découvert en 1814, parmi les produits de la
saponification du beurre, par M. Chevreul, qui en a décrit l’histoire avec beaucoup de soin dans son
ouvrage sur les corps gras d’origine animale. […]
Nous nous bornerons aujourd’hui à présenter quelques observations relatives à l’action de l’acide
butyrique sur la glycérine.
(1) Lorsqu’on chauffe légèrement un mélange de ces deux substances et d’acide sulfurique concentré
et qu’on le verse ensuite dans une grande quantité d’eau, on voit aussitôt se séparer de la solution
aqueuse une huile liquide légèrement jaunâtre notée (E). On peut laver cette huile avec de grandes
quantités d’eau car elle est peu soluble dans l’eau.
(2) Si on mélange à chaud cette matière grasse (E) avec une solution concentrée de potasse
caustique, on en retire du butanoate de potassium et de la glycérine
Données :
La potasse caustique est une solution aqueuse d’hydroxyde de potassium (K + + HO –)
Masse molaire de la butyrine : M1 = 302 g.mol –1
Masse molaire du butanoate de potassium : M2 = 126 g.mol –1
Acide
Nom du
butanoïque
Glycérine
Butyrine (E)
composé
(Acide
butyrique)
O
CH3
Formule semidéveloppée
CH3
CH2
H2C
OH
HC
OH
H2C
OH
CH2
C
CH2
CH2
CH3
CH2
CH22
C
O
O
CH
CH3
CH2
CH2
C
O
CH2
1. La réaction associée à la transformation décrite en (1) est une :
a. estérification
b. hydrolyse
2. La transformation décrite dans l’étape (1) est :
a. limitée
b. rapide.
3. Lors de la transformation décrite dans l’étape (1), l’acide sulfurique joue le rôle de :
a. solvant
b. réactif
c. catalyseur.
4. Le chauffage utilisé dans l’étape (1) permet de :
a. homogénéiser le milieu réactionnel
O
O
O
OH
C
b. augmenter le rendement
c. accélérer la transformation
5. Pour séparer l’huile obtenue dans l’étape (1) de la solution aqueuse, on peut utiliser :
a. une filtration sur Büchner
b. une ampoule à décanter
c. une filtration sur papier filtre.
6. La transformation citée dans l’étape (2) est une :
a. estérification
b. hydrolyse basique d’un ester
c. réaction acide-base
d. saponification
7. L’ion butanoate obtenu lors de l’étape décrite en (2) possède :
a. une partie hydrophobe
b. une partie anhydre
c. une partie hydrophile
8. La réaction associée à la transformation citée dans l’étape (2) a pour équation :
(E) + 3K+(aq) + 3HO –(aq) = 3K+(aq) + 3CH3(CH2)2COO –(aq) + CH2OH CHOH CH2OH( )
8.1. On mélange 15 g de butyrine avec 0,15 mol d’hydroxyde de potassium.
Les réactifs sont introduits dans les proportions :
a. stœchiométriques
b. non stœchiométriques : la butyrine est en excès
c. non stœchiométriques : la potasse est en excès
8.2. On obtient une masse m = 6,3 g de butanoate de potassium.
Le rendement de la réaction est :
a. 33%
b. 50%
c. 99%