+ ln

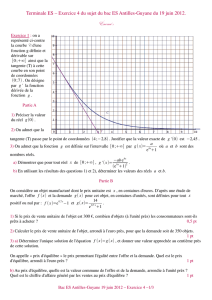
Terminale ES
La fonction logarithme
népérien
1

TES La fonction logarithme népérien
La fonction logarithme népérien
La fonction logarithme népérien, notée ln, est la fonction définie sur
]0; + [, qui à tout nombre réel x > 0 associe l’unique solution de
l’équation ey = x d’inconnue y.
On note cette solution y = ln x.
Définition
2
I Liens avec la fonction exponentielle
On sait que la fonction exponentielle est strictement croissante sur  et à
valeurs dans ]0;+ [.
Ainsi, pour tout nombre réel a > 0, il existe un unique nombre réel b tel que eb = a.

TES La fonction logarithme népérien
La fonction logarithme népérien
3
II Conséquences
Les propriétés suivantes découlent directement de la définition :
1. Pour tous réels x > 0 et y, ex = y  x = ln y.
2. Pour tout réel x > 0, eln x = x.
3. Pour tout réel x, ln(ex) = x.
4. ln 1 = 0 (car e0 = 1) ln e = 1 (car e = e1) ln 
 = -1 (car   = e-1)
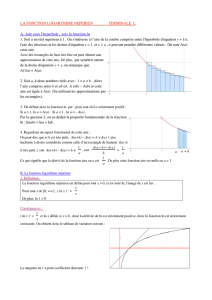
III Courbe représentative de la fonction ln
Dans un repère orthonormé, les courbes
représentatives des fonctions exponentielle et
logarithme népérien sont symétriques par rapport
à la droite  d’équation y = x.
Propriété

TES La fonction logarithme népérien
La fonction logarithme népérien
4
La fonction logarithme népérien est continue et dérivable sur ]0; + [.
Propriété

TES La fonction logarithme népérien
Etude de la fonction ln
5
IV Fonction dérivée de ln
Pour tout nombre réel x > 0, ln’(x) = 
.
Propriété
Démonstration
On note f la fonction définie sur ]0; + [ par f(x) = eln x.
Cette fonction est de la forme eu avec u(x) = ln x.
La fonction ln étant dérivable sur ]0; + [ alors la fonction f est aussi dérivable
sur ]0; + [.
Pour tout réel x > 0, f’(x) = u’(x)eu(x) = u’(x) f(x).
Or f(x) = x et f’(x) = 1
Donc u’(x) = ln’(x) = 