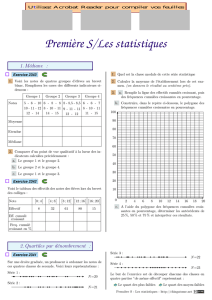
STATISTIQUES DESCRIPTIVES Plan du cours : — Généralités

STATISTIQUES
DESCRIPTIVES
Plan du cours :
—G´en´eralit´es
— Variables qualitatives
— Variables quantitatives
Discr`etes
Continues
Repr´esentation,
Caract´eristiques
— Distributions bivari´ees

Chapitre 1
G´en´eralit´es
1. Introduction
2. Type de variable
1 Introduction
LetermeStatistiqueenglobeunensembledem´ethodes
scientifiques bas´ees sur des donn´ees (num´eriques ou non)
recueillies sur une population pour d´ecrire et analyser cette
population.
Vocabulaire
— Population : ensemble d’objets de mˆeme nature.
— Individu : ´el´ement de cette population.
—Effectif total N: nombre d’individus de la population.
— Variable ou Caract`ere X:caract´eristique ´etudi´ee sur la
population, recueillie pour chaque individu.

Postulat : On suppose que la variable est soumise `aune
grande variabilit´e due `a de nombreux facteurs inconnus ou
au hasard.
Exemple :
—Population:
´
Etudiants de premi`ere ann´ee de licence Sci-
ences Humaines de Paris X.
— Individu : Un ´etudiant de premi`ere ann´ee de licence Sci-
ences Humaines de Paris X.
—Variables:
S´erie du baccalaur´eat
Age
Nombre de fr`eres et soeurs
Note en psycho au premier semestre
Dur´ee du trajet domicile-universit´e
.....

Statistique Descriptive : ensemble de m´ethodes bas´ees sur
l’organisation des donn´ees pour repr´esenter graphiquement
et r´esumer num´eriquement les donn´ees dans le but de d´ecrire
et d’analyser la population.
→Repr´esentations graphiques
→R´esum´es num´eriques (si possible) : on synth´etise les
donn´ees par des param`etres num´eriques pour d´ecrire la
population, et ´eventuellement comparer celle-ci avec une
autre population.

2Typedevariable
On distingue les variables selon qu’elles prennent des valeurs
num´eriques ou non. On dit qu’une variable est
—qualitative si ses valeurs sont des cat´egories qu’on ap-
pelera “modalit´es”
-nominale ou cat´egorielle,s’iln’existeaucunerelation
entre les modalit´es prises par la variable
-ordinale, s’il existe une relation d’ordre entre les modalit´e
s
prises par la variable
—quantitative si elle prend des valeurs num´eriques
-discr`ete lorsqu’elle prend un nombre fini de valeurs
(souvent enti`eres).
-continue lorsqu’elle prend des valeurs r´eelles.
qualitative quantitative
nominale ordinale discr`ete continue