Correction des exercices sur la conservation de l`énergie

correction Première S EABJM
S.COUTRY correction des exercices sur le travail et l’énergie Page 1 sur 6
Correction des exercices sur la conservation de l’énergie
Exercice 1: pendule simple:
1. La somme E
c
+ E
pp
se conserve:
Le système {bille S} est soumis à 2 forces extérieures:
• Son poids .
• La tension du fil .
Comme les frottements sont négligés, il n’y a pas de perte d’énergie sous forme thermique. Toute l’énergie
potentiel de pesanteur se transforme en énergie cinétique et vis-versa. .
La somme Ec + Ep se conserve donc.
A l'instant initial (instant 1)
Energie cinétique:
Ec
1
= 1/2.m.V
1
2
.
Energie potentielle de pesanteur:
Ep
1
= m.g.h
1
avec h
1
=L.(1-cos(
θ
1
)), d'où:
Ep
1
= m.g.L.(1-cos(
θ
1
))
Somme E
c
+ E
pp
Ec
1
+ Ep
1
= 1/2.m.V
1
2
+ m.g.L.(1-cos(q
1
))
2. Angle maximum de remontée:
A l'instant final (instant 2)
Énergie cinétique:
Ec
2
= 0.
Energie potentielle de pesanteur:
Ep
2
= m.g.h
2
avec h
2
=L.(1-cos(
θ
m
)), d'où:
Ep
2
= m.g.L.(1-cos(
θ
m
))
Somme E
c
+ E
pp

correction Première S EABJM
S.COUTRY correction des exercices sur le travail et l’énergie Page 2 sur 6
Ec
2
+ Ep
2
= m.g.L.(1-cos(
θ
m
))
La somme Ec + Ep se conserve, donc:
1/2.m.V
12
+ m.g.L.(1-cos(θ
1
)) = m.g.L.(1-cos(θ
m
))
1/2.V
12
+ g.L - g.L.cos(θ
1
) = g.L - g.L.cos(θ
m
)
V
12
-2.g.L.cos(θ
1
) = -2.g.L.cos(θ
m
)
cos(θ
m
) =
2.g.L.cos(
θ
1
) - V
1
2
2.g.L
cos(θ
m
) =
2 x 9,81 x 0,80 x cos(30) - 1,5
2
2 x 9,81 x 0,80
cos(θ
m
) = 0,72
θ
m
= 44°.
Mouvement ultérieur du pendule:
La somme Ec + Ep se conserve. Le pendule ne perd pas d'énergie et le pendule va osciller indéfiniment entre
les angles +q
m
et -q
m
.
3. Vitesse V
1
':
A l'instant initial:
Énergie cinétique: Ec
1
= 1/2.m.V
1
'
2
.
Énergie potentielle: Ep
1
= m.g.L.(1-cos(θ
1
))
On en déduit: Ec
1
+ Ep
1
= 1/2.m.V
1
'
2
+ m.g.L.(1-cos(θ
1
))
Énergie mécanique finale:
Énergie cinétique: 1/2.m.V
22
.
Énergie potentielle: Ep
2
= 2.m.g.L (le pendule est à la verticale).
On en déduit: E
c2
+ E
pp2
= 1/2.m.V
22
+ 2.m.g.L
La somme Ec + Ep se conserve, donc:
Ec
1
+ Ep
1
= Ec
2
+ Ep
2
1/2.m.V
1
'
2
+ m.g.L.(1-cos(θ
1
)) = 1/2.m.V
22
+ 2.m.g.L
V
1
'
2
+ 2.g.L.(1-cos(θ
1
)) = V
22
+ 4.g.L

correction Première S EABJM
S.COUTRY correction des exercices sur le travail et l’énergie Page 3 sur 6
V
1
'
2
+ 2.g.L. - 2.g.L.cos(θ
1
) = V
22
+ 4.g.L
V
1
'
2
= V
22
+ 2.g.L + 2.g.L.cos(θ
1
))
V
1
'
2
= V
22
+ 2.g.L.(1 + cos(θ
1
))
V
1
'
2
= 5,0
2
+ 2 x 9,81 x 0,80.(1 + cos(30))
V
1
'
2
= 54,3m
2
.s
-2
V
1
' = 7,4m.s
-1
.
Exercice 2: tir d'un projectile:
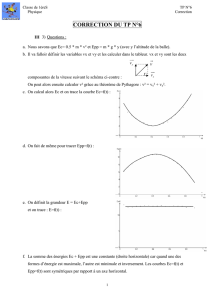
1. Coordonnées du vecteur vitesse initiale:
2. Expression de l'altitude Zs du sommet S de
la trajectoire:
.
Le système {pierre} n'est soumis qu'à son poids
La somme E
c
+ E
pp
(énergie cinétique + énergie
potentielle de pesanteur) se conserve car les
frottements sont négligés.
Au point O:
Énergie cinétique: E
c
(O) = 1/2.m.V
o2
.
Énergie potentielle: E
pp
(O) = 0.
D'où E
c
(O) + E
pp
(O) = 1/2.m.V
o2
. Au point S (sommet de la trajectoire):
Énergie cinétique: E
c
(S) = 1/2.m.V
s2
.
Énergie potentielle: E
pp
(S) = m.g.z
s
.
D'où E
c
(O) + E
pp
(O) = 1/2.m.V
s2
+ m.g.z
s
.
La somme E
c
+ E
pp
se conserve, donc:
E
c
(O) + E
pp
(O) = E
c
(S) + E
pp
(S) =
1/2.m.V
o2
= 1/2.m.V
s2
+ m.g.z
s
V
o2
= V
s2
+ 2.g.z
s
Or V
s
= V
ox
= V
o
.cos( α ), d'où:
V
o2
= V
o2
.cos
2
( α ) + 2.g.z
s
2.g.z
s
= V
o2
.(1 - cos
2
( α ))
z
s
=
V
o
2
.(1-cos
2
( α ))
2.g
3. application numérique:
Pour a = 30,0°:
z
s
=
15,0
2
x (1 - cos
2
(30,0))
2 x 9,81
z
s
= 2,87 m.
Pour α = 60,0°:
z
s
= 8,60 m.
Il est immédiat que:
V
ox
= V
o
.cos(
α
)
V
oz
= V
o
.sin(α)

correction Première S EABJM
S.COUTRY correction des exercices sur le travail et l’énergie Page 4 sur 6
4. Vitesse au point d'impact avec le sol:
Au point O:
Énergie cinétique: E
c
(O) = 1/2.m.V
o2
.
Énergie potentielle: E
pp
(O) = 0.
D'où E
c
(O) + E
pp
(O) = 1/2.m.V
o2
.
Au point D:
Énergie cinétique: E
c
(D) = 1/2.m.V
D2
.
Énergie potentielle: E
pp
(D) = 0.
D'où E
c
(D) + E
pp
(D) = 1/2.m.V
D2
.
La somme E
c
+ E
pp
se conserve, donc:
Em
O
= Em
D
1/2.m.V
o2
= 1/2.m.V
D2
V
o2
= V
D2
V
o
= V
D
La vitesse au point D est V
D
= 15,0m.s
-1
.
Remarque: Vecteur vitesse au point D: voir schéma (le vecteur vitesse est tangent à la trajectoire au point D).
Exercice 3: la boutique de l’homme fort:
1. Référentiel, origine des espaces, origine des énergies:

correction Première S EABJM
S.COUTRY correction des exercices sur le travail et l’énergie Page 5 sur 6
2. Distance parcourue par le palet:
Au point A
Énergie cinétique: E
c
(A) = 1/2.m.V
o2
.
Énergie potentielle: E
pp
(A) = m.g.y
A
.
D'où E
c
(A) + E
pp
(A) = 1/2.m.V
o2
+ m.g.y
A
.
Au point B (endroit de l'arrêt)
Énergie cinétique: E
c
(B) = 0.
Énergie potentielle: E
pp
(B) = m.g.y
B
.
D'où E
c
(B) + E
pp
(B) = m.g.y
B
.
D'autre part, le palet est soumis à 2 forces extérieures:
• Son poids .
• La réaction du support du plan incliné.
W
AB
( )=0 car et la somme E
c
+ E
pp
(énergie cinétique + énergie potentielle de pesanteur) se conserve
car toutes les forces extérieures (sauf le poids) effectuent un travail nul.
E
c
(A) + E
pp
(A) = E
c
(B) + E
pp
(B)
=>
1
/
2
.m.V
o
2
+ m.g.y
A
= m.g.y
B
=>
V
o
2
= 2.g.(y
B
- y
A
)