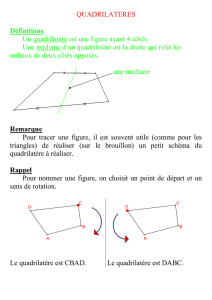
définition

—
©
Cned, Mathématiques 6e
18
c
c
Séquence 7
Séance 4
Ce que tu devais faire Les commentaires du professeur
Exercice 25
# .
"6
CM
CM
Les commentaires du professeur :
• On commence par construire avec l’équerre et la règle graduée les deux côtés perpendiculaires [CN]
# .
"
CM
CM
et [NB] tels que : NC = 5 cm et NB = 3 cm.
• On trace la demi-droite [Cx) perpendiculaire en C à la droite (CN) puis la demi-droite [By)
C N
B
5 CM
3 CM
x
y
V
perpendiculaire en B à la droite (BN). Le point V est le point commun à ces deux demi-droites.
• À l’aide de l’équerre, on peut vérifier que l’angle
CVB
∑
semble droit. On verra par la suite à l’aide d’une démonstration que cet
angle est un angle droit.
Tu as déjà rencontré un tel quadrilatère : on l’appelle un rectangle.
Exercice 26
définition
définition
définition
définition
5N RECTANGLE EST UN
quadrilatère QUI A QUATRE
ANGLESdroits
2%#4!.',%
On recopie simplement les mots qui manquent
dans la carte en prenant modèle sur le
paragraphe « JE RETIENS » précédent.
© Cned – Académie en ligne

©
Cned, Mathématiques 6e —
19
c
c
Séquence 7
Exercice 27
1)
Les droites (DH) et (FG) sont toutes les
deux perpendiculaires à la droite (DF).
Les droites (DH) et (FG) sont donc
parallèles.
$(
&'
2)
On vient de démontrer que les droites
(DH) et (FG) sont parallèles.
La droite (GH) est perpendiculaire à la
droite (DH), elle est donc perpendiculaire
à la droite (FG).
$ (
& '
3) Le quadrilatère DFGH possède donc en fait 4 angles droits.
Par définition, c’est donc un rectangle.
4) On a démontré dans le 2) que ses côtés opposés [DH] et
[FG] sont parallèles. De même, les côtés opposés [DF] et [HG]
sont parallèles parce qu’ils sont tous les deux perpendiculaires
au côté [DH].
1) On utilise la propriété 1 du paragraphe
« JE RETIENS » de la séquence 1 séance 7.
2) On utilise la propriété 2 du paragraphe
« JE RETIENS » de la séquence 1 séance 8.
3) En conclusion, dès qu’un quadrilatère
possède trois angles droits, son quatrième
angle est droit également : ce quadrilatère est
donc un rectangle.
Exercice 28
2%#4!.',%
reconnaître
3I UN QUADRILATÒRE A trois
ANGLES DROITS ALORS CgEST UN
rectangle
On recopie simplement les mots qui manquent
dans la carte en prenant modèle sur le
paragraphe « JE RETIENS » précédent.
Exercice 29
+D
Dg
.
,
-
+D
Dg
.
,-
+D .
,
+
,-
Les axes de symétrie du rectangle sont les droites (d) et (d’).
On plie soigneusement de façon à faire une
bonne observation.
Seuls les pliages suivant les droites (d) et
(d’) permettent d’obtenir que les sommets,
les côtés et les angles du rectangle KLMN se
superposent exactement. Ce sont les deux
seuls axes de symétrie du rectangle.
© Cned – Académie en ligne

—
©
Cned, Mathématiques 6e
20
c
c
Séquence 7
Exercice 30
2%#4!.',%
propriété
propriété
propriété
propriété
propriété
3IUNQUADRILATÒREESTUNRECTAN
GLEALORSILADMETdeuxAXESDE
SYMÏTRIE  LES médiatrices DE
DEUXCÙTÏSCONSÏCUTIFS
On recopie simplement les mots qui manquent
dans la carte en prenant modèle sur le
paragraphe « JE RETIENS » précédent.
Exercice 31
1)
a) Quel est le symétrique du segment [AD] par rapport à la
droite (d) ? [BC].
Que peux-tu en déduire concernant les longueurs des segments
[AD] et [BC] ? Elles sont égales.
b) Quel est le symétrique du segment [AB] par rapport à la
droite (d’) ? [DC].
Que peux-tu en déduire concernant les longueurs des segments
[AB] et [DC] ? Elles sont égales.
c) Quelle propriété viens-tu de démontrer ?
Si un quadrilatère est un rectangle, alors ses côtés opposés
sont de même longueur.
2)
!
I
" #
$
D
Dg
a) Quel est le point d’intersection de ces diagonales ? le point I
b) Quel est le symétrique du segment [AC] par rapport à la
droite (d’) ? [DB]
Que peux-tu en déduire concernant les longueurs des segments
[AC] et [BD] ? Elles sont égales.
c) Quelle propriété viens-tu de démontrer ?
Si un quadrilatère est un rectangle, alors ses diagonales sont
de même longueur.
3)
a)
En utilisant la symétrie par rapport à la droite (d’), compare les
distances IA et ID : IA =ID
En utilisant la symétrie par rapport à la droite (d), compare les
distances ID et IC : ID =IC
En utilisant la symétrie par rapport à la droite (d’), compare les
distances IC et IB : IC = IB
En utilisant la symétrie par rapport à la droite (d), compare les
distances IB et IA : IB = IA
b) Compare IA et IC : IA = IC puis IB et ID : IB = ID
Le point I est le milieu des diagonales [AC] et [BD].
c) Si un quadrilatère est un rectangle, alors ses diagonales ont
le même milieu.
1) a) par la symétrie par rapport à la droite
(d) :
A a pour symétrique B
D a pour symétrique C.
[AD] a donc pour symétrique [BC].
On utilise la propriété de la symétrie suivante
« un segment et son symétrique ont la même
longueur ».
b) Par la symétrie par rapport à la droite (d’) :
A a pour symétrique D
B a pour symétrique C.
[AB] a donc pour symétrique [DC].
c) C’est une propriété importante que l’on
devra retenir.
2) b) par rapport à la droite (d’) :
Le symétrique de A est D.
Le symétrique de C est B
Donc :
Le symétrique de [AC] est [DB].
c) N’oublie pas que les segments [AC] et
[BD] sont les diagonales.
3) a)
• En effet, [IA] et [ID] sont symétriques
par rapport à la droite (d’) (le point I est son
propre symétrique).
• [ID] et [IC] sont symétriques par rapport à
la droite (d).
• [IC] et [IB] le sont par rapport à la droite
(d’).
• [IB] et [IA] le sont par rapport à (d).
b) • IA = ID et ID = IC donc IA = IC
IB = IC et IC = ID donc IB = ID
• Comme les points A, I et C sont alignés
ainsi que les points B, I et D, on déduit que I
est le milieu des diagonales.
c) Cette propriété est importante : on devra la
retenir.
© Cned – Académie en ligne

©
Cned, Mathématiques 6e —
21
c
c
Séquence 7
Exercice 32
1)
2%#4!.',%
propriété
propriété
propriété
propriété
propriété
propriété
3IUNQUADRILATÒREESTUNRECTAN
GLEALORSSESDIAGONALESONTLE
MÐME milieu ET LA MÐME
longueur
propriété
propriété
propriété
longueur
propriété
longueur
propriété
longueur
propriété
propriété
propriété
propriété
propriété
2)
2%#4!.',%
propriété
propriété
propriété
3I UN QUADRILATÒRE EST UN
RECTANGLE ALORS SES CÙTÏS
OPPOSÏS ONT la même
longueur
2%#4!.',%
propriété
propriété
propriété
propriété
propriété
propriété
3IUNQUADRILATÒREESTUNRECTAN
GLEALORSSESCÙTÏSOPPOSÏSSONT
parallèles
propriété
propriété
parallèles
propriété
parallèles
propriété
propriété
propriété
propriété
propriété
propriété
propriété
On recopie simplement les mots qui manquent
dans la carte en prenant modèle sur le
paragraphe « JE RETIENS » précédent.
© Cned – Académie en ligne

—
©
Cned, Mathématiques 6e
22
c
c
Séquence 7
Exercice 33
!
7
O
" #
$
• Les diagonales du rectangle ABCD se coupent en O.
• D’après la propriété : « si un quadrilatère est un rectangle
alors ses diagonales ont la même longueur et se coupent en
leur milieu », je peux affirmer que O est le milieu de [AC] et de
[BD], et que AC = BD.
• J’en déduis que : OA = OB = OC = OD
• Le cercle Ω de diamètre [AC] a pour centre le milieu O de
[AC] et son rayon est OA.
Comme OB = OD = OA, B et D appartiennent à Ω.
• Le centre d’un cercle est le milieu de son
diamètre.
• On utilise ici la carte 18 de la Boîte à
Outils.
• Comme O est le milieu de [AC] :
OA = OC = AC ÷ 2
De même, comme O est le milieu de [BD] :
OB = OD = BD ÷ 2
• On utilise la définition du cercle : séquence 1
séance 9 premier paragraphe « JE RETIENS ».
Les distances de B à O et de D à O sont égales
au rayon OA.
Exercice 34
1) 2)
%
&
'
(
!
"
#
$
3) Je n’y arrive pas.
Les commentaires du professeur :
3) On a beau essayer tous les cas de figures, on a toujours l’impression d’avoir un rectangle ...
Par la suite, on va admettre et retenir que ce résultat est toujours vrai, à savoir :
« Si un quadrilatère a ses diagonales qui ont le même milieu et qui ont la même longueur, alors ce quadrilatère est un
rectangle ».
© Cned – Académie en ligne