XII-SYMETRIE AXIALE

6ème-XII-Symétrie axiale 1
{Grec : syn=avec et metron =mesure}
I. SYMETRIE ET PLIAGE ; AXE DE SYMETRIE
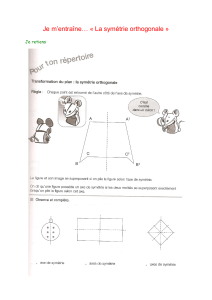
Dans la nature, beaucoup d’animaux ou de cristaux possèdent « un plan de symétrie » : si tu les dessines sur
une feuille, et que tu plies cette feuille suivant une certaine droite, tu remarqueras que les deux parties se
superposent. Cette droite s’appelle un « axe de symétrie »
Définition
Une droite (d) est un axe de symétrie d’une figure si les deux parties de la figure se superposent par
pliage le long de cette droite
II. AXES DE SYMETRIE DES FIGURES USUELLES
 Fiche tri-quad…
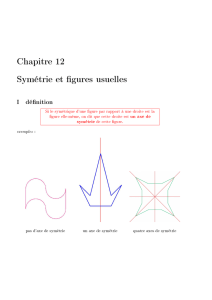
1. le segment
L’axe de symétrie d’un segment est la médiatrice de ce
segment
2. le triangle isocèle
- un triangle isocèle a un axe de symétrie
- l’axe de symétrie d’un triangle isocèle passe par le
sommet principal : c’est la médiatrice du côté opposé au
sommet principal
(c’est aussi la bissectrice de l’angle au sommet principal)
3. le triangle équilatéral
- un triangle équilatéral a trois axes de symétrie : ce sont
les médiatrices des trois côtés du triangle
(ce sont aussi les bissectrices des trois angles)
SYMETRIE AXIALE :
Constructions d’images, conservation, figures symétriques et propriétés
A
B

6ème-XII-Symétrie axiale 2
4. le cerf-volant
- un cerf-volant a un axe de symétrie : c’est une des
diagonales du cerf-volant
5. le losange
- un losange a deux axes de symétrie : ce sont les
diagonales du losange
6. le rectangle
- un rectangle a deux axes de symétrie : ce sont les
médiatrices des côtés du rectangle
7. le carré
- un carré a quatre axes de symétrie : ce sont les
diagonales du carré et les médiatrices des côtés du carré
III. FIGURES SYMETRIQUES
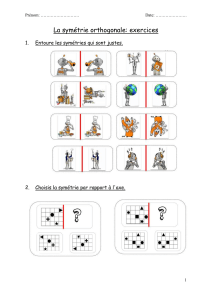
Sur feuille quadrillée, tracer un F majuscule et le même « à l’envers »
Les deux figures se superposent par pliage autour de la droite
(d).
On dit que ces deux figures sont symétriques par rapport à la
droite (d)
1

6ème-XII-Symétrie axiale 3
Définition
Deux figures sont symétriques par rapport à une droite si elles se superposent par pliage autour de
cette droite
Propriété 1
Deux figures symétriques ont la même forme, les mêmes dimensions et la même aire
Propriété 2
Si une figure admet la droite (d) comme axe de symétrie, alors elle est sa propre figure symétrique
par rapport à (d)
Exemple :
IV. POINTS SYMETRIQUES
1. Définition
Deux points distincts A et A’ sont symétriques par
rapport à une droite (d) si (d) est la médiatrice de [AA’]
(et réciproquement)
A
A'
(d)